Основы электротехники и электроники: Курс лекций, страница 18

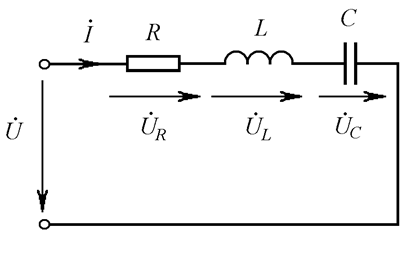
Рис. 22.1

При равенстве фаз входного тока и напряжения выполняется равенство:

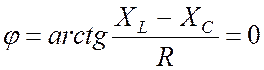                                                               ,       (22.1)

где       – угол между напряжением и током;

 – реактивное сопротивление катушки;

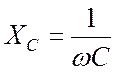             – реактивное сопротивление конденсатора.

Входное сопротивление последовательного колебательного контура в комплексной форме:

                                                               .        (22.2)

Из сравнения (22.1) и (22.2) можно сделать вывод, что в режиме резонанса в цепи с последовательным соединением индуктивности и емкости их реактивные сопротивления равны между собой:

                                                                          ,                   (22.3)

а мнимая часть комплексного входного сопротивления равна нулю:

                                                                        .                 (22.4)

Выражение (22.4) представляет собой основное условие последовательного резонанса. Индекс 0 в (22.3, 22.4) показывает, что значения сопротивлений соответствуют резонансному режиму.

Модуль входного сопротивления определяется как

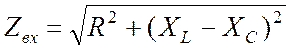                                                            ,     (22.5)

и в режиме последовательного резонанса достигает своего минимального значения:

.

Ток в цепи в режиме последовательного резонанса достигает максимально возможного значения:

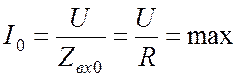                                                                 .         (22.6)

Если активное сопротивление последовательного колебательного контура (Рис. 22.1) стремится к нулю (), то при резонансе он ведет себя как закоротка, а входной ток стремится к бесконечности. В этом случае говорят, что имеет место идеальный последовательный резонанс.

Так как реактивные сопротивления зависят от частоты, резонансную частоту можно определить, приравняв реактивные сопротивления индуктивности и емкости:

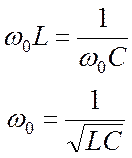                                                                          .                  (22.7)

Из векторной диаграммы (Рис. 22.2) видно, что при последовательном резонансе напряжения на индуктивности и емкости равны по модулю. Именно поэтому последовательный резонанс называют также резонансом напряжений.

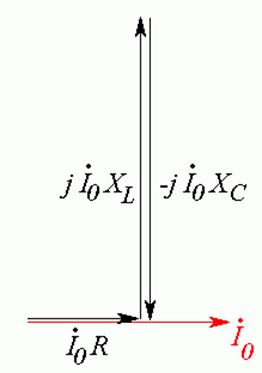
Рис. 22.2

Определим, чему равен модуль напряжения на индуктивности:

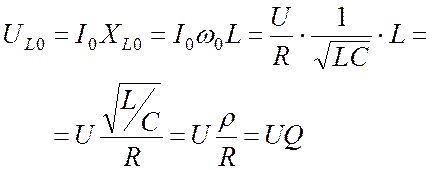                                                 .                                                                                (22.8)

Параметр 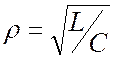 называют волновым или характеристическим сопротивлением резонансного контура, а отношение

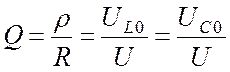                                                                             (22.9)

называют добротностью контура.

Добротность контура (22.9) определяет, во сколько раз напряжение на реактивных элементах больше напряжения на входе при резонансе напряжений.

Добротность резонансного контура может достигать нескольких сотен, и напряжение на реактивных элементах цепи может в сотни раз превышать напряжение на входе.

Предположим, что в контуре (Рис. 22.1) действующее значение входного напряжения, индуктивность, емкость и активное сопротивление остаются постоянными, а частота входного напряжения изменяется в пределах от нуля до бесконечности. Рассмотрим, как будут изменяться действующие значения тока, напряжений на индуктивности и емкости, а также угол между напряжением и током на входе.

Действующее значение тока в цепи как функцию частоты можно представить следующим образом:

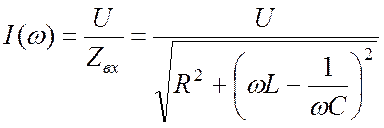                                                     .                                                                               (22.10)

Действующее значение напряжения на индуктивности как функция частоты:

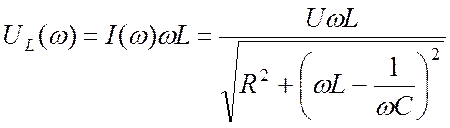                                               .                                                                               (22.11)

Действующее значение напряжения на емкости как функция частоты:

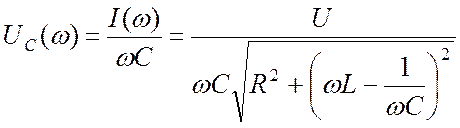                                              .                                                                               (22.12)

Угол между входным напряжением и током как функция частоты:

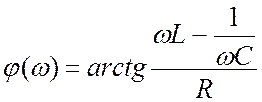                                                               .      (22.13)

Графики функций (22.10-22.13) представлены на Рис. 22.3. Из графиков видно, что напряжения на индуктивности и емкости достигают максимума на частотах, не равных резонансной частоте. При этом неравенство имеет вид:

.

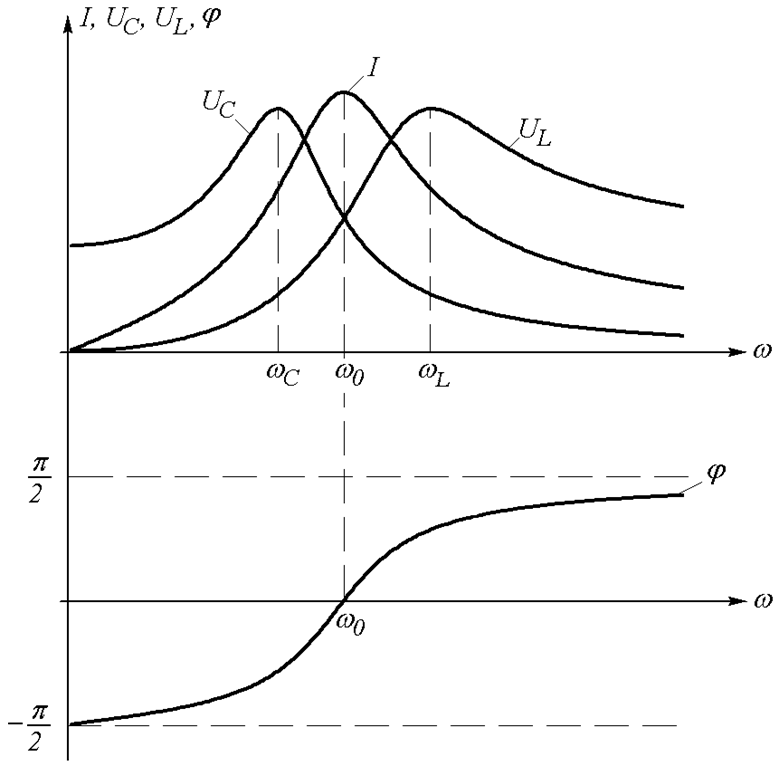
Рис. 22.3

Обычно кривые тока изображают в относительных единицах, выражая частоту в долях резонансной частоты, а ток – в долях тока при резонансе. На Рис. 22.4 изображены кривые тока для различных значений добротности.

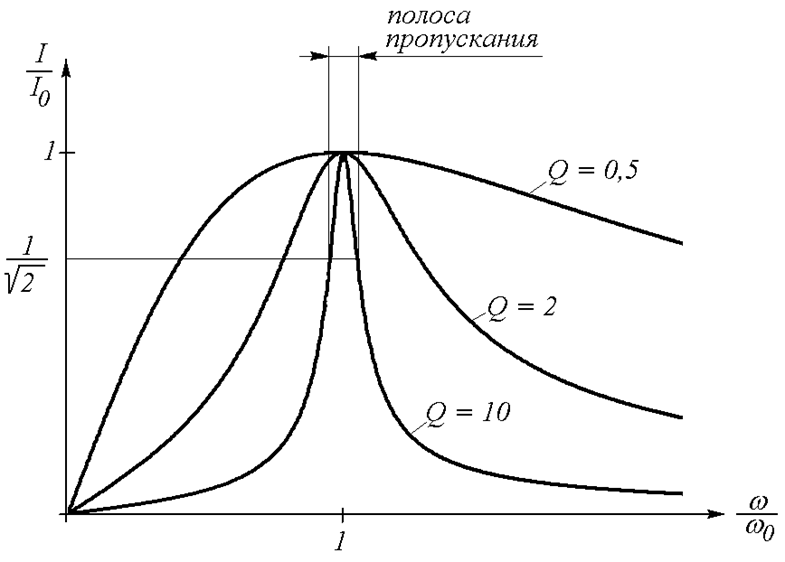
Рис. 22.4

Чем больше добротность, тем более острым становится пик тока и уже полоса пропускания контура. Полосой пропускания резонансного контура называют частотный диапазон, внутри которого отношение  больше, чем .

23. ПАРАЛЛЕЛЬНЫЙ РЕЗОНАНС (РЕЗОНАНС ТОКОВ)

Рассмотрим цепь с параллельным соединением резистора, индуктивной катушки и конденсатора (Рис. 23.1). Такую цепь назовем параллельным колебательным контуром.

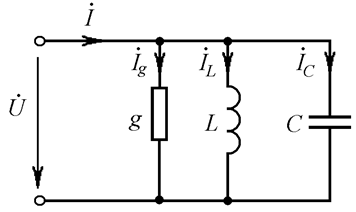
Рис. 23.1

В резонансном режиме такая цепь также ведет себя как активный элемент. Здесь также разность фаз между током и напряжением на входе при резонансе равна нулю, то есть

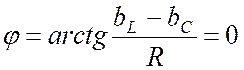                                                                ,         (23.1)

где       – угол между напряжением и током;

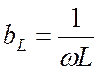 – реактивная проводимость катушки;

             – реактивная проводимость конденсатора.

Входная проводимость параллельного колебательного контура в комплексной форме:

                                                                  .          (23.2)

Из сравнения (23.1) и (23.2) видно, что в режиме резонанса в цепи с параллельным соединением индуктивности и емкости их реактивные проводимости равны между собой:

                                                                            ,                     (23.3)

а мнимая часть комплексной входной проводимости равна нулю:

                                                                        .                 (23.4)