Произведем проверку расчета токов с помощью баланса мощности. При расчете мощности источников токи мы должны направить так, чтобы они совпадали с направлением ЭДС (См. Рис. 8.2). Итак, мощность источников:
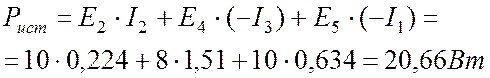 .
.
Мощность потребителей:
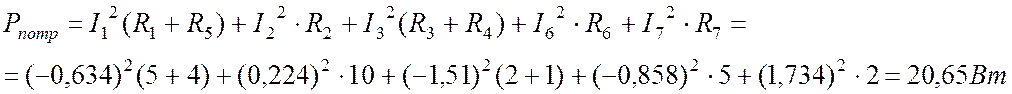 .
.
С учетом
вычислительных погрешностей ![]() .
.
Общий вид системы уравнений метода контурных токов:
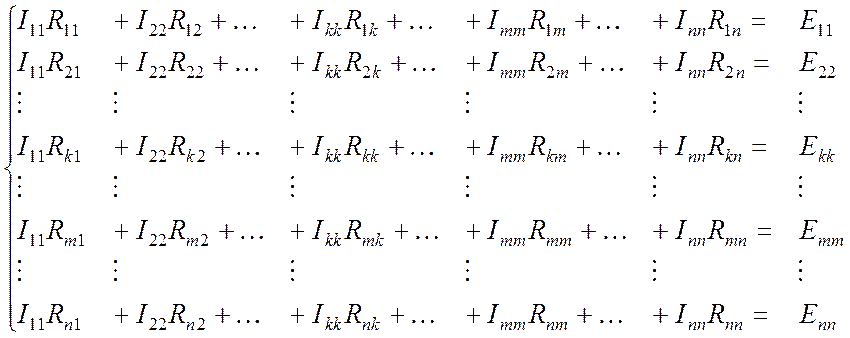
![]() , (8.7)
, (8.7)
где ![]() называется
собственным или полным сопротивлением контура. Оно равно сумме всех сопротивлений
контура и всегда положительно.
называется
собственным или полным сопротивлением контура. Оно равно сумме всех сопротивлений
контура и всегда положительно.
![]() называется
сопротивлением смежной ветви. Если контурные токи в смежной ветви встречны,
называется
сопротивлением смежной ветви. Если контурные токи в смежной ветви встречны, ![]() . Если контурные токи в смежной ветви
одного направления,
. Если контурные токи в смежной ветви
одного направления, ![]() . И при этом всегда
справедливо равенство
. И при этом всегда
справедливо равенство ![]() .
.
![]() называется
контурной ЭДС. Контурная ЭДС равна алгебраической сумме отдельных ЭДС контура.
называется
контурной ЭДС. Контурная ЭДС равна алгебраической сумме отдельных ЭДС контура.
Главный определитель системы (8.7) имеет вид:
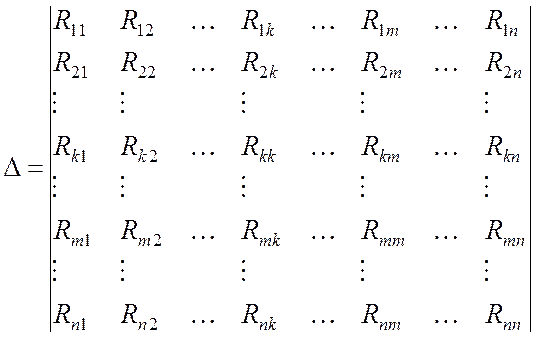
![]() . (8.8)
. (8.8)
Он всегда симметричен относительно главной диагонали.
Чтобы решить систему (8.7) методом Крамера, необходимо найти алгебраические дополнения определителя (8.8).
Алгебраическое дополнение Δkm определителя (8.8) можно получить путем вычеркивания из определителя (8.8) k-го столбца и m-ой строки и умножения полученного определителя на (‑1)k+m
Решая систему (8.7) в общем виде, получим для любого k-го контурного тока выражение:
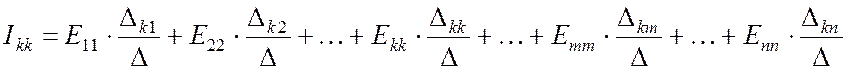 . (8.9)
. (8.9)
Выражение (8.9) имеет важное теоретическое значение и будет использоваться в дальнейшем при рассмотрении методов расчета электрических цепей.
Особенности метода контурных токов при наличии в цепи источников тока
При наличии в схеме источника тока записать уравнение по второму закону Кирхгофа для контура с источником нельзя. Однако, расчетные контуры можно выбрать так, чтобы каждый источник тока входил только в один независимый контур. Тогда реальный ток источника будет равен контурному току, и, следовательно, этот контурный ток уже будет известен. Для него не надо записывать уравнения по второму закону Кирхгофа. Но он будет входить в уравнения для других контурных токов. При формировании системы уравнений его необходимо перенести в правую часть системы как известную величину.
Пример 8.2:
Найти неизвестные токи методом контурных токов (Рис. 8.3).
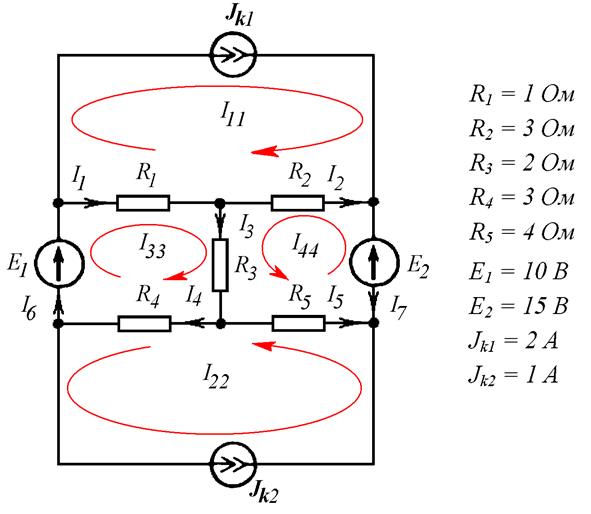
Рис. 8.3
В схеме четыре независимых контура. Выбираем контуры так, чтобы каждый источник тока входил только в один контур и ток источника был равен контурному. В данном случае:
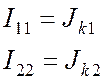 .
.
Составляем систему уравнений для контурных токов I33 и I44:
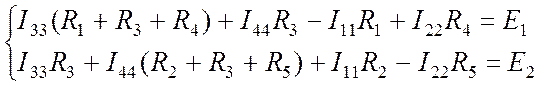 . (Пр.
8.2.1)
. (Пр.
8.2.1)
Преобразуем систему (Пр. 8.2.1), перенеся в правую часть слагаемые, содержащие известные величины:
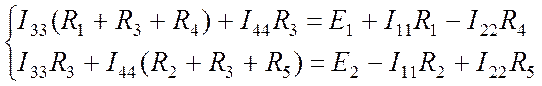 . (Пр.
8.2.2)
. (Пр.
8.2.2)
Подставляем в систему (Пр. 8.2.2) числа:
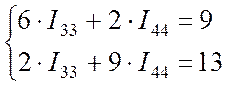 . (Пр. 8.2.3)
. (Пр. 8.2.3)
Систему (Пр. 8.2.3) решаем методом Крамера:
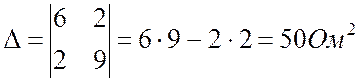 .
.
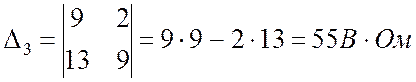 .
.
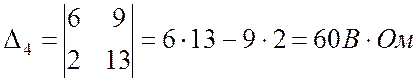 .
.
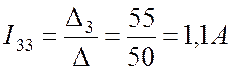 .
.
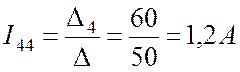
Вычисляем реальные токи через контурные (См. Рис. 8.3):
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
Произведем проверку расчета токов с помощью баланса мощности. Токи в ветвях с ЭДС направим так, чтобы они совпадали с направлением ЭДС, напряжения на выводах источников тока направим противоположно току источников (Рис. 8.4).
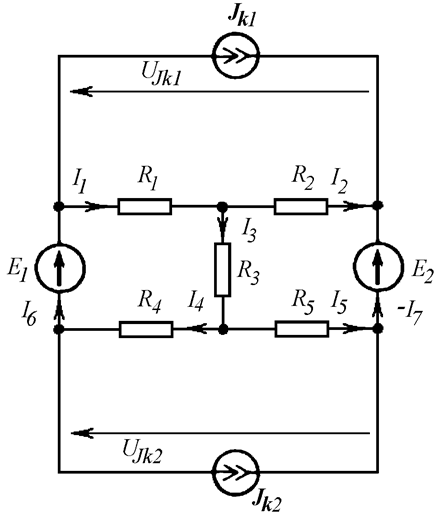
Рис. 8.4
Напряжения на выводах источников тока:
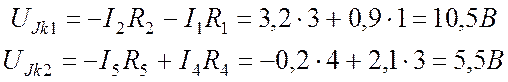 .
.
Мощность источников:
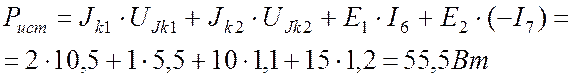 .
.
Мощность потребителей:
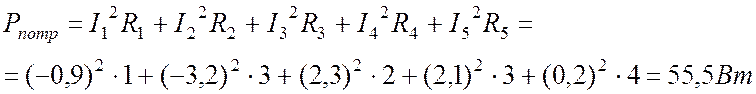 .
.
Мощность источников равна мощности потребителей:
![]() .
.
9. МЕТОД НАЛОЖЕНИЯ
При рациональном выборе контуров всегда можно добиться того, чтобы ветвь с искомым током входила только в один независимый контур. Тогда реальный ток будет совпадать с контурным, и для него будет справедливо соотношение (8.9):
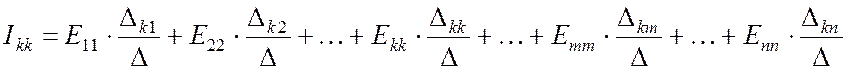 .
.
Каждую из контурных ЭДС можно выразить через ЭДС ветвей E1, E2, E3…
Тогда соотношение (8.9) предстанет в виде:
![]() . (9.1)
. (9.1)
Очевидно, что в выражении (9.1) каждое слагаемое представляет собой часть полного тока, обусловленную лишь одной ЭДС.
Отсюда следует важный в теоретическом отношении вывод: ток в произвольной ветви равен алгебраической сумме частичных токов, порождаемых каждым из источников в отдельности.
На этом принципе основан расчетный метод, называемый методом наложения.
Алгоритм расчета цепи методом наложения
Поочередно рассчитываются токи, возникающие от действия каждого источника в отдельности. При этом остальные источники мысленно удаляются из цепи, но сохраняются их внутренние сопротивления. Истинный ток определяется алгебраической суммой частичных токов.
Пример 9.1:
Найти неизвестные токи методом наложения (Рис. 9.1).
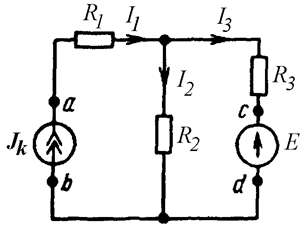
Рис. 9.1
В схеме два источника. Разбиваем исходную схему на две: схему с источником тока и схему с источником ЭДС.
Находим составляющие токов, создаваемых источником тока. Для этого удаляем из схемы источник ЭДС. Так как внутреннее сопротивление источника ЭДС равно нулю, на его место (между точками c и d) ставим закоротку (Рис. 9.2).
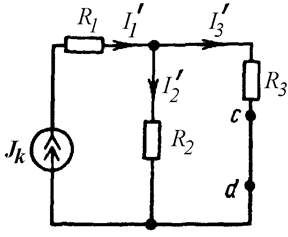
Рис. 9.2
Не вызывает
сомнений, что ток ![]() равен току источника:
равен току источника:
![]() .
.
Для
определения токов ![]() и
и ![]() воспользуемся
так называемым правилом параллельного разброса, которое состоит в следующем.
Пусть в узел a втекает известный ток I (Рис. 9.3). Необходимо найти токи
воспользуемся
так называемым правилом параллельного разброса, которое состоит в следующем.
Пусть в узел a втекает известный ток I (Рис. 9.3). Необходимо найти токи ![]() и
и ![]() .
.
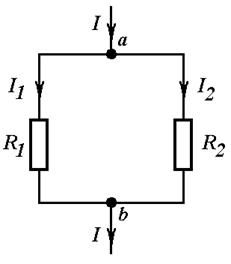
Рис. 9.3
Запишем эквивалентное сопротивление двух параллельных ветвей:
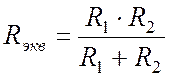 . (Пр. 9.1.1)
. (Пр. 9.1.1)
Теперь, чтобы
найти ток ![]() , протекающий через резистор
, протекающий через резистор ![]() (см. Рис. 9.3), в
формулу эквивалентного сопротивления (Пр. 9.1.1) вместо
(см. Рис. 9.3), в
формулу эквивалентного сопротивления (Пр. 9.1.1) вместо ![]() в числителе ставим ток I, втекающий в узел a:
в числителе ставим ток I, втекающий в узел a:
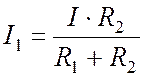 .
.
Аналогично
находится ток ![]() через резистор
через резистор ![]() :
:
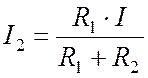 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.