Вернемся к схеме на Рис. 9.2. Здесь эквивалентное сопротивление двух параллельных ветвей:
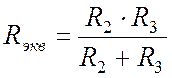 .
.
Ток, втекающий
в узел, – это, несомненно, ![]() . Согласно правилу
параллельного разброса:
. Согласно правилу
параллельного разброса:
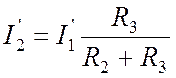 .
.
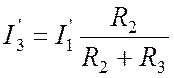 .
.
Теперь находим составляющие токов, создаваемых источником ЭДС. Для этого удаляем из схемы источник тока. Так как внутреннее сопротивление источника тока бесконечно велико, на его месте (между точками a и b) оставляем разрыв (Рис. 9.4).
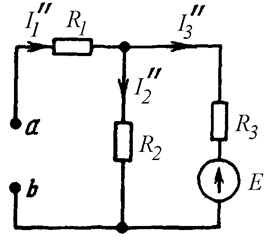
Рис. 9.4
Цепь на Рис. 9.4 – это одноконтурная цепь. Здесь
![]() ,
,
![]() .
.
С другой
стороны, ток ![]() можно
найти по закону Ома:
можно
найти по закону Ома:
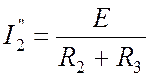 .
.
Наконец, находим реальные токи (см. Рис. 9.1):
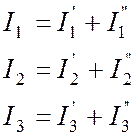 .
.
Метод наложения не может использоваться для расчета мощности, поскольку мощность пропорциональна не току, а квадрату тока.
Заметим также, что метод наложения применим только к линейным цепям.
10. ПРЕОБРАЗОВАНИЕ ЗВЕЗДЫ В ТРЕУГОЛЬНИК И ТРЕУГОЛЬНИКА В ЗВЕЗДУ
Соединение трех сопротивлений, имеющее вид трехлучевой звезды (Рис. 10.1а), называют звездой, а соединение трех сопротивлений, при котором они образуют стороны треугольника (Рис. 10.1б), называют треугольником. В узлах 1, 2, 3 звезда и треугольник соединяются с остальной частью схемы (не показанной на рисунках).
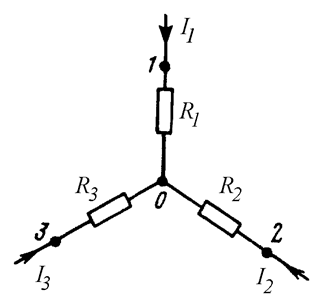
а)

б)
Рис. 10.1
Токи,
подтекающие к узлам 1, 2, 3, имеют обозначения 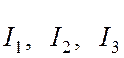 .
Потенциалы узлов 1, 2 и 3 –
.
Потенциалы узлов 1, 2 и 3 – 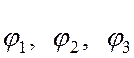 .
.
Часто при расчетах электрических цепей необходимо преобразовывать треугольник в звезду или звезду в треугольник. Если преобразование выполнить таким образом, что потенциалы узлов 1, 2, 3 и токи, подтекающие к этим узлам, останутся неизменными, то вся внешняя схема «не заметит» произведенной замены. Формулы преобразований получим из законов Ома и Кирхгофа.
Для звезды по первому закону Кирхгофа:
![]() . (10.1)
. (10.1)
Здесь и далее
знак ![]() над током означает, что формула
относится к звезде.
над током означает, что формула
относится к звезде.
Но, с другой стороны, из закона Ома получаем соотношения:
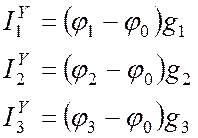 . (10.2)
. (10.2)
Подставим
(10.2) в (10.1) и найдем ![]() :
:
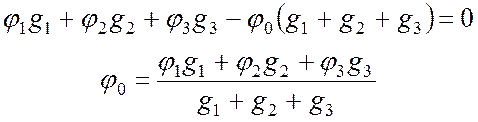 . (10.3)
. (10.3)
Так как в
треугольнике нет узла 0, исключим потенциал этого узла из соотношений
(10.2). Для этого подставляем (10.3) в (10.2) и, в частности, для тока ![]() получим выражение:
получим выражение:
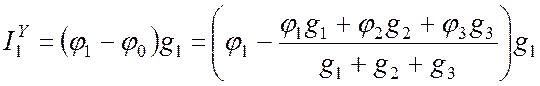 . (10.4)
. (10.4)
Для треугольника по первому закону Кирхгофа:
![]() . (10.5)
. (10.5)
Здесь и далее
знак ![]() над током означает, что формула
относится к треугольнику.
над током означает, что формула
относится к треугольнику.
Так как токи,
подтекающие извне к звезде и треугольнику, равны, приравняем ![]() и
и ![]() из
(10.4) и (10.5). Проделаем эту операцию и для других токов и после
преобразований получим:
из
(10.4) и (10.5). Проделаем эту операцию и для других токов и после
преобразований получим:
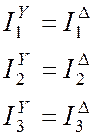 ,
,
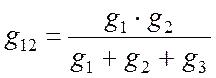 , (10.6)
, (10.6)
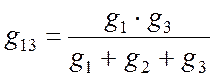 , (10.7)
, (10.7)
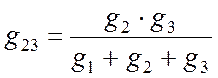 . (10.8)
. (10.8)
Из выражений (10.6-10.8) получаются формулы сопротивлений при преобразовании звезды в треугольник:
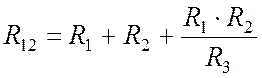 , (10.9)
, (10.9)
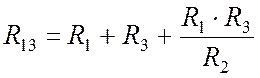 , (10.10)
, (10.10)
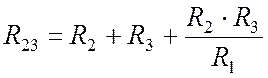 . (10.11)
. (10.11)
Из полученных формул выводятся обратные, для преобразования треугольника в звезду:
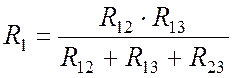 , (10.12)
, (10.12)
 , (10.13)
, (10.13)
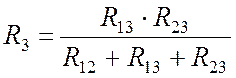 . (10.14)
. (10.14)
Чтобы запомнить и правильно использовать формулы (10.9-10.14), можно порекомендовать следующий прием.
При преобразовании звезды в треугольник установить два пальца в те узлы, к которым будет подсоединяться ветвь треугольника. Искомое сопротивление ветви треугольника будет равно сумме сопротивлений лучей звезды, подходящих к пальцам, плюс произведение этих сопротивлений, деленное на сопротивление оставшегося луча.
При преобразовании треугольника в звезду установить один палец в тот узел, к которому будет подсоединяться луч звезды. Искомое сопротивление луча звезды – это произведение сопротивлений ветвей, подходящих к пальцу, деленное на сумму сопротивлений всех трех ветвей треугольника.
Если сопротивления всех ветвей звезды или треугольника равны, такие звезда и треугольник называются симметричными. Сопротивления ветвей эквивалентных симметричных звезды и треугольника связаны соотношением, которое можно вывести из (10.9-10.14):
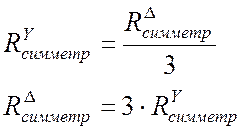 .
.
Пример 10.1:
Решить задачу (Рис. 10.2).
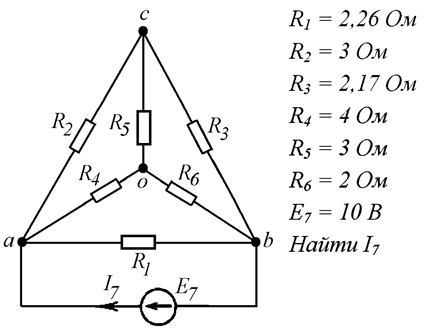
Рис. 10.2
Преобразуем звезду R4, R5, R6 в эквивалентный треугольник Rab, Rbc, Rac (Рис. 10.3).
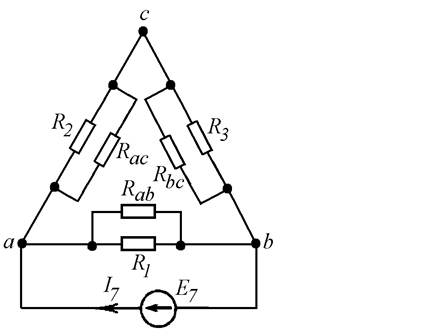
Рис. 10.3
Рассчитываем параметры треугольника:
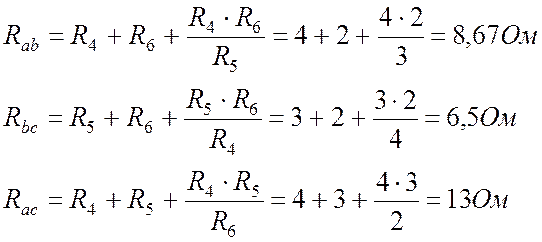 .
.
Сворачиваем сопротивления параллельных ветвей:
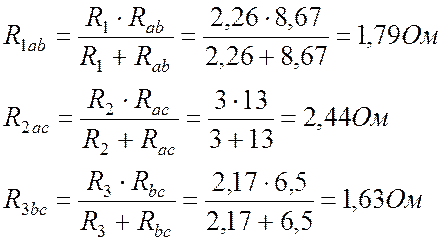 .
.
Сворачиваем все сопротивления в одно эквивалентное:
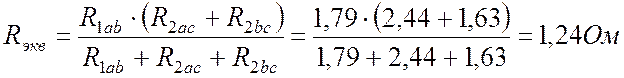 .
.
Находим ток ![]() по закону Ома:
по закону Ома:
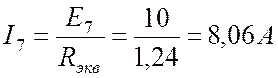 .
.
11. СВЕРТКА ПАРАЛЛЕЛЬНЫХ ВЕТВЕЙ В ОДНУ ЭКВИВАЛЕНТНУЮ
Пусть несколько параллельных ветвей (с источниками и без) располагаются между ветвями a и b (Рис. 11.1 а). При этом извне в узел a втекает ток I, а из узла b этот же ток вытекает. Заменим эти параллельные ветви одной эквивалентной, содержащей ЭДС Eэкв и сопротивление Rэкв (Рис. 11.1 б).
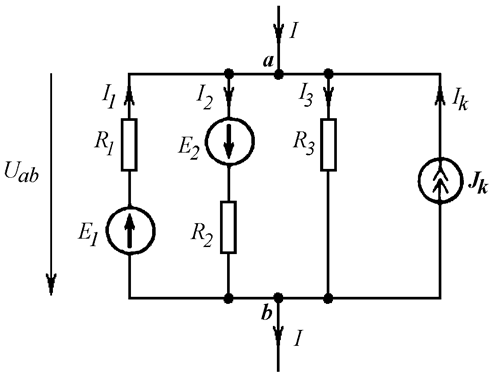
а)
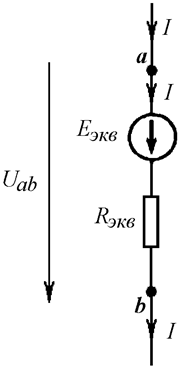
б)
Рис. 11.1
Для этого запишем уравнения по первому закону Кирхгофа и закону Ома для параллельных ветвей:
![]()
![]() , (11.1)
, (11.1)
![]() , (11.2)
, (11.2)
![]() , (11.3)
, (11.3)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.