Электротехника \ Основы электротехники и электроники

Основы электротехники и электроники: Курс лекций, страница 24

Нелинейные магнитные свойства ферромагнетика задают с помощью основной кривой намагничивания – зависимости индукции от напряженности магнитного поля, представленной в табличном или графическом виде (Рис. 27.1).

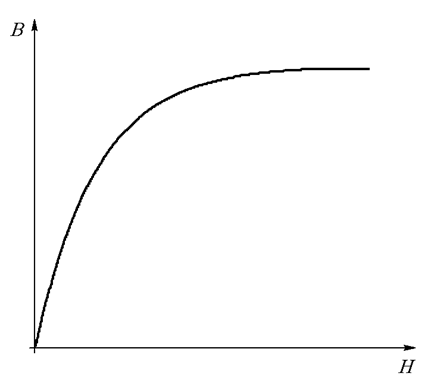
Рис. 27.1

Рассмотрим некоторую магнитную цепь, состоящую из замкнутого ферромагнитного сердечника, на который намотана катушка, содержащая W витков. По катушке течет неизменный во времени ток I (Рис. 27.2 а). Магнитные свойства сердечника заданы кривой намагничивания (Рис. 27.2 б). Геометрия системы известна.

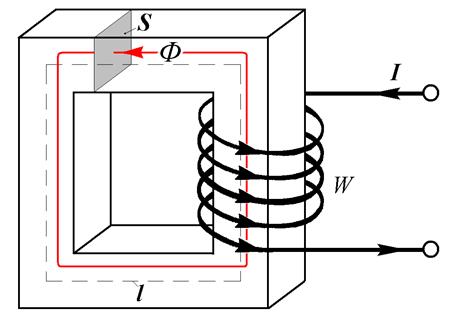
а)

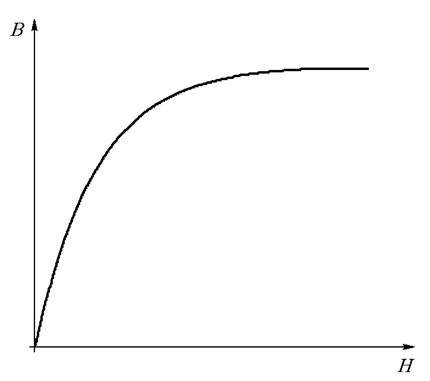
б)

Рис. 27.2

Источником магнитного поля в цепи является магнитодвижущая сила (МДС), определяемая как произведение числа витков катушки на протекающий по катушке ток:

                                                                           .                    (27.2)

Магнитодвижущая сила (МДС) является аналогом известной нам электродвижущей силы (ЭДС) и обозначается на схемах замещения аналогично ЭДС (Рис. 27.3). Размерность МДС – амперы.

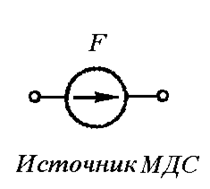
Рис. 27.3

МДС создает в сердечнике замкнутый магнитный поток  (греческая буква фи). Направление магнитного потока в сердечнике определяется правилом правой руки. Правой рукой надо обхватить катушку так, чтобы четыре пальца были направлены в ту же сторону, что и ток в катушке. Тогда большой палец укажет направление магнитного потока. Магнитный поток является аналогом электрического тока. Единица магнитного потока – Вебер (Вб).

Требуется рассчитать магнитный поток в сердечнике при заданной МДС.

Наконец, в схеме замещения должен быть потребитель. Это нелинейное магнитное сопротивление RM, моделирующее реакцию ферромагнитного сердечника на магнитное поле в нем. В окончательном виде схема замещения выглядит так, как показано на Рис. 27.4. В этой схеме один контур, так как магнитный поток в сердечнике не разветвляется. МДС источника уравновешивается падением магнитного напряжения UM на нелинейном магнитном сопротивлении.

Обратить внимание! Размерность магнитного напряжения и МДС – амперы (ни в коем случае не вольты!).


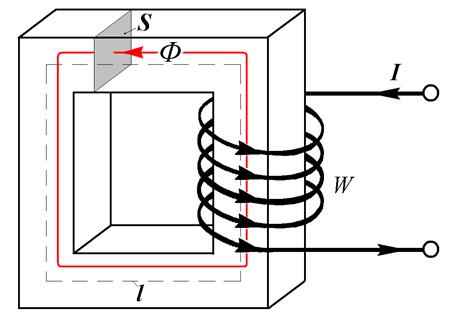
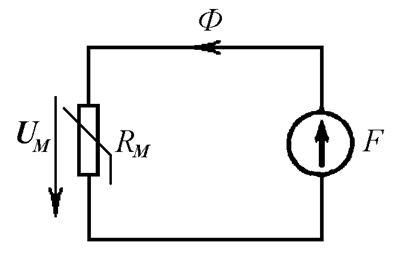
Рис. 27.4

Так как нелинейное магнитное сопротивление RM моделирует в схеме замещения ферромагнитный сердечник, магнитное напряжение UM связано с напряженностью магнитного поля в сердечнике:

                                                                          ,                   (27.3)

где       –      длина средней линии сердечника в направлении потока; иными словами, это путь,

                        который преодолевает магнитный поток в сердечнике.

Магнитный поток связан с индукцией магнитного поля в сердечнике следующей зависимостью:

                                                                           ,                    (27.4)

где       –     площадь поперечного сечения сердечника в направлении перпендикулярном,

                        направлению магнитного потока.

Ни индукция, ни напряженность магнитного поля нам пока неизвестны. Но анализ задачи показывает, что к ней можно применить те же принципы, на которых основываются расчеты нелинейных цепей постоянного тока.

Рассмотрим кривую намагничивания ферромагнитного сердечника (Рис. 27.2 б). По оси абсцисс здесь отложена напряженность магнитного поля. Если абсциссу текущей точки графика умножить на длину средней линии сердечника, получим значение магнитного напряжения в текущей точке (27.3).

По оси ординат отложена индукция магнитного поля. Если ординату текущей точки графика умножить на площадь поперечного сечения сердечника, получим значение магнитного потока в текущей точке (27.4).

Таким образом, можно получить так называемую вебер-амперную характеристику нелинейного магнитного элемента (Рис. 27.5).

Для магнитной цепи справедлив второй закон Кирхгофа: сумма падений магнитных напряжений в замкнутом контуре равна сумме МДС, включенных в контур. В данном случае:

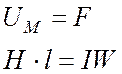                                                                          .                   (27.5)

На оси абсцисс откладываем значение МДС, вычисленное по выражению (27.2). На вебер-амперной характеристике находим рабочую точку. Ордината этой точки – это искомый магнитный поток в сердечнике. Задача решена.


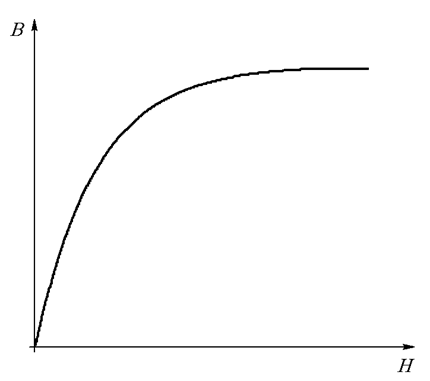
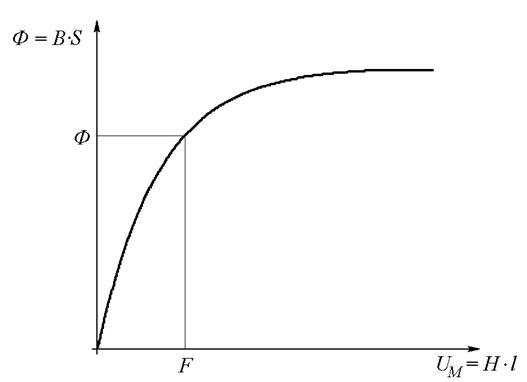
Рис. 27.5

Усложним только что решенную задачу. Пусть теперь в сердечнике пропилен воздушный зазор шириной δ (Рис. 27.6 а). При этом длина средней линии сердечника стала меньше. Для упрощения дальнейших рассуждений будем считать, что площадь поперечного сечения воздушного зазора равна площади сечения сердечника. Магнитные свойства сердечника по-прежнему заданы кривой намагничивания (Рис. 27.6 б). Требуется рассчитать магнитный поток в воздушном зазоре при заданной МДС катушки.

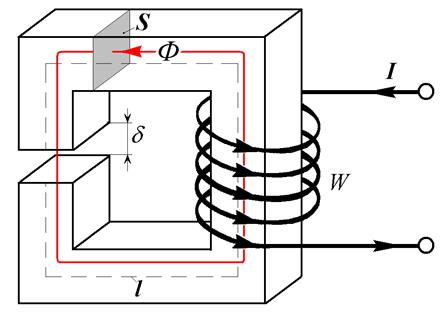
а)

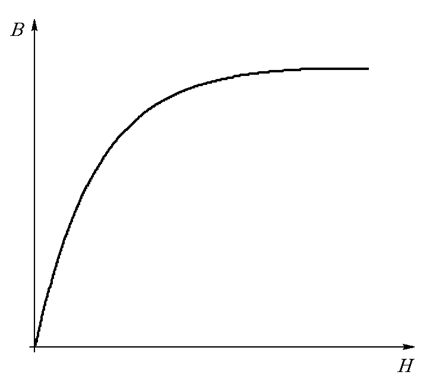
б)

Рис. 27.6

В схеме замещения магнитной цепи, как и в предыдущей задаче, будет один контур, так как магнитный поток не разветвляется. Также, в силу известного принципа непрерывности магнитного потока, поток при выходе из незамкнутого сердечника и входе в зазор не может измениться скачком. Значит и в сердечнике, и в зазоре будет один и тот же магнитный поток. Сердечник будет моделироваться нелинейным магнитным сопротивлением RM. Но кроме сердечника сопротивление магнитному потоку оказывает и воздушный зазор. Индукция в воздушном зазоре связана с магнитной напряженностью в зазоре следующей зависимостью:

                                                                          .                   (27.6)


Левую часть уравнения (27.6) умножим и разделим на площадь поперечного сечения зазора . Правую часть уравнения (27.6) умножим и разделим на ширину зазора δ:

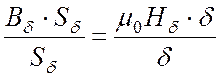                                                                  .           (27.7)

Произведение  в правой части уравнения (27.7) – это падение магнитного напряжения в зазоре (ср. с выражением (27.3)). Произведение  в левой части уравнения (27.7) – это магнитный поток в зазоре, а значит и в сердечнике (ср. с выражением (27.4)). Преобразуя (27.7), получаем зависимость между магнитным потоком и магнитным напряжением в зазоре. Это линейная функция:

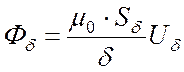                                                                     .              (27.8)

Выражение 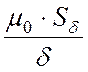 в (27.8) называют магнитной проводимостью воздушного зазора и обозначают греческой буквой лямбда:

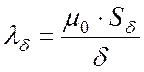                                                                         .                 (27.9)

Размерность магнитной проводимости – Генри (Гн).

Так как функция (27.8) линейна, воздушный зазор в схеме замещения будет моделироваться линейным магнитным сопротивлением Rδ. Схема замещения магнитной цепи представлена на Рис. 27.7.

Скачать файл