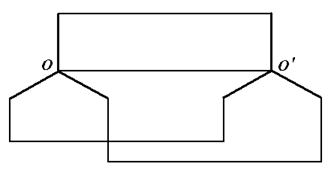
Электротехника \ Основы электротехники и электроники

Основы электротехники и электроники: Курс лекций, страница 21


а) Y-Y с нулевым проводом

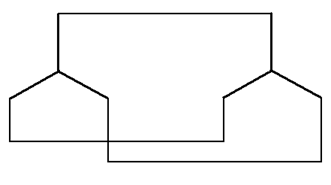
б) Y-Y без нулевого провода


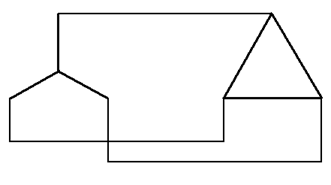
в) Y-Δ

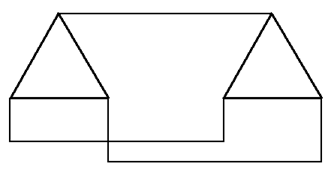
г) Δ-Δ


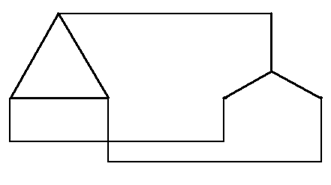
д) Δ-Y

Рис. 25.4

Так как и источники, и потребители можно соединять звездой и треугольником, возможны пять схем трехфазных цепей (Рис. 25.4):

а)  звезда-звезда с нулевым проводом; нулевой провод соединяет центры звезд;

б)  звезда-звезда без нулевого провода;

в)  звезда-треугольник;

г)  треугольник-треугольник;

д)  треугольник-звезда.

Схемы обозначаются Y-Y, Y-Δ, Δ-Δ, Δ-Y.

Выводы трехфазного генератора обозначают прописными латинскими буквами A, B, C (Рис. 25.5).

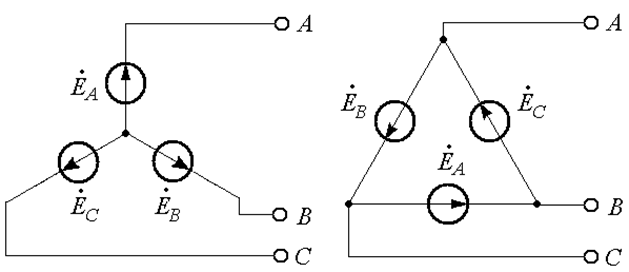
Рис. 25.5


В том случае, если ЭДС генератора соединены звездой, центр звезды называют нулевой точкой генератора и обозначают O (Рис. 25.6 а).

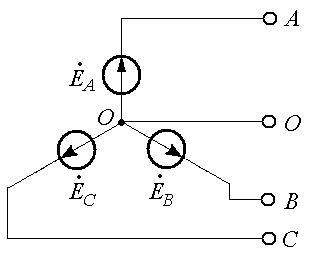
а)

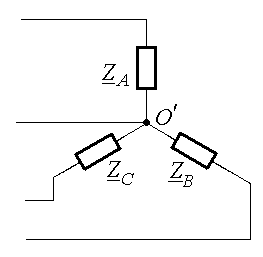
б)

Рис. 25.6

Если звездой соединены сопротивления нагрузки, центр этой звезды называют нулевой точкой нагрузки O’ (Рис. 25.6 б). Нулевым проводом называют провод, соединяющий нулевые точки генератора и нагрузки. Ток в нулевом проводе обозначается I0.

Провода, соединяющие генератор и нагрузку, называют линейными, токи в них – линейными токами IA, IB, IC, напряжения между линейными проводами называют линейными напряжениями UAB, UBC, UCA (Рис. 25.7).

Каждую из трех ЭДС генератора называют фазой генератора, каждое из трех сопротивлений нагрузки называют фазой нагрузки. Токи в фазах называют фазными токами, напряжения на фазах называют фазными напряжениями (Рис. 25.7). Как видно из Рис. 25.7, в звезде фазные токи равны линейным.

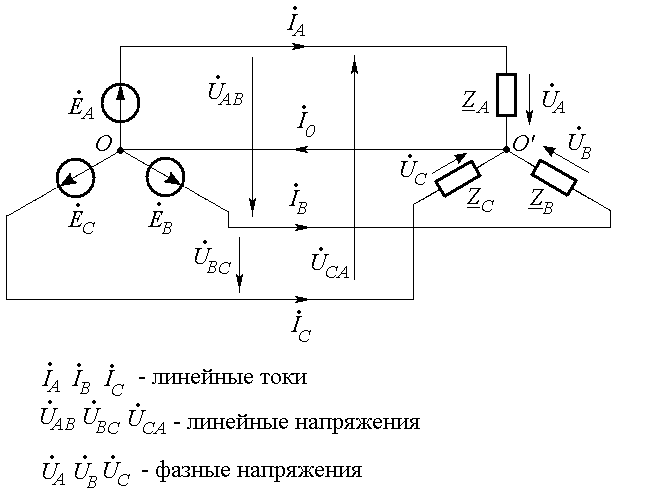
Рис. 25.7


Как видно из Рис. 25.8, в треугольнике фазные напряжения равны линейным.

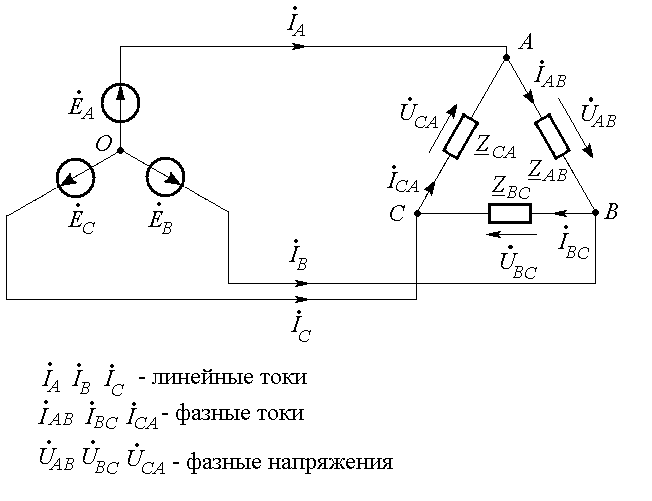
Рис. 25.8

Рассмотрим трехфазный генератор, собранный по схеме Y, в режиме холостого хода. На его зажимах имеются линейные и фазные напряжения (Рис. 25.9).

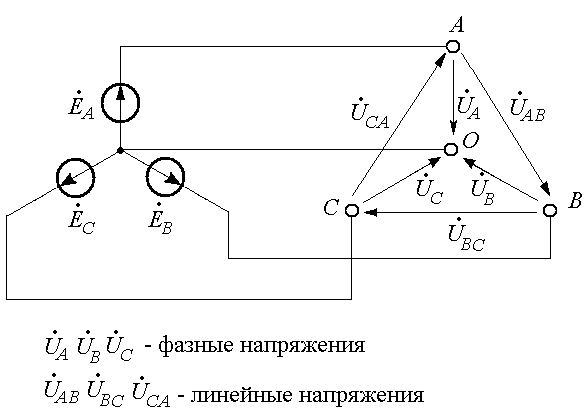
Рис. 25.9

Из второго закона Кирхгофа выведем соотношения между ЭДС и напряжениями на зажимах генератора.

В случае фазных напряжений второй закон Кирхгофа обращается в тривиальные равенства:

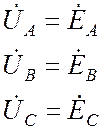                                                                            .                     (25.1)


Для линейных напряжений система уравнений имеет вид:

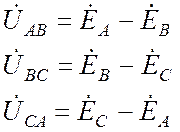                                                                      .              (25.2)

Подставим (25.1) в (25.2):

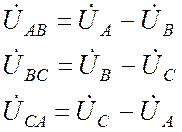                                                                     .              (25.3)

Система уравнений (25.3) позволяет построить векторную диаграмму (Рис. 25.10). Здесь фазные напряжения образуют звезду, которая тождественна звезде ЭДС. Линейные напряжения образуют треугольник, описанный около звезды.

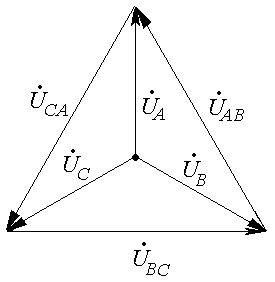
Рис. 25.10

С помощью векторной диаграммы найдем соотношения между действующими значениями фазных и линейных напряжений. Например, действующее значение линейного напряжения между фазами  и  – это модуль вектора . По теореме косинусов (квадрат любой стороны треугольника равен сумме квадратов двух других сторон без их удвоенного произведения на косинус угла между ними):

                                                  .                                                                                (25.4)

Действующие значения всех фазных напряжений равны между собой, обозначим их . Действующие значения всех линейных напряжений также равны между собой, обозначим их . Следовательно, (25.4) можно записать так:

                              .                                                                                (25.5)

Так как 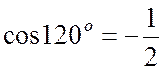, (25.5) примет вид:

                                                                          ,                  (25.6)

откуда

                                                                        .                 (25.7)

Соотношение (25.7) – одно из фундаментальных соотношений в теории трехфазных цепей. В схеме Y линейное напряжение больше фазного в  раз. В основу формирования ряда трехфазных напряжений положен . Каждое последующее напряжение ряда больше предыдущего в  раз:

… 127, 220, 380, 660 В…

Режимы трехфазной цепи

Основным режимом работы трехфазной цепи является симметричный режим. В этом режиме к симметричной системе ЭДС подключается симметричная нагрузка – три совершенно одинаковых сопротивления. Они могут быть чисто активными, чисто реактивными или активно-реактивными.

Векторная диаграмма системы симметричных ЭДС всегда представляет собой симметричную звезду (если ЭДС соединены в треугольник, треугольник векторов всегда может быть перестроен в звезду). В этом случае токи в симметричной нагрузке также будут изображаться симметричной звездой векторов, смещенной относительно звезды ЭДС на угол  (Рис. 25.11). О физической природе угла  говорилось в §19 «МОЩНОСТЬ СИНУСОИДАЛЬНОГО РЕЖИМА».

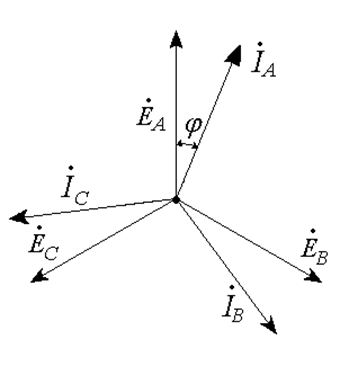
Рис. 25.11

Свойство симметрии позволяет рассчитывать симметричный режим только на одну фазу, например, фазу A, как будто остальных фаз не существует. Когда определены напряжения и токи в фазе A, напряжения и токи в фазах B и C определяются поворотом соответствующих векторов на ‑120О и +120О.

Определенный интерес представляет вопрос о симметрии нагрузки в схемах Y-Y.

Рассмотрим вначале схему «Y-Y с нулевым проводом» (Рис. 25.12 а).

Уравнение по первому закону Кирхгофа в этой схеме имеет вид:

                                                                 .         (25.8)

Вместе с тем, в симметричном режиме фазные токи, образуя симметричную звезду, в сумме дают ноль:

                                                                     .              (25.9)

Сравнивая (25.8) и (25.9), приходим к выводу, что в симметричном режиме ток нулевого провода равен нулю. Следовательно, в симметричном режиме нулевой провод не требуется.


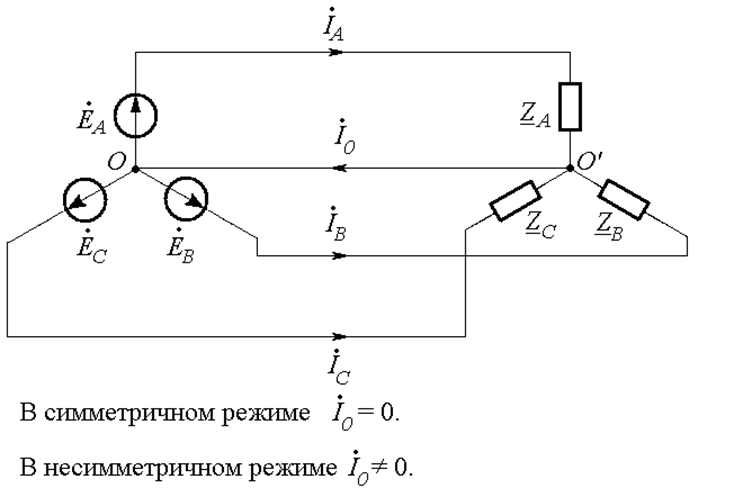
а)

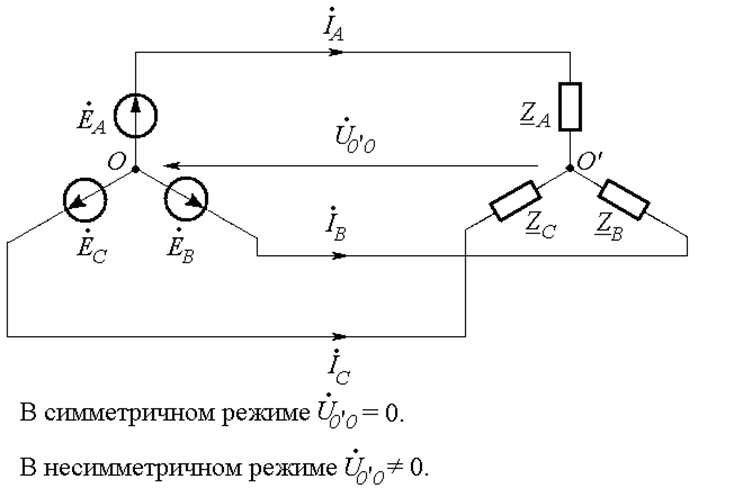
б)

Рис. 25.12

Но как только в нагрузке появляется несимметрия (сопротивления нагрузки по каким-то причинам перестают быть совершенно одинаковыми), условие (25.9) перестает выполняться, фазные токи в сумме уже не дают ноль, и в нулевом проводе появляется ток.

Скачать файл