Основы электротехники и электроники: Курс лекций, страница 19

Выражение (23.4) представляет собой основное условие параллельного резонанса.

Модуль входной проводимости

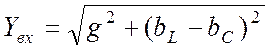                                                                      (23.5)

в режиме параллельного резонанса достигает своего минимального значения:

.

Входной ток в режиме параллельного резонанса достигает минимально возможного значения:

                                                           .    (23.6)

Если активная проводимость параллельного колебательного контура (Рис. 23.1) стремится к нулю (, резистор отсутствует), то в режиме резонанса контур ведет себя как разрыв, а входной ток стремится к нулю. В этом случае говорят, что имеет место идеальный параллельный резонанс.

Так как реактивные проводимости зависят от частоты, резонансную частоту можно определить, приравняв реактивные проводимости индуктивности и емкости:

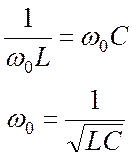                                                                          .                  (23.7)

Из векторной диаграммы (Рис. 23.2) видно, что при параллельном резонансе токи в индуктивности и емкости равны по модулю. Именно поэтому параллельный резонанс называют также резонансом токов.

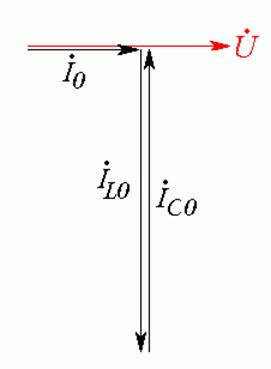
Рис. 23.2

Определим, чему равен модуль тока в индуктивности:

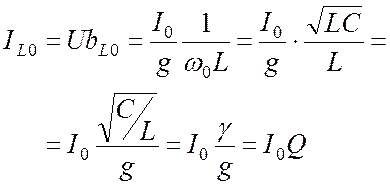                                                    .                                                                                (23.8)

Параметр 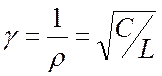 называют волновой или характеристической проводимостью резонансного контура, а отношение

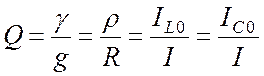                                                                       (23.9)

так же, как и в случае резонанса напряжений – это добротность контура.

Из выражения (23.9) видно, что при резонансе токов добротность контура определяет, во сколько раз ток в реактивных элементах больше тока на входе.

Предположим, что в цепи (Рис. 23.1) действующее значение входного напряжения, индуктивность, емкость и активная проводимость остаются постоянными, а частота входного напряжения изменяется в пределах от нуля до бесконечности. Рассмотрим, как будут изменяться действующие значения токов в ветвях с индуктивностью и емкостью, входного тока, а также угол между напряжением и током на входе.

Действующее значение входного тока как функция частоты:

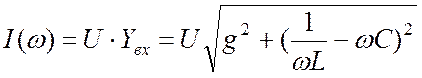                                                 .                                                                               (23.10)

Действующее значение тока в индуктивности как функция частоты:

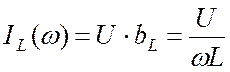                                                                 .        (23.11)

Действующее значение тока в емкости как функция частоты:

                                                               .      (23.12)

Угол между входным напряжением и током как функция частоты:

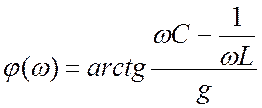                                                               .      (23.13)

Графики функций (23.10-23.13) представлены на Рис. 23.3.

Очень часто встречаются конструкции, в которых нельзя пренебречь активным сопротивлением катушки, а сопротивление резистора, включенного параллельно входу, можно считать бесконечно большим. Тогда схема колебательного контура будет такой, как показано на Рис. 23.4. Рассмотрим некоторые особенности резонанса токов в подобном колебательном контуре.

Основное условие резонанса токов остается прежним:

,

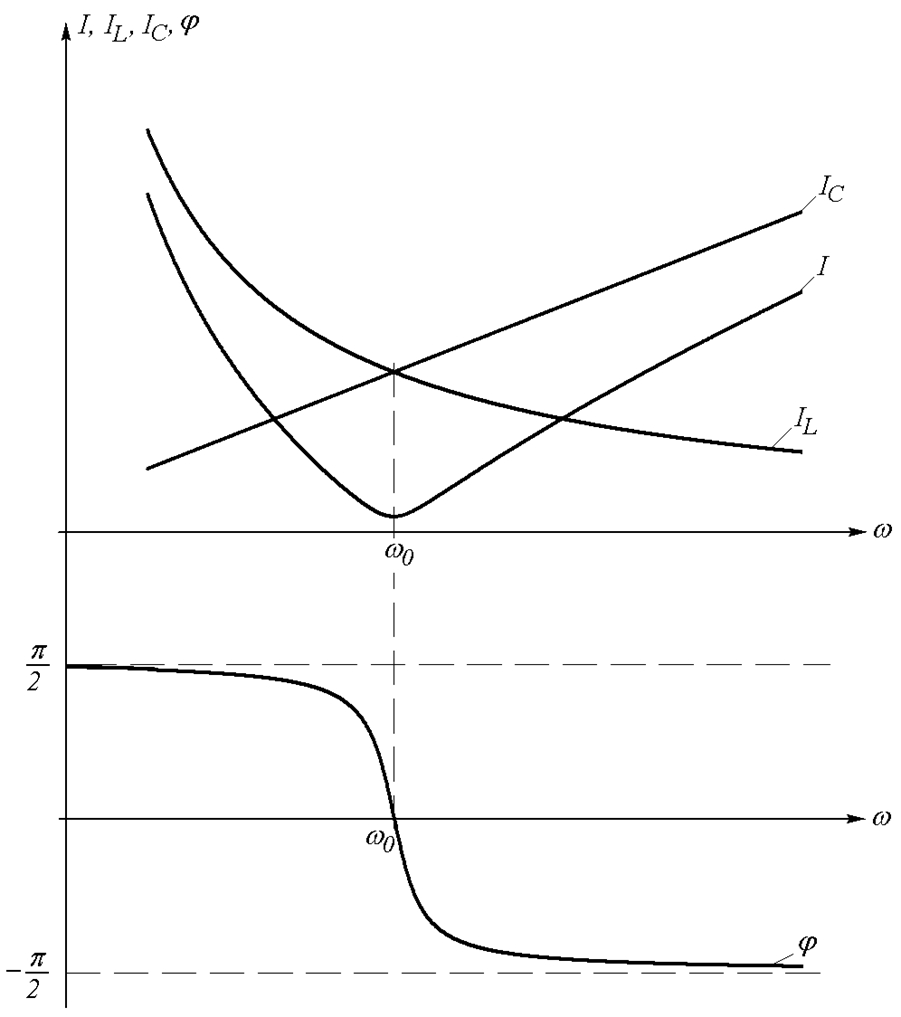
Рис. 23.3

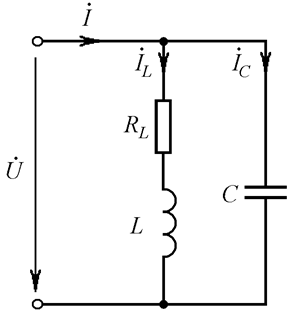
Рис. 23.4

но комплексная входная проводимость теперь определяется выражением:

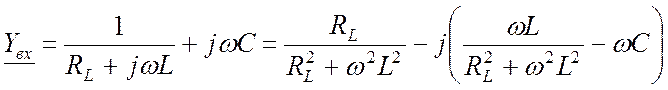            .                                                                               (23.14)

Приравняв к нулю мнимую часть (23.14), получим:

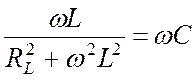                                                                    ,           (23.15)

где 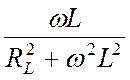      – эквивалентная реактивная проводимость ветви с катушкой.

Резонансную частоту найдем из (23.15):

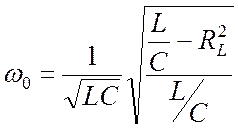                                                                 .        (23.16)

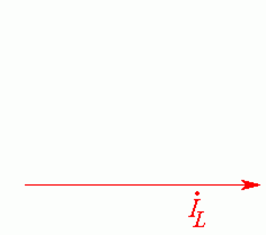
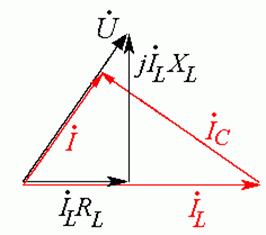
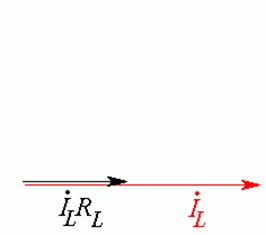
Построим векторную диаграмму. Пусть действующие значения токов и напряжений нам известны (например, получены путем измерений). Диаграмму удобно строить, начиная с ветви с катушкой. Строим вектор тока горизонтально слева направо (Рис. 23.5 а).

Рис. 23.5

Напряжение на активном сопротивлении  совпадает по фазе с током. Строим вектор  параллельно вектору  (Рис. 23.5 б).

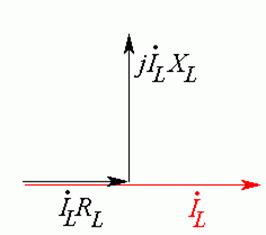
Напряжение на индуктивности  опережает ток на угол . Строим вектор  вертикально вверх из конца вектора  (Рис. 23.5 в).

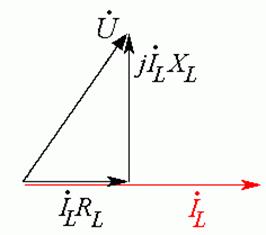
Сумма напряжений на активном сопротивлении и индуктивности равна напряжению на входе. Соединяем начало вектора  с концом вектора  и получаем вектор  (Рис. 23.5 г).

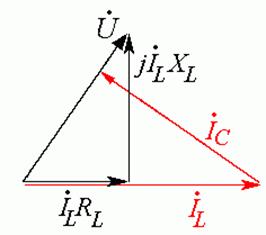
Входное напряжение  приложено и к емкости . Ток на емкости опережает напряжение на угол . При этом, токи  и  в сумме должны дать входной ток . Значит, под прямым углом к вектору  справа налево и вверх, из конца вектора  строим вектор  (Рис. 23.5 д).

Наконец, соединяя начало вектора  с концом вектора , получаем вектор входного тока  (Рис. 23.5 е).

В правильно построенной векторной диаграмме при резонансе токов входной ток должен совпадать по фазе с входным напряжением.

В сложных цепях, содержащих большое количество активных сопротивлений, последовательных и параллельных колебательных контуров (см. например, Рис. 23.6), могут существовать как резонансы напряжений, так и резонансы токов. Резонансы рассчитывают, решая уравнения:

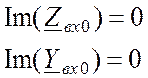                                                                        .               (23.17)

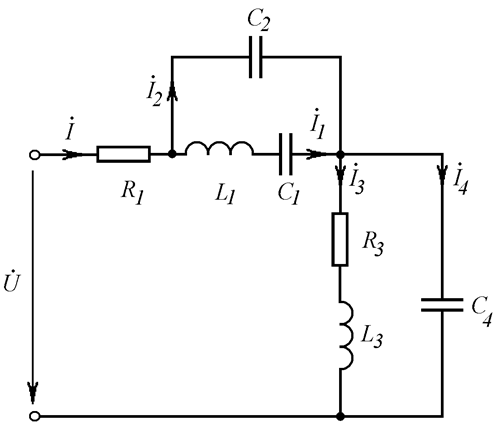
Рис. 23.6

24. ЦЕПИ С МАГНИТНОЙ СВЯЗЬЮ

Магнитная связь – это явление наведения ЭДС в каком-либо контуре цепи при изменении тока в другом контуре этой или другой цепи. Наведенную ЭДС называют ЭДС взаимоиндукции.

Рассмотрим две индуктивные катушки, расположенные на небольшом расстоянии друг от друга. В катушке 1 количество витков равно W₁, в катушке 2 количество витков равно W₂ (Рис. 24.1).

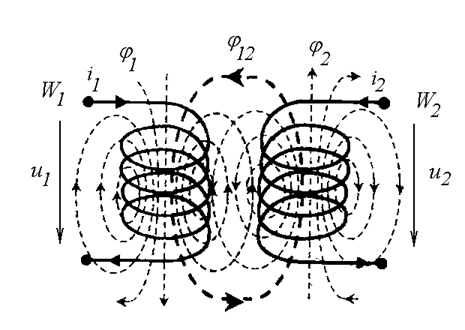
Рис. 24.1