Далі здійснюється перехід до стандартних позначень функції буквою у і аргументу – буквою х. Цей перехід треба пояснити учням.
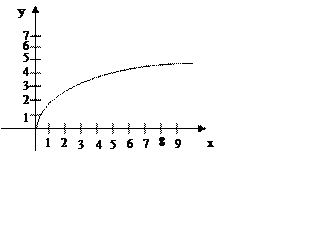 Отже, маємо,
Отже, маємо, ![]() , де
, де ![]() і
і
![]() . Переходячи до побудови графіка
функції
. Переходячи до побудови графіка
функції ![]() , треба пригадати з учнями означення
арифметичного кореня з числа х. Це невід’ємне число, квадрат якого дорівнює х.
Отже, формулою
, треба пригадати з учнями означення
арифметичного кореня з числа х. Це невід’ємне число, квадрат якого дорівнює х.
Отже, формулою ![]() задається функція.
Визначена при всіх невід’ємних значеннях змінної х. Визначається розміщення графіка
функції
задається функція.
Визначена при всіх невід’ємних значеннях змінної х. Визначається розміщення графіка
функції ![]() на координатній площині.
на координатній площині.
Для складання таблиці значень
аргументу і функції можна використати калькулятор. Побудувавши за цими даними
графік (мал..), порівняємо його з графіком функції ![]() ,
де
,
де ![]() . В обох випадках цими графіками є
частина параболи. Графік
. В обох випадках цими графіками є
частина параболи. Графік ![]() розміщений
відносно осі х так само, як графік функції
розміщений
відносно осі х так само, як графік функції ![]() при
при
![]() відносно осі у.
відносно осі у.
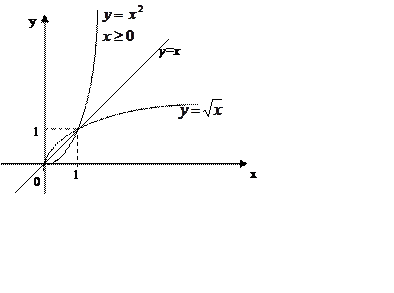 Зобразивши обидва
графіки на одному малюнку, наочно показуємо учням, що вони симетричні відносно
прямої у=х (бісектриси першого координатного кута ).
Зобразивши обидва
графіки на одному малюнку, наочно показуємо учням, що вони симетричні відносно
прямої у=х (бісектриси першого координатного кута ).
За допомогою графіка учні переконуються також, що більшому числу відповідає більше значення квадратного кореня. Переважна більшість вправ за цим матеріалом - на обчислення за допомогою графіка значень аргументу і функції. Але треба приділити достатню увагу і розв’язанню вправ такого змісту:
1. Чи належить графіку ![]() : а) точка А
(-17;5); б) точка В (50; -8)?
: а) точка А
(-17;5); б) точка В (50; -8)?
2. Чи перетинає графік функції ![]() пряма а) у=6;
б) у=-6?
пряма а) у=6;
б) у=-6?
3. Чи існує значення змінної х, при якому: а) ![]() ;
б)
;
б) ![]() ; в)
; в) ![]() ?
?
Відповідаючи на ці запитання, учні
посилаються на умову ![]() і означення арифметичного
кореня.
і означення арифметичного
кореня.
Під час вивчення функції ![]() доцільно повторити поняття “область
значення функції”.
доцільно повторити поняття “область
значення функції”.
Лекція
Тема: Розвиток поняття числа у курсі алгебри основної школи.
План
1 Розширення поняття число.
2 Вивчення раціональних чисел.
3 Дії над натуральними числами.
4 Ірраціональні числа.
5 Дійсні числа.
1. Розширення поняття число.
Різні схеми розвитку поняття числа.
Поняття числа, як
і поняття множини, належать до числа основних фундаментальних понять сучасної
математики. Число є основним знаряддям, за допомогою якого людина пізнає
кількісні відношення реального світу. Поняття натурального числа виникло ще на
початку розвитку людської цивілізації як відображення найпростіших потреб
людської діяльності. Тонує досить природним і те, що сучасне вивчення про число
базується на арифметиці саме натуральних чисел. Зміст подальшого розгортання
цього вчення полягає в тому, що розширення множини натуральних чисел
відбувається за наступною схемою:![]()
![]() , яку називають логічною схемою
розвитку поняття числа.
, яку називають логічною схемою
розвитку поняття числа.
Вивчення чисел у
шкільному курсі математики відбувається у такій послідовності: натуральні
числа, нуль, дробові числа (додатні), від’ємні числа і множина раціональних
чисел, ірраціональні числа і множина дійсних чисел. Ця послідовність відображає
історичний шлях розвитку поняття числа в математиці: ![]() і
має назву історичної схеми розвитку поняття числа. (
і
має назву історичної схеми розвитку поняття числа. (![]() - множина раціональних додатних
чисел).
- множина раціональних додатних
чисел).
Відмінність між історичною і логічною схемами пояснюється тим, що дробові числа історично з’явилися набагато пізніше від’ємних чисел. Адже ще стародавні грецькі математики використовували дробові додатні числа, у той час як багато математиків XVI ст. ще не визнавали від’ємних чисел. Тому за логічною схемою розвитку після натуральних чисел вивчаються цілі числа.
Варто зазначити,
що структура множини Z простіша за структуру
множини ![]() , через те, що перша, як і множина N, є дискретною, а друга –
всюдищільною. Це є однією з переваг логічної схеми.
, через те, що перша, як і множина N, є дискретною, а друга –
всюдищільною. Це є однією з переваг логічної схеми.
Виникає питання: чому є не привести у відповідність схему розвитку поняття числа у шкільному курсі з розвитком цього поняття у сучасній науці? Шкільна схема зазвичай обґрунтовується з точки зору педагогічних міркувань, виходячи з того, що поняття дробового числа (додатнього) простіше (доступніше) для розуміння учнями, ніж поняття від’ємного числа. Взагалі, психолого-педагогічні міркування, що стосуються доступності навчального матеріалу є досить вагомою умовою для відхилення від логіки наукової системи у шкільному навчанні.
Питання щодо схеми розвитку поняття числа і сьогодні залишається на дискусійному рівні.
У шкільному курсі вивчення окремих числових систем має концентричний характер. Тому послідовність вивчення чисел у школі складніша, ніж зазначені вище історична і логічна схеми розвитку поняття числа.
Побудова розширення числової множини повинна задовольняти наступним чотирьом умовам (принципам перманентності і мінімальності).
1) Нова множина чисел повинна містити вже відому множину;
2) Смисл дій над числами в старій множині залишається тим самим у новій множині;
3) У новій множині виконується дія, яку не можна було виконати у старій множині;
4) Нова множина чисел повинна бути такою, щоб не існувало жодної її підмножини, яка містила б попередню множину і задовольняла ті самі умови.
Різні способи побудови.
Нехай множина ![]() - відома множина, яку ми розширюємо
до нової множини
- відома множина, яку ми розширюємо
до нової множини ![]() . Можливі різні способи
побудови множини
. Можливі різні способи
побудови множини ![]() . Множина
. Множина ![]() може бути побудована як нова множина
(незалежно від множини
може бути побудована як нова множина
(незалежно від множини ![]() ), потім у
), потім у ![]() виділяється множина, ізоморфна
множині
виділяється множина, ізоморфна
множині ![]() , яка ототожнюється з множиною
, яка ототожнюється з множиною ![]() . Такий спосіб використання деякий
час у підручнику алгебри А.П.Кисельова і у зв’язку з його надмірною
абстрактністю виявився непридатним для масової школи. З дидактичної точки зору
більш доступним є інший спосіб. Суть його у тому, що для того, щоб отримати
нову роз розширену числову множину
. Такий спосіб використання деякий
час у підручнику алгебри А.П.Кисельова і у зв’язку з його надмірною
абстрактністю виявився непридатним для масової школи. З дидактичної точки зору
більш доступним є інший спосіб. Суть його у тому, що для того, щоб отримати
нову роз розширену числову множину ![]() , яка містить
підмножину, ізоморфну
, яка містить
підмножину, ізоморфну ![]() , ми доповнюємо відому нам
множину
, ми доповнюємо відому нам
множину ![]() новими числами, отримуючи таким чином
нову розширену множину. Саме такий спосіб реалізується у шкільних підручниках.
новими числами, отримуючи таким чином
нову розширену множину. Саме такий спосіб реалізується у шкільних підручниках.
Важливим моментом процесу розширення поняття про число у шкільному навчанні є розкриття ідеї цього розширення, пояснення основної його мети. Не можна обмежуватися у навчанні лише формальним обґрунтуванням необхідності введення нових чисел для забезпечення виконання операцій.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.