Вирази та їх перетворення, страница 2

Поняття про вирази (числові і буквені), тобто вирази зі змінною, формуються описово на конкретних прикладах. Учні повинні вміти розрізняти, розпізнавати числові й буквені вирази. Щодо окремих видів виразів, то вони вводяться поступово, із вивченням програмового матеріалу. Важливі при цьому формулювання усної  алгебраїчної мови, правильна орієнтація у різновидах виразів і їхні назви. Учні повинні усвідомити, що назва виразу визначається не тим виглядом, до якого його можна звести, а тим, який він має при його заданні. 

Поняття тотожно рівних виразів, тотожності вводяться вперше до курсу алгебри 7 класу на рівні означень. У зв’язку з вивченням цілих виразів вводяться означення тотожності як рівності, правильної при будь-яких значеннях змінних. У 8 класі при розгляді дробових виразів після введення поняття допустимих значень змінних наведене означення природно уточнюється: тотожністю називають рівність, правильну при всіх допустимих значеннях змінних, що входять до неї. Далі таке ж розуміння тотожності має місце при вивченні квадратних коренів і степені з раціональним показником.

Аналогічно уточнюється поняття тотожно рівних виразів. Спочатку вони трактуються як вирази, відповідні значення яких рівня при будь-яких значеннях змінних. Далі у зв’язку з введенням поняття допустимих значень змінних тотожно рівними називають вирази, які набувають рівних значень при всіх допустимих для них значеннях змінних. Досвід показує, що поняття тотожно рівних виразів і тотожних перетворень виразів недоцільно розвивати. Природніше ці поняття вводити на одному уроці, пов’язавши з потребою обчислення виразу.

Слід зауважити, що окремі вчителі після розгляду відповідних прикладів намагаються використати проблемну ситуацію і досягти того, щоб учні самостійно  сформулювали означення тотожньо рівних виразів. Але так чинити недоцільно, оскільки за стилем речення і за змістом означення це завдання викликає труднощі в учнів (хоча вони вільно наводять приклади) і призводить лише до марнування навчального часу на уроці.

Поняття одночлена формується конкретно-індуктивним методом, шляхом розгляду прикладів і введення терміна “одночлен”. Важливо, щоб учні усвідомили суттєву ознаку одночленів, за якою вони відрізняються  від інших видів виразів: одночлени є добутком чисел, змінних і степенів змінних. Несуттєвою ознакою одночленів є те, яким буде числовий множник. Він може бути будь-яким числом – цілим, дробовим, додатним, від’ємним, може дорівнювати одиниці. У такому разі одиниця перед буквеним множником не записується. Несуттєвим є і те, скільки змінних і їх степенів входить в одночлен і якими буквами вони позначені. Суттєвим є те, що ця кількість змінних скінчена. Одночленом може бути число. Наприклад, 6;  ;  7,98.

Поняття стандартного вигляду одночлена теж вводяться описово на конкретних прикладах. Поняття многочлена не викликає в учнів труднощів і означається як сума одночленів.

Складнішими для сприйняття  учнями 8 класу є поняття “цілий вираз”, “дробовий вираз” і “дріб”. Пов’язане це в першу чергу з тим, що термін “цілий вираз” в учнів асоціюється з відомим їм поняттям  цілого числа, а “дріб” – з відомим їм поняттям звичайного дробу як числа. Насправді те відому учням поняття дробу є лише формулою запису числа (числового виразу).

У 8 класі доцільно уточнити і розширити уявлення учнів про вирази. Почати слід з поняття раціональних виразів: раціональними називають вирази, які утворені з чисел із змінних за допомогою додавання, віднімання, множення, ділення. Наприклад,

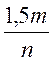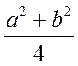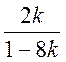;   ;   ;   53;   ;   -3,5;  ;  .

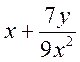Раціональні числа можна розподілити на два класи: цілі числа і дробові числа. Так само і раціональні вирази  можна розподілити на два класи: цілі вирази і дробові вирази.

Цілими називаються вирази, складені з чисел і змінних за допомогою дій додавання, віднімання, множення і ділення на число, відмінне від нуля.

Дробовими раціональними виразами називають раціональні вирази, які містять дію ділення на змінну  або на вираз зі з0мінною.

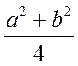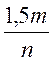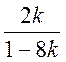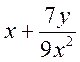Згідно з цими означеннями з наведених вище раціональних виразів вирази ;   ;   53;   -3,5;   - цілі вирази, а вирази  ;  ;    - дробові вирази.

Серед раціональних виразів виділяють  раціональні дроби. Раціональним дробом називають вираз  , де a і b – одночлени або многочлени. Серед наведених вище виразів раціональними дробами є вирази  ;   ;  ;    .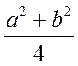

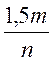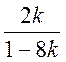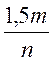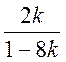Треба домогтися, щоб учні розрізняли поняття “дріб” і “дробовий вираз”. Дробом називається вираз вигляду  , де a і b  - будь-які числові вирази, або вирази зі змінними. Не будь-який дріб є дробовим виразом. Наприклад, вирази  і    - раціональні дроби і дробові вирази, вираз 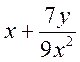 - дробовий вираз, але не раціональний дріб. Будь-який дробовий раціональний вираз можна перетворити і звести до вигляду раціонального дробу.

Лекція

Тема :Алгебра як навчальний предмет у 7 – 9 класах.

План

1. Алгебра як наука і як навчальний предмет.

2. Зміст навчання алгебри основної школи.

1. Алгебра як наука і як навчальний предмет.

Історично алгебра як наука розвивалась з потреб розв'язування рівнянь. Задачі на розв'язування і дослідження рівнянь [вплинули на розвиток поняття числа. Після введення до науки від'ємних, ірраціональних, комплексних чисел загальне дослідження цих числових систем теж стало проблемою алгебри. Введена в алгебру буквена символіка дала змогу записувати властивості дій над числами в стислій формі, зручній для побудови (операцій над буквеними виразами. Загальні дослідження, що [проводились у зв'язку із задачами на розв'язування рівнянь, привели до більш широкого застосування теорій, які відігравали І спочатку лише допоміжну роль під час розв'язування рівнянь як у самій математиці, так і за її межами. Саме ці теорії, до яких належать теорія груп, теорія кілець, теорія полів, лінійна алгебра, теорія Галуа, теорія алгебраїчних чисел, і становлять основний зміст сучасної алгебри.