Вирази та їх перетворення, страница 35

Тотожні перетворення ірраціональних виразів вивчаються в школі відповідно до діючої програми у 2 етапи: у 8 класі учні ознайомлюються з квадратними коренями, їх властивостями і перетвореннями виразів, що містять квадратні корені, у 9 класі дістають відповідні знання і вміння стосовно кореня n–того  степеня з дробовим показником. Перетворення виразів, що містять корені, знаходять широке застосування при вивченні математики в середній школі: під час розв’язування геометричних задач, при розгляді питань, пов’язаних з дослідженнями функцій, при ознайомленні з похідною та її застосуваннями. Крім перетворення добутків, степенів радикалів і спрощення їх найбільш поширеними  перетвореннями, які при цьому доводиться виконувати, є такі:

а)  звільнення від знака кореня знаменника дробу;

б) звільнення від знака кореня чисельника;

в) розкладання на множники виразів, що містять корені, і пов’язані з ними спрощення (скорочення дробів тощо).

Звідси очевидно, наскільки ґрунтовними мають бути знання, що повинні дістати учні і досконалими вміння, якими вони повинні оволодіти, в результаті вивчення цього матеріалу.

Робота по вивченню перетворень виразів, які містять радикали, починається природно із встановлення, що являє собою  , де  - будь-яке дійсне,  - будь-яке натуральне, більше 1. одного означення, що зводиться до формули 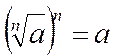 , тут мало: потрібне розуміння того, у яких випадках існує єдине дійсне число, що виражає цей корінь, коли воно не існує, коли існує, але не єдине. Двозначність кореня парного степеня з додатного числа становить велику незручність і її уникають, вводячи поняття арифметичного кореня, тобто невід’ємного його значення.

У курсі алгебри 8 класу перетворення виразів, що містять квадратні корені, передбачають використання означення арифметичного кореня, тотожностей , . Тому належну увагу треба приділити засвоєнню суттєвих ознак квадратного кореня, що уходить в означення. Найбільше помилок учні роблять, виносячи з-під знака кореня числові і буквені множники і вносячи їх під цей знак. Для усунення формалізму в засвоєнні навичок  і умінь виконання тотожних перетворень різних виразів треба поряд із введенням основного завдання перетворення (зведення до стандартного вигляду) домогтись усвідомлення учнями того, що у кожному конкретному випадку метою тотожного перетворення є подання  виразу у вигляді зручному для розв’язування поставленої задачі.

Наведемо приклади:

5.  Обчислюючи значення виразу , коли , , недоцільно розкладати його на множники способом винесення спільного множника за дужки, оскільки за даних значень змінних воно легко обчислюється безпосередньо підстановкою значень змінних.

6.  Якщо треба побудувати графік функції 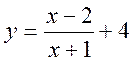 шляхом геометричних перетворень відомого графіка оберненої пропорційності, недоцільно дробовий вираз, що задає функцію, зводити до вигляду дробу. Навпаки, дріб 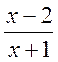 доцільно записати у вигляді суми дробів і перетворити праву частину формули так:

.

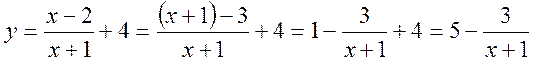Не треба обмежуватись тільки найпростішими перетвореннями. Учитель повинен домогтися, щоб усі восьмикласники могли спрощувати врази, подібні до таких:

 ,    ,    ,   .

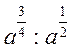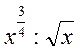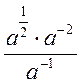Такими повинні бути обов’язкові результати навчання. А ті старшокласники, які готуються складати вступні іспити з математики у вузах, повинні вміти спрощувати, наприклад, і такі вирази:

.

Лекція

Тема: Декартові координати і вектори на площині

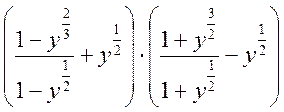План.

1.Загальні поняття.

2.Вектори на площині.

3.Методика введення основних понять.

4.Векторний метод розв’язування задач.

Метод координат - це спосіб визначення положення точки, фігури або інших символів. Числа, за допомогою яких визначається положення точки, називають її координатами.

Прямокутні координати вживались в геометрії з давніх-давен. Зокрема, Аполлоній Пергський (бл. 262 - бл. 190 до н. е.) за допомогою них визначав і досліджував, щоправда, в геометричній термінології, еліпс, параболу, гіперболу. Вперше ідеї методу координат систематично виклали за допомогою невід'ємних чисел П. Ферма (1601 - 1655) і Р. Декарт. І. Ньютон ввів від'ємні координати, а Г. Лейбніц - термін «координати».                                             

Перевага методу координат перед синтетичним методом, за якого безпосередньо розглядаються фігури і кожна задача потребує особливого підходу, в його алгоритмічності. Справді, за допомогою методу координат будь-яка геометрична задача зводиться до алгебраїчної, а алгебраїчні задачі легше алгоритмізуються.

У наш час багато хто із фахівців використовує знання і вміння, здобуті при вивченні методу координат у школі. Лікар будує графік температури хворого, економіст - графік зміни випуску продукції на виробництві, фізик за допомогою графіків у певній системі координат досліджує фізичні явища і т. ін. У математиці широко послуговуються не тільки прямокутною декартовою системою координат, а й іншими системами: сферичними, циліндричними, еліптичними та ін. Метод координат є основним методом дослідження властивостей геометричних фігур в аналітичній геометрії.

Із введенням методу координат до шкільного курсу геометрії розширюється набір аналітичних методів. До таких методів крім методу рівнянь в алгебрі належать векторний метод і метод, що спирається на використання тригонометричних функцій. Координатний метод спрощує розв'язання багатьох геометричних задач, доведення теорем, дає можливість спростити виклад теоретичного матеріалу, що стосується векторів, тригонометричних функцій. Метод координат дає змогу встановити тісні зв'язки з алгеброю, фізикою, географією, астрономією, застосовувати сучасні ЕОМ не тільки до розв'язування обчислювальних задач, а н до розв'язування геометричних задач, дослідження геометричних об'єктів, співвідношень, графічних завдань.

Відповідно до чинної програми вперше поняття «координата точки на прямій», «прямокутна система координат на площині» вводяться в курсі математики 6 класу. У курсі алгебри 7-9 класів здобуті знання і вміння застосовуються при побудові графіків функцій, графічному розв'язуванні рівнянь, нерівності та їх систем. У курсі геометрії 8 класу знову передбачені вивчення декартових координат і застосування методу координат до досліджений властивостей геометричних фігур і означення тригонометричних функцій кута від 0° до 180°, вивчення функцій.