а) звільнення від знака кореня знаменника дробу;
б) звільнення від знака кореня чисельника;
в) розкладання на множники виразів, що містять корені, і пов’язані з ними спрощення (скорочення дробів тощо).
Звідси очевидно, наскільки ґрунтовними мають бути знання, що повинні дістати учні і досконалими вміння, якими вони повинні оволодіти, в результаті вивчення цього матеріалу.
Робота
по вивченню перетворень виразів, які містять радикали, починається природно із
встановлення, що являє собою ![]() , де
, де ![]() - будь-яке дійсне,
- будь-яке дійсне, ![]() - будь-яке
натуральне, більше 1. одного означення, що зводиться до формули
- будь-яке
натуральне, більше 1. одного означення, що зводиться до формули 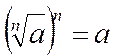 , тут мало:
потрібне розуміння того, у яких випадках існує єдине дійсне число, що виражає
цей корінь, коли воно не існує, коли існує, але не єдине. Двозначність кореня
парного степеня з додатного числа становить велику незручність і її уникають,
вводячи поняття арифметичного кореня, тобто невід’ємного його значення.
, тут мало:
потрібне розуміння того, у яких випадках існує єдине дійсне число, що виражає
цей корінь, коли воно не існує, коли існує, але не єдине. Двозначність кореня
парного степеня з додатного числа становить велику незручність і її уникають,
вводячи поняття арифметичного кореня, тобто невід’ємного його значення.
У
курсі алгебри 8 класу перетворення виразів, що містять квадратні корені,
передбачають використання означення арифметичного кореня, тотожностей ![]() ,
, ![]() . Тому належну
увагу треба приділити засвоєнню суттєвих ознак квадратного кореня, що уходить в
означення. Найбільше помилок учні роблять, виносячи з-під знака кореня числові
і буквені множники і вносячи їх під цей знак. Для усунення формалізму в
засвоєнні навичок і умінь виконання тотожних перетворень різних виразів треба
поряд із введенням основного завдання перетворення (зведення до стандартного
вигляду) домогтись усвідомлення учнями того, що у кожному конкретному випадку
метою тотожного перетворення є подання виразу у вигляді зручному для
розв’язування поставленої задачі.
. Тому належну
увагу треба приділити засвоєнню суттєвих ознак квадратного кореня, що уходить в
означення. Найбільше помилок учні роблять, виносячи з-під знака кореня числові
і буквені множники і вносячи їх під цей знак. Для усунення формалізму в
засвоєнні навичок і умінь виконання тотожних перетворень різних виразів треба
поряд із введенням основного завдання перетворення (зведення до стандартного
вигляду) домогтись усвідомлення учнями того, що у кожному конкретному випадку
метою тотожного перетворення є подання виразу у вигляді зручному для
розв’язування поставленої задачі.
Наведемо приклади:
3.
Обчислюючи значення виразу ![]() , коли
, коли ![]() ,
, ![]() , недоцільно розкладати його на
множники способом винесення спільного множника за дужки, оскільки за даних
значень змінних воно легко обчислюється безпосередньо підстановкою значень
змінних.
, недоцільно розкладати його на
множники способом винесення спільного множника за дужки, оскільки за даних
значень змінних воно легко обчислюється безпосередньо підстановкою значень
змінних.
4.
Якщо треба побудувати графік функції 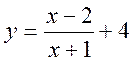 шляхом геометричних перетворень
відомого графіка оберненої пропорційності, недоцільно дробовий вираз, що задає
функцію, зводити до вигляду дробу. Навпаки, дріб
шляхом геометричних перетворень
відомого графіка оберненої пропорційності, недоцільно дробовий вираз, що задає
функцію, зводити до вигляду дробу. Навпаки, дріб 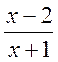 доцільно записати у вигляді суми
дробів і перетворити праву частину формули так:
доцільно записати у вигляді суми
дробів і перетворити праву частину формули так:
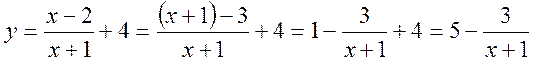 .
.
Не треба обмежуватись тільки найпростішими перетвореннями. Учитель повинен домогтися, щоб усі восьмикласники могли спрощувати врази, подібні до таких:
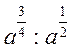 ,
, 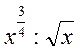 ,
, ![]() ,
, 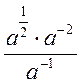 .
.
Такими повинні бути обов’язкові результати навчання. А ті старшокласники, які готуються складати вступні іспити з математики у вузах, повинні вміти спрощувати, наприклад, і такі вирази:
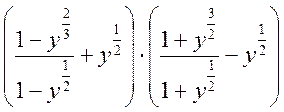 .
.
Лекція
Тема: Розвиток поняття числа у курсі алгебри основної школи.
План
1 Розширення поняття число.
2 Вивчення раціональних чисел.
3 Дії над натуральними числами.
4 Ірраціональні числа.
5 Дійсні числа.
3. Розширення поняття число.
Різні схеми розвитку поняття числа.
Поняття числа, як
і поняття множини, належать до числа основних фундаментальних понять сучасної
математики. Число є основним знаряддям, за допомогою якого людина пізнає
кількісні відношення реального світу. Поняття натурального числа виникло ще на
початку розвитку людської цивілізації як відображення найпростіших потреб
людської діяльності. Тонує досить природним і те, що сучасне вивчення про число
базується на арифметиці саме натуральних чисел. Зміст подальшого розгортання
цього вчення полягає в тому, що розширення множини натуральних чисел
відбувається за наступною схемою:![]()
![]() , яку називають логічною схемою розвитку поняття числа.
, яку називають логічною схемою розвитку поняття числа.
Вивчення чисел у
шкільному курсі математики відбувається у такій послідовності: натуральні
числа, нуль, дробові числа (додатні), від’ємні числа і множина раціональних
чисел, ірраціональні числа і множина дійсних чисел. Ця послідовність відображає
історичний шлях розвитку поняття числа в математиці: ![]() і має назву історичної схеми розвитку поняття числа. (
і має назву історичної схеми розвитку поняття числа. (![]() - множина раціональних додатних чисел).
- множина раціональних додатних чисел).
Відмінність між історичною і логічною схемами пояснюється тим, що дробові числа історично з’явилися набагато пізніше від’ємних чисел. Адже ще стародавні грецькі математики використовували дробові додатні числа, у той час як багато математиків XVI ст. ще не визнавали від’ємних чисел. Тому за логічною схемою розвитку після натуральних чисел вивчаються цілі числа.
Варто зазначити,
що структура множини Z простіша за структуру
множини ![]() , через те, що перша, як і множина N, є дискретною, а друга –
всюдищільною. Це є однією з переваг логічної схеми.
, через те, що перша, як і множина N, є дискретною, а друга –
всюдищільною. Це є однією з переваг логічної схеми.
Виникає питання: чому є не привести у відповідність схему розвитку поняття числа у шкільному курсі з розвитком цього поняття у сучасній науці? Шкільна схема зазвичай обґрунтовується з точки зору педагогічних міркувань, виходячи з того, що поняття дробового числа (додатнього) простіше (доступніше) для розуміння учнями, ніж поняття від’ємного числа. Взагалі, психолого-педагогічні міркування, що стосуються доступності навчального матеріалу є досить вагомою умовою для відхилення від логіки наукової системи у шкільному навчанні.
Питання щодо схеми розвитку поняття числа і сьогодні залишається на дискусійному рівні.
У шкільному курсі вивчення окремих числових систем має концентричний характер. Тому послідовність вивчення чисел у школі складніша, ніж зазначені вище історична і логічна схеми розвитку поняття числа.
Побудова розширення числової множини повинна задовольняти наступним чотирьом умовам (принципам перманентності і мінімальності).
9) Нова множина чисел повинна містити вже відому множину;
10) Смисл дій над числами в старій множині залишається тим самим у новій множині;
11) У новій множині виконується дія, яку не можна було виконати у старій множині;
12) Нова множина чисел повинна бути такою, щоб не існувало жодної її підмножини, яка містила б попередню множину і задовольняла ті самі умови.
Різні способи побудови.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.