Вирази та їх перетворення, страница 4

мати уявлення про початкові поняття статистики і теорії ймовірностей, про способи перерахунку елементів скінченних множин, розуміти смисл перестановок, розміщень і сполук;

розуміти поняття «ймовірність», «частота», вміти підраховувати ймовірності в найпростіших випадках і розв'язувати простіші задачі за допомогою формул комбінаторики.

Лекція

Тема:Вчення про функцію в шкільному курсі алгебри основної школи.

План

1.  Місце теми в програмі

2.  Вимоги до знань і умінь

3. Розвиток поняття функції.

4. Різні означення функції.

5. Функціональна пропедевтика.

1.Місце теми в програмі.

Поняття функції – одне з фундаментальних математичних понять – пронизує весь курс алгебри. За чинною програмою поняття функції і відповідне означення явно вводяться у 7 класі. Зважаючи на те, що програма курсу алгебри 7-го класу перевантажена навчальним матеріалом, який закладає основи цього навчального предмета, проект нової програми передбачає вводити поняття функції і вивчати функці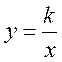ї: ,  ,  ,   ,      і   у 8-му класі, а функцію ,     - у 9-му класі.

Але сьогодні функції у шкільному курсі алгебри вивчаються наступним чином. У 7-му класі вводиться поняття про функцію, розглядається лінійна функція та її графік. Ці відомості використовуються для геометричної інтерпретації системи двох лінійних рівнянь з двома змінними і їх розв’язку. У цьому ж класі у розділі “степінь з натуральним показником” розглядаються функції ,   , що дає змогу продовжити роботу з формування умінь будувати і читати графіки. У 8-му класі у зв’язку з вивченням квадратних коренів учні знайомляться з функцією  , її властивостями і графіком, встановлюють взаємозв’язок між  функціями  і   ().

Розглядаються також функці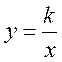ї   і .

Квадратична функція  розглядається у 9-му класі.   Вивчення її властивостей пов’язується з розв’язуванням нерівностей другого степеня з однією змінною, а також нескладних раціональних нерівностей методів інтервалів.

Певне узагальнення весь матеріал про функцію дістає у 9-му класі в розділі “Степінь з раціональним показником”, де вводиться поняття степеневої функції .

Таким чином, функціональна лінія пронизує весь курс алгебри 7-9 класів і розвивається у тісному взаємозв’язку з тотожними перетвореннями, рівняннями і нерівностями.

2.Вимоги до знань і умінь.

Основна мета вивчення функцій у шкільному курсі алгебри – сформувати уявлення про функції як математичні моделі залежності між величинами й об’єктами, будь-якої природи, на прикладах прямої й оберненої пропорційності ввести поняття про основні способи задання функцій, розглянути функції ,  ,  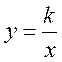,   ,     , ,     та їх графіки, табличні способи задання. Властивості функцій встановлюються за їх графіками, тобто на основі наочних уявлень, і лише деякі властивості обґрунтовуються аналітично. В міру оволодіння учнями теоретичним матеріалом кількість властивостей, що підлягають вивченню, поступово збільшується.

Програмою задано такий обов’язковий мінімум умінь, пов’язаний з вивченням функції:

-  розуміти зміст поняття “функція”, знати три основні способи задання функцій;

-  розуміти суттєві ознаки функцій, передбачених програмою, розпізнавати їх серед інших функцій, що задані формулою, вміти будувати їх графіки, читати за графіками властивості, наводити приклади залежностей, які виражаються ними.

3.  Розвиток поняття функції.

Поняття функції, як і поняття числа пройшло довгий історичний шлях уточнення і розширення. Воно виникло х потреб практики й таких наук, як фізика, хімія, природознавство та ін. Поняття “функція” було введено в математику в кінці XVII століття. Вперше Р.Декарт досліджував, як змінюється ордината точки залежно від зміни її абсциси, але терміна “функція” він не вживав. Вперше термін “функція” використав у своїх працях Г.Лейбніц, пов’язуючи його з геометричними уявленнями. Він також ввів терміни “змінна”, “константа”. Перше означення функції сформулював учень і співпрацівник Лейбніца Й.Бернуллі в 1718 році: функцією змінної величини називають кількість, яка утворена будь-яким способом  з цієї змінної величини і сталих.

У 1748 році це означення було уточнене Л.Ейлером: функція змінної кількості – це аналітичний вираз, складений якимсь чином з цієї кількості і чисел або сталих кількостей.

Отже, перше означення функцій Й.Бернуллі і Л.Ейлер пов’язували з аналітичним виразом, що її задає. Однак таке тлумачення звужувало поняття функція і гальмувало дальший розвиток математичної науки та її застосувань.

Минуло понад 100 років після введення першого означення функцій Й.Бернуллі, поки М.І.Лобачевський 1834 р. не сформулював більш загальне означення функції: число, яке задається для кожного х і разом з х поступово змінюється; значення функції можна задати або аналітичним виразом, або умовою, яка подає засіб випробовувати всі числа і вибирати одне з них; нарешті, залежність може існувати і залишатися невідомою.

Три роки по тому П.Діріхле дійшов висновку, що спосіб встановлення відповідності між значеннями х і у неважливий, і дав таке означення функції: у є функцією від х, якщо будь-якому значенню х відповідає цілком певне значення у, причому зовсім несуттєво, яким саме способом встановлено зазначену відповідність [1].

Отже в основу означень М.І.Лобачевского і П.Діріхле явно покладена ідея відповідності.

У XX столітті поняття функції розширювалося далі. П.Дірак у 1930 році ввів нове поняття “дельта-функція”. За допомогою якого описував явища квантової механіки. С.Л.Соболєв ввів поняття “узагальнена функція”, яке включає як окремий випадок поняття “дельта-функція” для розв’язування задач математичної фізики.

Доречним є вислів Г.Шилова про те, що під впливом нових вимог математики та інших наук означення функції буде і надалі змінюватися, і кожна наступна зміна, як і попередня, відкриватиме нові горизонти науки і приводитиму до нових важливих відкриттів.

4.  Різні означення функції.

Аналіз навчально0-методичної літератури для шкіл і вищих навчальних закладів свідчить про те, що в ній поширені два напрями у тлумаченні поняття функції: класичний і сучасний.