У паралельних підручниках геометрії по-різному визначене місце методу координат. У підручнику О. В. Погорєлова «Декартові координати на площині» пропонується у 8 класі • широко використовується для вивчення властивостей геометричних фігур векторів, паралельного перенесення. У підручнику С. Атанасяна та ін «Метод координат» передбачено вивчати в 9 класі після вивчення векторів і застосовувати його до розкладання векторів по двох неколінеарних векторах, обчисленим скалярного добутку векторів, розв'язування найпростіших задач в координатах і виведення рівняння кола та прямої.
Основна мета вивчення декартових координат в школі - сформувати поняття про координати точки на прямій і площині, вміння знаходити точку за її координатами і розв'язувати обернену задачу, знаходити відстань між двома точками і координати середини відрізка, застосовувати метод координат при розв'язуванні простіших задач і дальшому вивченні курсу математики та суміжних предметів.
Вивчення декартових координат у 5-6 класах. Підготовча робота до введення координатної площини починається вже в 5 класі, де вводиться поняття «числовий промінь» і показується, як зображуються на ньому натуральні числа.
У 6 класі для зображення додатних і від'ємних чисел вводиться числова вісь. Учні повинні усвідомити, що положення точки А на прямій цілком визначається одним числом, яке називається координатою точки і позначається А (3), В (7,8), М(х). Варто звернути увагу учнів на те, що одним числом визначають положення точки не лише на прямій. Наприклад, положення супутника на траєкторії, по якій він рухається навколо Землі, визначається числом, що дорівнює відстані, яку він подолав від певної точки траєкторії; положення рухомого транспорту на залізниці чи автостраді можна визначити за номером кілометрового стовпа, який допоможе визначити відстань від певного пункту.
Після введення поняття координатної площини (на прикладі залу кінотеатру) корисно навести інші приклади застосування системи координат. Наприклад: географічна карта (за допомогою широти і довготи визначається положення будь-якого населеного пункту), шахова дошка (положення фігури визначається за допомогою двох символів - малої літери латинського алфавіту і цифри). Використання двох символів для позначення положення шахової фігури на дошці (наприклад, король а2) дає можливість транслювати хід шахових змагань з будь-якого міста земної кулі.
У 6 класі поняття про координати точки на прямій і на площині вводяться описово на прикладах. Тут ще не ставиться за мету вводити означення абсциси і ординати. Важливо, щоб учні усвідомили, що координата точки на прямій - це число, модуль якого дорівнює відстані точки прямої від початку відліку - точки О. Модулі першої і другої координат точки Μ на координатніq площині задають відстані цієї точки від осі х і осі у. Вся система вправ на цьому етапі має бути спрямована на формування уміння розв'язувати пряму і обернену задачі на визначення положення точки на координатній прямій і площині.
Висловимо зауваження щодо термінології і символіки, пов'язаних з методом координат. На жаль, у шкільних підручниках немає щодо цього єдності. В одному вводиться термін «числова вісь» та його синоніми «числова пряма», «координатна вісь». В іншому використовується термін «координатна пряма» в тому ж самому розумінні. У посібнику з алгебри і початків аналізу вживаються два терміни: «числова пряма» і «координатна пряма», причому в них вкладається різний зміст. Координатна пряма - це пряма, на якій обрано початок відліку, напрямок і одиницю відліку. Числова пряма - це множина R всіх дійсних чисел. Числова пряма - одна, а координатних прямих - багато. У підручнику геометрії Погорєлова вживається термін «осі координат». По-різному позначаються осі координат. У підручнику геометрії Погорєлова, підручниках математики 5-6 класів вживаються позначення «вісь х», «вісь у», а в підручнику алгебри і початків аналізу Колмогорова, підручнику геометрії Атанасяна - «вісь Ох», «вісь Оу».
Наголошуємо, що, починаючи з 6 класу, треба в усіх шкільних предметах дотримуватися однакової термінології і символіки.
Метод координат в курсі геометрії. Вивчення у 8 класі теми «Координати на площині» треба починати з повторення і зведення в систему тих знань і умінь, які учні вже мають з попередніх класів. Це можна зробити за такою системою запитань і завдань.
1. Що таке вісь координат?
2. Чим визначається положення точки на осі координат?
3. Як називається число, за допомогою якого визначається положення точки на осі координат?
4. Як записати точку, задану своєю координатою на прямій? Як знайти її положення на осі координат?
5.
Позначити на осі координат точки ![]()
6. Записати точки, позначені на осі координат, через їх координати.
7. Що таке координатна площина?
8. Чим визначається положення точки на координатній площині?
9. Як називаються координати точки на координатній площині?
10. Як символічно записується точка, задана своїми координатами на площині?
11. Позначити на
координатній площині точки ![]()
![]()
12. Записати точки за їх координатами, які позначені на координатній площині.
13. Навести приклади застосування координат.
На відміну від 6 класу в курсі геометрії 8 класу тема «Декартові координати на площині» вивчається на більш високому теоретичному рівні і в ширшому застосуванні. Зокрема, тут вводяться означення абсциси х і ординати у точки А. У підручнику О. В. Погорєлова вони означаються через термін «абсолютна величина числа», якого учні не знають з курсу алгебри. Тому доцільно вжити термін «модуль числа». До того ж можна взяти більш вдалий для сприймання учнів термін «відстань». Зокрема, виконавши рисунок 3.34, можна звернути увагу учнів на те, що АХО = = ААУ, а ААУ - відстань точки А до осі у. Тому означення абсциси формулюють і так: абсцисою точки А називається число ;с, модуль якого дорівнює відстані точки А від осі у.
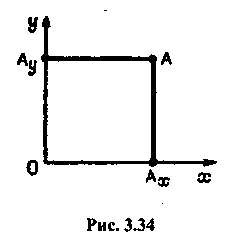
Аналогічно можна сформулювати означення ординати. Вчитель повідомляє учням про те, що термін «декартові» щодо координат пов'язаний з ім'ям Р. Декарта, який уперше ввів їх до математики.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.