Вирази та їх перетворення, страница 22

Загальний висновок: щоб від одного числа відняти друге число, треба до зменшуваного додати число, протилежне від’ємнику. До цього висновку можна прийти інакше, використовуючи означення дії віднімання.

Доцільність прийняття правила знаків при множенні додатних і від’ємних чисел  найкраще пояснити потребами самої математики: ми приймаємо такі правила знаків, щоб закони дій, встановлені для додатних чисел, залишались в силі і для від’ємних чисел. Треба прийняти три твердження щодо добутку двох від’ємних чисел, чисел з різними знаками і умову рівності нулю добутку.

З цих тверджень випливають правила множення, які показують учням, що треба робити при множенні таких чисел: 1) щоб перемножити два відємні числа, треба перемножити модулі і поставити перед результатом знак “+”; 2) щоб перемножити два числа з різними знаками, треба перемножити їх модулі і поставити перед результатом знак “-”.

Далі ці два правила закріплюються шляхом розв’язування вправ, серед яких мають бути натуральні числа, десяткові і звичайні дроби. Для підготовки до розв’язування важливим є твердження, що виражає необхідну і достатню умову рівності нулю добутку двох або кількох співмножників, які є числами або цілими алгебраїчними виразами.

Якщо хоча б один з множників дорівнює нулю, то і добуток дорівнює нулю.

Для конкретного тлумачення смислу множення двох від’ємних чисел, або множення додатнього числа від’ємне використовують вправи, розв’зування яких пов’зане із переміщенням  уздовж координатної прямої.

Під час введення дії ділення додатних і від’ємних чисел доцільно відразу є звернути увагу учнів на те, що вона, як і раніше, тлумачиться, як дія, обернена множенню. Після розв’язування кількох вправ на  основні означення ділення учня самі зможуть сформулювати правило ділення двох від’ємних чисел і ділення чисел з різними знаками.

Важливо показати учням застосування законів дій для раціоналізації обчислень, розв’зування рівнянь, спрощення виразів. Завершити вивчення раціональних чисел варто  уточненням  понять “раціональне число”, “множина раціональних чисел”, звернути увагу на те, що в цій множині виконуються всі чотири арифметичні дії, крім ділення на нуль.

4.Ірраціональні числа.

Відомо, що для практичних обчислень множини раціональних чисел недостатньо. Тому розширення множини раціональних чисел слід мотивувати перш за все внутрішніми математичними потребами . традиційно введення нових, ірраціональних чисел пов’язують із задачею вимірювання відрізків. Але також можна розглянути і наступні задачі:

6.  Чи є значення квадратного кореня з числа 2 раціональним числом?

7.  Які корені рівняння ?

8.  Яким числом виражається довжина діагоналі зі стороною 1?

9.  Чому дорівнює сторона квадрата, якщо його площа дорівнює 3?

10. Чи кожній точці координатної прямої відповідає деяке раціональне число?

У сучасних умовах роботи за чинною програмою треба вивчати раціональні числа і множину дійсних чисел у 8 класі на доступнішому, ніж у традиційному шкільному курсі математики, рівні за коротший час, без багатьох означень і доведень, або фактично на рівні уявлень. Тому мотивування і введення раціональних чисел можна здійснити за таким методичним варіантом.

На одиничному відрізку координатної прямої будується квадрат (мал.  ) і ставиться за мету визначити довжину його діагоналі ОК, а відповідне число зобразити точкою Р на координатній прямій. Геометрично це виконується легко відкладанням  циркулем відрізка ОК

 на координатній прямій.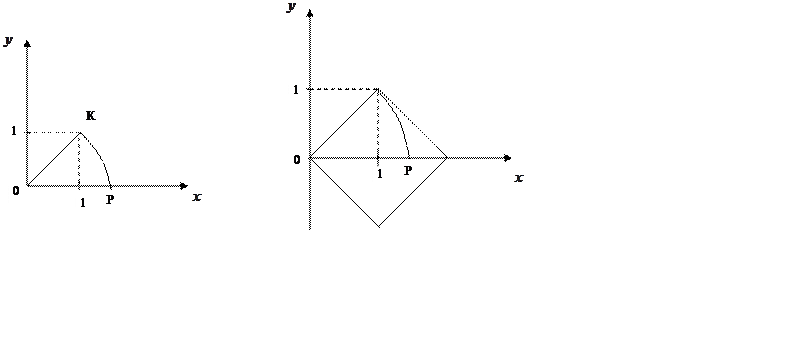

Щоб з’ясувати, яким числом виражається координата  точки К, позначимо довжину відрізка ОК буквою Х і побудуємо ще один квадрат, стороною якого є  відрізок ОК (мал.  ). З рисунка видно, що площа цього квадрата вдвоє більша за площу одиничного квадрата. Отже, , оскільки площа одиничного квадрата дорівнює 1.

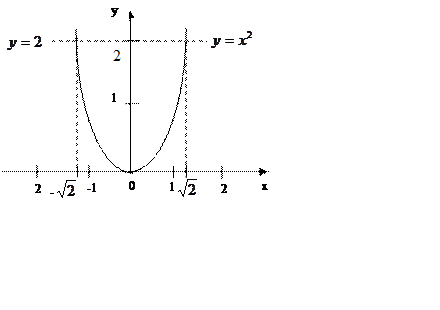
Щоб визначити , треба розв’язати одержане квадратичне рівняння. Графічний спосіб його розв’язування (мал.  ) свідчить про, те існують два корені цього рівняння. Квадрат кожного з них дорівнює 2. з попереднього навчального матеріалу учні вже знають , що число, квадрат якого дорівнює 2, називається квадратним коренем. Арифметичний квадратний корінь позначається символом . Тому два корені рівняння  є не що інше, як числа ; . Які це числа?

Далі формулюється і доводиться методом від супротивного твердження: не існує раціонального числа, квадрат якого дорівнює 2.

Отже, корені рівняння  і  не належать  до раціональних чисел. Звертається увага на те, що не є раціональними також числа: , , ,.... Такі числа називають ірраціональними. Сполучення “ir” латинською мовою означає “не”. Кожне ірраціональне число можна записати у вигляді якогось нескінченного неперіодичного десяткового дробу. І навпаки, кожен нескінчений неперіодичний десятковий дріб позначає якесь ірраціональне число.

5.Дійсні числа.

З приводу вивчення дійсних чисел у шкільному курсі було висловлено різні, навіть суперечливі точки зору. З одного боку, існує версія, що викласти теорію дійсних чисел у школі більш-менш коректно неможливо з огляду на надзвичайні труднощі такого викладення. З іншого – у неточно математичній літературі зустрічаються спроби налаштувати  яку-небудь з відомих побудов теорії дійсних чисел (за Вейерштрассом, за Дедекіндом чи за Кантором) під шкільне навчання. Було висловлено також і протилежні думки щодо необхідності строгої і розвинутої теорії дійсних чисел у шкільному навчанні.

Безсумнівно, що вчителю корисно бути ознайомленим з різними побудовами шкільного вчення про дійсні числа, які в деякій мірі висвітлюють ідеї, що лежать в основі відповідних наукових побудов  теорії дійсних чисел.

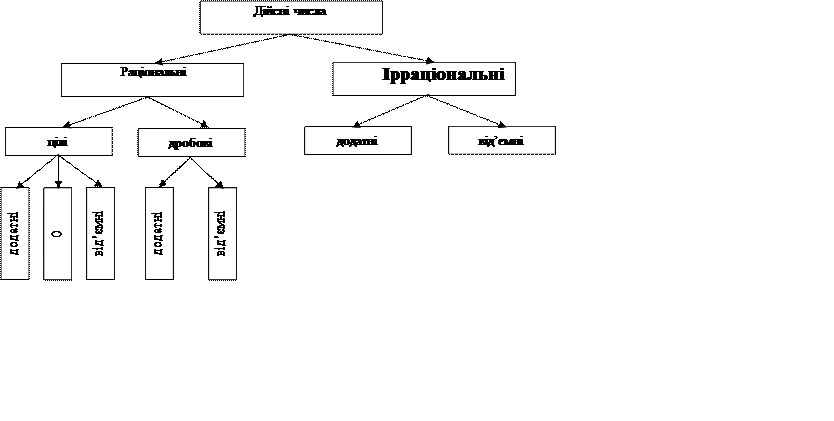
Вводити дійсні числа можна за відомою учням схемою. Числа натуральні, нуль і протилежні натуральним становлять множину цілих чисел. Числа цілі і дробові становлять множину раціональних чисел. Аналогічно: числа раціональні і ірраціональні становлять множину дійсних чисел. Сказане бажано ілюструвати конкретними прикладами і за допомогою схеми: