Вирази та їх перетворення, страница 28

Не треба плутати поняття “множина натуральних чисел” і “натуральний ряд”. Коли говорять про множину натуральних чисел, то порядок чисел вважають неістотним. Натуральний ряд дістають тільки тоді, коли впорядковують цю множину. Але про це можна сказати пізніше, під час вивчення порівняння натуральних чисел.

3.Дії над натуральними числами.

Практика свідчить про те, що дії учнів, які навчилися виконувати чотири дії над натуральними числами в початковій школі, виконання дій над багатоцифровими числами не становить жодних труднощів.

Доцільно провести діагностику знань, навичок і умінь учнів для того, щоб ефективно здійснювати диференційоване навчання, з погляду як складності навчального матеріалу, так і рівня вимог до окремих категорій учнів.

Слід враховувати і те, що основний матеріал про дії над натуральними числами учням відомий. Тому вчителеві важко підтримувати постійний пізнавальний інтерес на уроці і під час виконання домашніх завдань, широко залучати наочність, історичні довідки.

Важливою умовою є дотримання наступності з курсом початкової школи.

Першою завжди розглядають дію виконання. Краще починати з конкретної практичної задачі, розв’язування якої зводиться до визначення суми двох натуральних чисел. Розв’язавши задачу, слід повторити дію додавання і доцільно уточнити такі питання.

15.  Спираючись на запис чисел у вигляді суми розрядних одиниць і закони додавання, теоретично обґрунтовувати правило додавання багатоцифрових чисел, розглянувши конкретні приклади спочатку без переходу через десяток. Достатню увагу треба приділити додаванню, яке вимагає переходу через десяток..

Важливо наголосити учням на застосування законів додавання для раціоналізації обчислень, розглянувши приклади типу

;  .

16.  Спеціального розгляду потребує питання про зміну суми залежно від суми доданків, що елементом пропедевтики вивчення поняття функції у 7 класі.

17.  Повторити додавання натурального числа до нуля і нуля – до натурального числа. Обґрунтувати властивість нуля у разі додавання важко, оскільки учням не вводиться означення дії додавання.

18.  Слід підкреслити можливість і однозначність дії додавання двох натуральних чисел, натурального числа і нуля. Це важливо з погляду ідеї розширення поняття про число.

19.  Доцільно наголосити на тому, які задачі розв’язуються дією додавання. На прикладі двох конкретних задач учні повинні дійти висновку, що дією додавання розв’язуються дві різні за математичним змістом задачі. У першій задачі знаходять суму двох доданків, а в другій – дане число збільшують на декілька одиниць.

20.  З погляду пропедевтики вивчення різних  видів виразів варто звернути увагу учнів на неоднозначність вживання терміна “сума”. Від вживається у двох значеннях: як результат дії додавання і як вираз, що складається з двох або кількох чисел (або букв), сполучених знаком “+”. Аналогічне зауваження стосується і термінів “різниця”, “добуток”, “частка”.

21.  Доцільно зауважити, що перевірка дії додавання виконується за допомогою цієї самої дії перестановкою доданків.

Відніманням часто називають дію, за допомогою якої за даною сумою і одним даним доданком знаходимо другий доданок. Це означає не строге з наукового погляду, а основне – воно не діє. Віднімання в шкільних підручниках означається як дія, обернена додаванню. Найвдаліше це означення подається в такому формулюванні: відняти від числа  число  означає знайти таке число , яке в сумі з числом  дає . Позначається: . Саме таке означення неодноразово доведеться формулювати при відніманні дробів, раціональних і дійсних чисел, а також для многочленів, раціональних та інших виразів. На цьому етапі навчання важливо вдосконалити навички віднімання багатозначних натуральних чисел, звернути особливу увагу на складні випадки віднімання.

Важливо, щоб учні усвідомили можливість двох способів перевірки для віднімання: 1) додаванням, знаходячи зменшуване за від’ємником і різницею; 2) відніманням, знаходячи від’ємник за зменшуваним і різницею.

Обґрунтування рівностей  і  здійснюється за допомогою означення дії віднімання. Учні повинні міркувати так: за означенням дії віднімання маємо рівності  і , які правильні за властивістю нуля щодо дії додавання. Отже, правильні також рівності  і .

Бажано, щоб після розв’язування вправ на віднімання двох натуральних чисел, учні усвідомили таке: дія віднімання неможлива в множині натуральних чисел, якщо зменшуване менше, ніж від’ємник, або дорівнює йому, то різниця завжди існує і дорівнює певному натуральному числу в першому випадку і нулю – в другому.

Повторення дії віднімання доцільно завершити нагадуванням типів задач, які розв’язуються за допомогою цієї дії.

Зміст дії множення натуральних чисел найкраще з’ясувати, виходячи з додавання кількох однакових чисел. Вже з початкової школи учні знають, що множенням натуральних чисел наливають додавання однакових доданків. На етапі повторення важливо, щоб учні після розв’язування певної кількості прикладів змогли виконати узагальнення і сформулювати означення для двох чисел  і  у вигляді: помножити число  на число  означає знайти суму  доданків, кожний з яких дорівнює . Доцільно звернути увагу учнів та те, що це означення поширюється лише на випадки натурального числа , відмінного від 1. Для добутку  потрібна спеціальна домовленість (означення), що . Так само і для дії .

Множення одиниці на натуральне число   (.)  і нуля на число  () обґрунтовують, виходячи з означення дії множення.

Слід приділити увагу попередженню помилок, яких частина учнів припускається, множачи на числа, які закінчуються нулями, або містять нулі всередині числа.

Перевіряють дію множення шляхом перестановки множників.

Основні закони множення, як і додавання треба повторювати, ілюструючи їх застосування для раціоналізації обчислень.

в) дробові числа.

Перше знайомство із звичайними дробовими числами 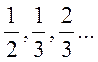 відбувається в 3-му класі паралельно із вивченням  натуральних чисел. Систематичне вивчення дробів починається у 5-му класі.