Пропонується, користуючись означенням ![]() записати координати
векторів
записати координати
векторів ![]()
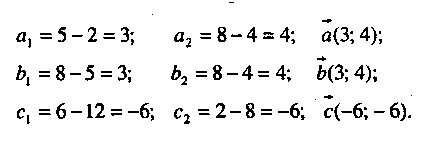 :
:
Внаслідок розв'язування цієї вправи учні дістали два факти:
1) виявилось, що координати рівних векторів однакові, а різних - різні;
2) учні визначають за допомогою формули відстані між двома точками довжину вектора а роблять висновок, що модуль вектора а дорівнює кореню квадратному із суми квадратів його координат.
Учні дійшли потреби довести необхідну і достатню
умови рівності двох векторів. Далі доцільно Я поставити перед учнями запитання:
чи можна визначати координати вектора за рисунком? Виявляється, що можна. Для
цього Я досить порахувати кількість клітинок під час руху від початку Я вектора
до кінця спочатку вздовж осі х, а потім - вздовж осі у. На наступному уроці
учням пропонується знайти за рисунком вже відомі координати вектора![]() і вектора
і вектора ![]() відтак
співвідношення між координатами векторів
відтак
співвідношення між координатами векторів![]() які
утворюють трикутник. Це підведе учнів до означення суми:
які
утворюють трикутник. Це підведе учнів до означення суми:
![]()
Помічаємо, що координати вектора АС є сумою координат векторів![]() які разом з вектором
які разом з вектором![]() утворюють трикутник.
утворюють трикутник.
Вивчення дій (операцій) над векторами. Вище наведено методичний варіант, за якого учні конкретно-індуктивним методом самостійно підводяться до формулювання означення суми двох векторів. Аналогічної· можна підвести і до формулювання означення різниці двох векторів через їх координати. Для векторного методу розв'язування задач важливо, щоб учні навчились вільно шляхом відповідних побудов знаходити·суму і різницю векторів. Тут виявляється ефективним алгоритмічний підхід - вміння знайти суму двох векторів за правилом трикутника·або правилом паралелограма.
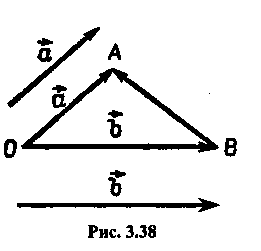
Задачу про побудову різниці двох векторів![]() корисно
розглянути теж двома способами.
корисно
розглянути теж двома способами.
1. Від довільної точки О відкланяються вектори ![]() (рис. 3.38). Позначається вектор
(рис. 3.38). Позначається вектор ![]() За правилом трикутника записується
векторна рівність
За правилом трикутника записується
векторна рівність![]() 3 означення різниці
векторів а і b (це такий
вектор, який у сумі з вектром b дає вектор а) випливає, ще
3 означення різниці
векторів а і b (це такий
вектор, який у сумі з вектром b дає вектор а) випливає, ще ![]() є
різницею векторів а і b, тобто
є
різницею векторів а і b, тобто ![]()
Звідси випливає плавило побудови вектора-різниці:
щоб спробувати вектор![]() треба:
треба:
а) перенести початки векторів α і h в довільну точку О;
б) позначити вектор-різницю с, у якого початком є кінець вектора-від'ємника (вектора 6), а кінець є кінцем вектора-зменшуваного (вектора а).
2. Другий спосіб побудови вектора-різниці
ґрунтується на ознаки ні протилежного вектора і доведеної теореми: ![]()
Звідси побудова: від довільної точки О
відкладається вектор 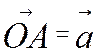 , а потім від точки А
вектор
, а потім від точки А
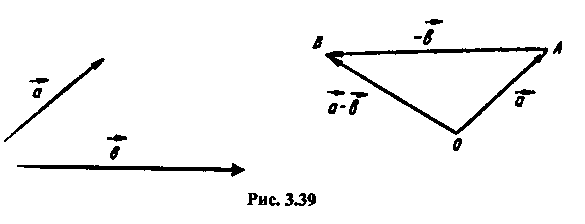
вектор 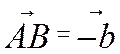 . Тому
. Тому 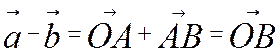 (рис.
3.39).
(рис.
3.39).
Слід мати на увазі, що в підручнику О.В.Погорєлова скалярний добуток двох векторів означається через їхні координати. І прийняте в багатьох посібниках за означення скалярного добутку твердження про властивість його дорівнювати добутку числових значень довжин на косинус кута між векторами υ підручниках доводиться. Введення скалярного добутку і поняття колінеарності векторів дає можливість розв'язувати різноманітні задачі, пов'язані з перпендикулярністю і паралельністю відрізків, метричні задачі на визначення довжин відрізків і величини кутів.
4.Векторний метод розв'язування задач.
До складу діяльності, спрямованої на використання векторного методу, входять такі специфічні розумові дії:
І) переформулювання відношень між фігурами з геометричної на мову векторів і обернена дія;
2) дії (операції) над векторами;
4)подання вектора у вигляді суми, різниці двох векторів, добутку вектора на число; перетворення векторних рівностей з використанням законів векторної алгебри і властивостей скалярного добутку;
5)перехід від співвідношень між векторами до співвідношень між їх довжинами.
Згідно з теорією поетапного формування розумових дій, важливе попереднє поетапне відпрацювання кожної розумової дії, що входить до складу діяльності щодо розв'язування задач векторним методом.
З векторним методом доведення геометричних тверджень і відповідним правилом-орієнтиром доцільно ознайомити учнів на прикладах доведення двох тверджень, з яких перше учні вміють доводити і без застосування векторів.
Внаслідок виділення суттєвого спільного в обох доведеннях учні колективно під керівництвом учителя можуть прийти до правила - орієнтира векторного методу доведення тверджень.
1. Виділити в формулюванні теореми (задачі) умови і вимоги, виконати рисунок. Сформулювати вимоги мовою векторів і, враховуючи їх, позначити вектори на рисунку.
2. Враховуючи умови і вимоги, скласти допоміжні векторні рівності. Для цього виразити, якщо це потрібно, вектори у вигляді суми або різниці інших векторів, або у вигляді добутку вектора на число. Перетворити одержані рівності і прийти до потрібної.
3. Перекласти одержану рівність на мову геометрії.
Найважчим для учнів є позначення векторів на рисунку. Досій а раціонального позначення векторів набувається на практиці, однак певні орієнтири в цьому дає аналіз формулювання теореми (задачі). Для формування навичок використання правила - орієнтира варто запропонувати учням розв'язати векторним методом
Таблиця 3.7 1

відомі з планіметрії твердження про властивість середньої лінії трикутника, про суму квадратів діагоналей паралелограма, про властивість діагоналей ромба, прямокутника.
Слід звернути увагу школярів на те, що векторний метод доведення теорем не універсальний, його зручно застосовувати для доведення паралельності і перпендикулярності прямих і відрізків, належності трьох точок одній прямій, подільності відрізка в даному відношенні для доведення співвідношень між довжинами відрізків і величинами кутів.
При розв'язуванні метричних задач, зокрема на визначення довжини відрізка і міри кута векторним методом, доцільно запропонувати учням відповідні алгоритми.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.