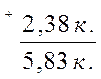Вирази та їх перетворення, страница 21

                                          ,

тобто десяткові дроби можна додавати подібно до того, як виконують додавання натуральних чисел: додають цілі до цілих, десяті до десятих, соті до сотих і т.д. Додавання зручно виконувати в стовпчик, пишучи числа так, щоб кома була під комою.

Потім треба розглянути додавання десяткових дробів з різною кількістю десяткових знаків, додавання десяткового дробу і натурального числа, після чого перейти до тренувальних вправ. Ці вправи поступово треба ускладнювати, розглядати додавання більше двох чисел, виконувати перевірку. Обов’язково треба показати (на прикладах), що для додавання десяткових дробів справджуються переставний і сполучний закони.

Аналогічно можна пояснити і віднімання десяткових дробів, причому це краще зробити відразу ж після пояснення додавання, щоб тренувальні вправи на додавання і віднімання розв’язувати одночасно.

Правило множення десяткових дробів зручно ілюструвати на прикладі знаходження площі прямокутника. Далі слід сформулювати правило і перейти до розв’язання тренувальних вправ. Звичайно, з наукової точки зору такі пояснення не можна вважати бездоганними, але й ускладнювати цей матеріал у 5 класі не треба. Так само на конкретних прикладах можна пояснювати і ділення дробових чисел. Слід зауважити, що ділення десяткових дробів можна виконувати двома способами: 1) замінювати і ділене і дільник натуральними числами; 2) замінювати тільки дільник натуральним числом.

г) вивчення додатних та від’ємних чисел.

Історія розвитку шкільного курсу математики свідчить про те, що спроба окремих авторів шкільних підручників і методичних посібників означити поняття від’ємного числа не привела до строго логічного означення. Тому це поняття доцільно вводити описово в тісному зв’язку з потребами практики та інтерпретацією на координатній прямій.

Найвдалішим є підхід, коли від’ємні числа вводяться для позначення числових значень величин, які змінюються у двох протилежних напрямках. Пояснення починається з прикладів, які приводять учнів до висновку, що для позначення числових значень числових величин треба вказати напрямок зміни величини.

Щоб позначити числом значення величин, які можуть змінюватися у двох протилежних напрямках, було введено від’ємні числа. Всі відомі до цього натуральні і дробові числа назвали додатними.

Від’ємні числа стали записувати зі знаком “-”, наприклад: -7, -9,4. перед додатними числами домовилися ставити знак “+” або писати їх без знаку. Число 0 не належить ні до додатних, ні до від’ємних чисел.

Додатні і від’ємні числа зручно зображувати на координатній прямій.

Відтак вводять поняття координатної прямої, продовжуючи ліворуч відомий учням координатний промінь. Бажано, щоб у класі була демонстраційна координатна пряма, а в кожного учня – модель такої прямої, виготовлена зі звичайної дерев’яної або пластмасової лінійки з наклеєною шкалою, де позначені додатні і від’ємні числа із просвердленими отворами в точках поділу шкали.

Доцільно звернути увагу учнів на те, що коорднитних прямих можна побудувати безліч залежно від вбору одиниць відліку.

Після введення поняття координати точки учні розв’язують за допомогою моделі координатної прямої і відповідних записів в зошиті вправи на позначення на координатній прямій точок за їх координатами і обернені вправи – за позначеною на прямій точкою визначають її координати. Розв’язуються різноманітні вправи, пов’язані з поняттям відстані між двома точками, заданими їх координатами.

Під час введення поняття модуля числа формулюється геометричне означення модуля через поняття відстані  від початку відліку точки, що зображує число. У деяких посібниках властивість модуля числа для невід’ємного числа бути самим числом, а для від’ємного – протилежним числом називають також означенням модуля. Оскільки учні вже знайомі з буквеним записом законів арифметичних дій, з формулами, то можна після усного  розв’язування вправ та визначення модуля чисел узагальнити властивість модуля:

 

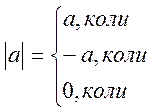
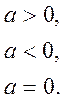
Порівняння нових чисел треба ілюструвати на координатній прямій.

Відомо, що правило додавання від’ємних і додатних чисел у теоретичних курсах вводять за означенням. У школі до потрібного правила приходять, розв’язуючи задачу на знаходження результату двох послідовних змін якоїсь величини. При цьому допускають, що задачі, які при додатних значеннях величин розв’язуються додаванням, повинні розв’язуватись додаванням і при від’ємних значеннях цих величин. Найчастіше розглядають  задачу про послідовну зміну температури.

-  Якщо за першу половину дня температура змінилася на , а потім ще на , то всього температура змінилась на , бо 2+3=5.

-  Якщо за першу половину дня температура повітря змінилась на , а потім ще на , то всього температура, очевидно, змінилась на . Отже, (-2)+(--3)=-5.

-  Якщо за першу половину дня температура повітря змінилась на , а за другу – на , тобто спочатку підвищилась на , то очевидно, всього вона змінилась на . Отже, (+6)+(-2)=4.

Аналізуючи подібні рівності, можна сформулювати відповідні правила:

3.  Щоб додати два від’ємних числа, треба: 1) додати модулі доданків; 2) перед одержаним числом поставити знак “-”.

4.  Щоб додати два числа з різними знаками, треба: 1) від більшого модуля відняти менший; 2) поставити знак числа з більшим модулем.

Правила доцільно закріпити розв’язуванням певного набору вправ.

У разі віднімання принциповим положенням для обчислень і виконання тотожних перетворень є заміна дії віднімання дією додавання числа, протилежному від’ємнику. Підвести учнів до цього способу можна різними способами. Один з них наведено у підручнику  [ Нурк 6 кл.]. він зводиться до виконання перетворень рівняння х+5=2, з якого знаходять х=2-5. зазначається, що виконати таке віднімання ми поки що не можемо. Проте, додавши до обох частин даного рівняння число (-5), дістанемо х+5+(-5)=2+(-5).

Звідси  х=2+(-5); х=-3. після перевірки того, що число –3 є коренем даного рівняння роблять висновок, що значення х з рівностей х=2-5 і х=2+(-5) можна прирівняти. Отже, дістанемо рівняння 2-5=2+(-5).