Вирази та їх перетворення, страница 37

Крім поняття декартових координат в цій темі вводяться такі нові для учнів поняття: рівняння фігури в декартових координатах, кутовий коефіцієнт прямої, синус, косинус, тангенс кута від 0° до 180°.

При введенні першого поняття треба спиратися на відомі з курсу алгебри 7 класу поняття рівняння з двома невідомими, лінійного рівняння з двома невідомими ах + by = с. Учні повинні пригадати, що графіком такого рівняння може бути пряма (за умови, що хоча б один з коефіцієнтів а або b не дорівнює нулю), вся координатна площина приі порожня множина точок за

У курсі геометрії ставиться мета довести, що будь-яка пряма в декартових координатах х і у має рівняння вигляду  Треба, щоб учні розуміли, що відоме їм з курсу алгебри лі­нійне рівнянняпринципово не відрізняється від рівняння

Якщо пригадати відоме з курсу алгебри 7 класу поняття про систему двох лінійних рівнянь з двома невідомими, означення розв'язку системи і графічний спосіб її розв'язання, то учні самі дійдуть відомого їм висновку щодо координат точки перетину прямих. Поняття кутового коефіцієнта прямої важливе, з погляду перспективних зв'язків, з поняттям геометричного змісту похідної, яке вводиться у 10 класі.

Введення означеньбудь-якого кута від 0 до 180° потребує мотивації. Однак спочатку треба пригадати означення синуса, косинуса і тангенса гострого кута через відношення сторін в прямокутному трикутнику. Запроваджені раніше означення дали можливість розв'язувати прямокутні трикутники. Проте в геометрії, фізиці, геодезії, техніці та інших галузях доводиться розв'язувати і косокутні трикутники, де кути можуть змінюватись від 0 до 180°. У зв'язку з цим виникає потреба означити тригонометричні функції і для таких кутів. Виявляється, що це зручно зробити за допомогою декартових координат. Далі вводяться означення за допомогою кола радіуса, розміщеного в координатній площині.

Після запровадження означеньдля кутів  для tg α виключається) слід навчити учнів знаходити їх значення за допомогою таблиць і мікрокалькулятора. В умовах роботи за підручником О. В. Погорєлова не передбачене вивчення теорем в темі «Декартові координати на площині», проте доводиться ряд тверджень, яких немає під рубрикою «теорема». Основні з них чотири: виведення формул координат середини відрізка, довжини відрізка, рівняння кола і ведення відомого, але принципово важливого факту, графіком лінійної функції є пряма і її властивість щодо точок І перетину з колом, даються в плані ознайомлення і виступають як вправи на застосування методу координат.

Перед доведенням формул координат середини відрізка повторити теорему Фалеса і спосіб визначення відстань між двома точками на прямій за їх координатами, означення мла. Досвід показує, що для деяких учнів незрозумілим є перехід від рівності до двох рівностей:   . Тому доцільно попередньо розв’язати усно такі вправи.

1)  Нехай =2. Знайти х.

2)  Учні знаходять: х= 2 або x = -2.

3)  Нехай | χ | = а, де а > 0. Знайти х.
Учні знаходять: x-а або х = -α.

3) Нехай. Які дві рівності випливають з даної рівності?

Учні вказують дві рівності: х-х₁=х-х₂ або х-х₁= - (х-х₂). Оскільки за умовою х₁=х₂  , то перша рівність не, може виконуватися. Отже, виконується друга рівність, з якої знаходимо х.

Справді,  х-х₁= - х+х₂ , звідки 2х = х₁+х₂,

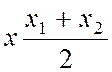
Система задач теми в основному спрямована на закріплення  введених понять і використання доведених формул.

2. Вектори  на площині

 Ідея вектора - одна з фундаментальних ідей на площині сучасної математичної науки та її застосувань. На векторній основі зараз будуються лінійна алгебра, аналітична і диференціальна геометрія, теорія багатовимірних просторів. Вектори широко застосовуються в сучасній фізиці, технічних науках. Тому природно, що в 50-х роках XX ст. на початку всесвітнього руху за реформу шкільної математичної освіти у всіх розвинутих країнах була висловлена одностайна думка - впровадити ідею вектора в шкільну математику, При цьому пропонувалося два підходи.

1.  Крайні модерністи (Ж. Дьєдонне, Л. Фелікс, Г. Шоке) наполягали на тому, щоб зробити ідею вектора базисною ідеєю шкільного курсу і, зокрема, курс геометрії будувати на основі ідеї векторного простору, наприклад, використовуючи аксіоматику Вейля.

2.  У колишньому СРСР А. М. Колмогоров, О. І. Маркушевич, які очолювали перебудову змісту шкільної математичної освіти, дотримувались поміркованого підходу і пропонували не розглядати ідею вектора як базисну і не будувати навіть певний розділ геометрії на векторній основі. Разом з тим передбачалось ввести поняття вектора і необхідний апарат векторної алгебри із загальноосвітньою метою та використовувати вектори як апарат для доведення теорем і розв'язування задач геометрії, фізики. Спробу реалізувати такий погляд здійснено в посібниках з геометрії за редакцією А. М. Колмогорова та 3. А. Скопця , а також у паралельних підручниках геометрії .

У зв'язку зі зменшенням кількості годин на вивчення математики в школі базова програма й автори чинних паралельних підручників геометрії не ставлять за мету систематично використовувати векторний метод при доведенні теорем і розв'язуванні задач, а передбачають вивчати вектори із загальноосвітньою метою і послуговуватися ними лише для розв'язування найпростіших стандартних задач. Безперечно, в старших класах фізико-математичного профілю, спеціалізованих школах і класах з поглибленим вивченням математики, на факультативах векторний метод має широко застосовуватися.

За чинною програмою і проектом нової програми з математики вектори передбачено вивчати в два етапи: спочатку вивчаються вектори на площині, а потім - у просторі. У підручнику О. В. Погорєлова у 8 класі крім основних понять, що стосуються векторів, вивчаються всі операції над векторами (додавання, віднімання, множення вектора на число і скалярний добуток двох векторів, розкладання векторів по координатних осях). Дещо інше місце вектори посідають у підручнику Л. С. Атанасяна та ін. Тут вектори починають вивчатися у 9 класі, що звужує можливості їх застосування в геометрії і фізиці.