На
таких вправах учні ще раз переконуються, що всі відповідні значення виразів ![]() і
і ![]() рівні; отже ці
вирази тотожні. Після пояснення розглядуваної тотожності одразу можна перейти
до розв’язання тренувальних вправ. Спочатку краще записувати і проміжні
перетворення і лише згодом слід пропонувати одразу писати відповідь.
рівні; отже ці
вирази тотожні. Після пояснення розглядуваної тотожності одразу можна перейти
до розв’язання тренувальних вправ. Спочатку краще записувати і проміжні
перетворення і лише згодом слід пропонувати одразу писати відповідь.
Тільки після того, як учні засвоять основне: добре знатимуть формулу і навчаться нею для множення многочленів, можна розглянути і кілька інших питань, пов’язаних з нею. Насамперед – про використання цієї формули для усних обчислень.
Треба домогтися, щоб кожен учень добре запам’ятав формули і вмів користуватись ними. Адже спостерігаються випадки, коли окремі учні хоч і знають всі п’ять формул, але користуватися ними не вміють. Їм інколи допомагають такі записи, в яких компоненти позначені не буквами, а різними “віконцями”, наприклад:
( + O) ( - O) = 2 - O2.
Написавши таку “формулу”, вчитель пропонує учневі: “Запиши в кожному прямокутнику 2m, а в кожному колі x3 і розстав показники степенів і знаки”.
Зрозуміло, щоб виробити навички безпомилково і швидко користуватися формулою, треба розв’язати немало прикладів. Бажано пропонувати учням доводити тотожності, розв’язувати рівняння, а також обчислювати значення виразів при даних значеннях букв, спрощення виразів, виведення формул наближених обчислень.
Під час підсумкового повторення теми доцільно назвати ще раз всі види тотожних перетворень цілих виразів та їх можливе застосування.
2.Тотожні перетворення раціональних виразів.
Як відомо, раціональними називають вирази, які не містять ніяких інших дій, крім додавання, віднімання, множення, ділення і піднесення до степеня з цілим показником.
До тотожних перетворень раціональних виразів, відмінних від цілих, які вивчаються у 8 класі, належать скорочення раціональних дробів, множення, піднесення до степеня з натуральним показником, ділення дробів і тотожні перетворення раціональних виразів, до складу яких входять цілі і дробові вирази.
З дробових раціональних виразів слід виділити раціональні дроби. Так як їх починають вивчати, ще не ознайомившись з ірраціональними виразами, то учні говорять просто: дроби.
Дробом
називають кожен вираз виду ![]() , де
, де ![]() і
і ![]() - довільні
вирази.
- довільні
вирази.
Ввівши поняття дробу, треба зупинитися на знаходженні їх числових значень. Учні повинні вміти знаходити числові значення дробу при будь-яких допустимих значеннях змінних. Вводити поняття області допустимих значень у 8 класі не рекомендується, але термін “допустимі значення змінної” учні повинні розуміти.
Обов’язково треба уточнити (розширити) поняття тотожних виразів і дотримуватись вже такого означення. Рівність, справедлива при всіх допустимих значеннях змінних, що входять до неї, називається тотожністю.
Далі
слід розглянути основну властивість дробів (рівність 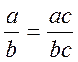 справджується при будь-яких
значеннях
справджується при будь-яких
значеннях ![]() ,
, ![]() , і
, і ![]() , де
, де ![]() ) і показати
учням, як на її основі можна скорочувати дроби.
) і показати
учням, як на її основі можна скорочувати дроби.
Типовою
помилкою під час скорочення раціональних дробів є така: 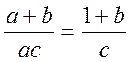 .
.
Під
час виконання дій над дробовими трапляються помилки на зразок: 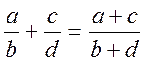 ;
;  .
.
Одним із способів зменшення кількості названих помилок є обчислення даного й одержаного після “перетворення” виразу.
Практика свідчить про те, що для уникнення помилок треба зробити пряму вказівку про неприпустимість таких перетворень ще при введенні нового матеріалу і пояснити учням, чому саме таке перетворення є помилковим.
Перетворення суми і різниці раціональних дробів з різними знаменниками спирається на вміння знаходити найпростіший спільний знаменник.
Доцільно сформулювати правило (алгоритм відшукання найпростішого спільного знаменника: 1)скласти добуток найменшого спільного кратного модулів коефіцієнтів знаменників даних дробів і степенів кожної змінної з найбільшим показником, з яким змінна входить до знаменників цих дробів; 2) знайти додаткові множники даних дробів; для цього досить записати спільний знаменник у вигляді добутку двох співмножників, з яких один - знаменник даного дробу, тому другий буде додатковим множником його; 3) знайти добуток чисельника кожного дробу на додатковий множник і записати спільний знаменник.
Аналогія
у виконанні дій множення і ділення раціональних дробів і звичайних дробів як
числових виразів полегшує сприйняття учнями цих тотожних перетворень. Разом з
тим, виконуючи перетворення, треба враховувати, що два дробово-раціональні
вирази називаються тотожно рівними, якщо вони мають одну й ту ж саму область
визначення і на ній тотожно рівні. Тому, перетворюючи у дріб добуток двох
дробів 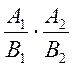 ,
дістанемо дріб
,
дістанемо дріб 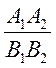 ,
який має ту саму область визначення, що й добуток
,
який має ту саму область визначення, що й добуток 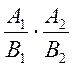 . Отже, ці вирази тотожно рівні.
. Отже, ці вирази тотожно рівні.
Частка
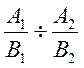 визначена для тих
значень змінних, для яких жоден з цілих виразів
визначена для тих
значень змінних, для яких жоден з цілих виразів ![]() ,
, ![]() і
і ![]() не стає таким, що дорівнює нулю.
Областю визначення дробу
не стає таким, що дорівнює нулю.
Областю визначення дробу 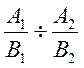 є множина значень змінних, за яких
не перетворюються в нуль цілі вирази
є множина значень змінних, за яких
не перетворюються в нуль цілі вирази ![]() і
і ![]() . Це означає, що область визначення
виразу
. Це означає, що область визначення
виразу 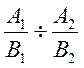 є
підмножиною області визначення дробу
є
підмножиною області визначення дробу 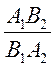 або збігається з нею, і ці вирази
тотожно рівні на області визначення частки двох дробів.
або збігається з нею, і ці вирази
тотожно рівні на області визначення частки двох дробів.
Основною метою перетворення раціональних виразів, до складу яких входять цілі і дробові вирази, є перетворення їх у дріб, чисельник і знаменник якого є цілими раціональними виразами. Може трапитись так, що одержаний внаслідок перетворення дріб не тотожно рівний даному раціональному виразу внаслідок зміни області визначення. У таких випадках у відповіді разом зі знайденим дробом треба зазначити множину, на якій розглядається цей дріб.
3.Тотожні перетворення ірраціональних виразів.
Тотожні перетворення ірраціональних виразів вивчаються в школі відповідно до діючої програми у 2 етапи: у 8 класі учні ознайомлюються з квадратними коренями, їх властивостями і перетвореннями виразів, що містять квадратні корені, у 9 класі дістають відповідні знання і вміння стосовно кореня n–того степеня з дробовим показником. Перетворення виразів, що містять корені, знаходять широке застосування при вивченні математики в середній школі: під час розв’язування геометричних задач, при розгляді питань, пов’язаних з дослідженнями функцій, при ознайомленні з похідною та її застосуваннями. Крім перетворення добутків, степенів радикалів і спрощення їх найбільш поширеними перетвореннями, які при цьому доводиться виконувати, є такі:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.