Вирази та їх перетворення, страница 7

Паралельно із методикою вивчення функції , розглянемо й методику вивчення  . Під час вивчення цих функцій у 7-му класі можна навести приклади залежності між змінними, які приводять до цих функцій (залежність площі квадрата від довжини його сторони S=a², залежність об’єму куба від довжини його сторони V=a³ )/

Почати вивчення функцій  і  слід з побудови графіка за допомогою таблиці, а потім прийти до узагальнення. Учні заповнюють таблицю для цілочисельних значень аргументу, а утворені точки сполучають плавною лінією. Учитель пояснює, що криву функції  називають параболою (функції  - гіперболою) і показує їх точне зображення (на таблиці, плакаті).

Можна запропонувати учням, ще до заповнення таблиць і побудови графіків дослідити їх властивості і передбачити деякі особливості в розташуванні графіків на основі відомих учням властивостей виразів х² і х³ . Справді, обидва графіки мають пройти через початок координат, оскільки при х=0 у=0.

При  для функції  у завжди додатне. Це означатиме, що графік лежатиме вище осі х, крім точки (0;0).

Для функції  при   і  , а при    за властивістю степеня з непарним показником. Це означає, що при графік міститиметься в першій координатній чверті, а при  - у третій чверті.

Підготовкою до вивчення властивостей зростання і спадання функцій є усні вправи на встановлення тих ділянок області визначення функції , де при зростанні аргументу х значення функції теж зростають  і де при зростанні значення х значення у зменшується. За графіком функції  учні можуть встановити, що на всій області визначення при зростанні х значення у зростає.

Обов’язковими є такі знання про властивості графіка функції :

-  весь графік функції  розмішений у верхній координатній півплощині;

-  тільки одна його точка лежить на осі х;

-  графік симетричний відносно осі у;

-  кожна гілка параболи – графіка функції  - нескінченна.

Мікрокалькулятор дасть можливість переконатися в тому, що при досить близьких до нуля значеннях аргументу графіки функцій ,  майже збігаються з віссю х.

Для зручності виконання побудов та застереження від неправильних побудов використовують  шаблони графіків. Для прискорення побудови графіків бажано мати спеціальну дошку з координатною сіткою.

в)  функція .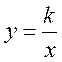

Вивчення цієї функції доцільно починати з розгляду конкретних прикладів.

1.  Площа прямокутника, виміри якого дорівнюють х і у виражається формулою ху=к , .

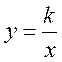2.  Відстань між двома пунктами дорівнює 150 м, х – швидкість руху, м/с, у – час руху, с. Тоді .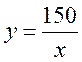

У цих прикладах змінні х та у набувають лише додатних значень і пов’язані між собою так, що із збільшенням значень х у кілька разів відповідні значення у зменшуються в стільки ж разів. Такі змінні називають обернено пропорційними.

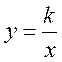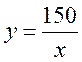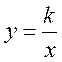Формулами ,  задаються функції: функція, яку можна задати формулою виду , де х – незалежна змінна і к – число, що не дорівнює нулю, називається оберненою пропорційністю.

Областю визначення функції 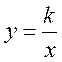 є множина всіх дійсних чисел, відмінних від 0. це випливає з того, що вираз 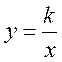 має зміст при всіх значеннях х, де .

Далі розглядається графік ф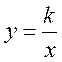ункції  для k>0 і k<0 . підкреслюється, що графіком функції 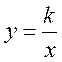 є дві криві лінії, що утворюють одну геометричну фігуру, яка називається гіперболою. Для побудови графіків кількох функцій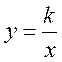 при додатних і від’ємних х учні повинні зробити висновок щодо розташування гіперболи у відповідних координатних чвертях залежно від знака к, характеру зміни значень функції із зростанням значень аргументу.

Поступово учні засвоюють властивості і функці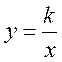ї  для k>0 і k<0  у такому формулюванні:

1.  Функція 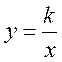 , де к – додатне число, набуває від’ємних значень, коли  і додатних значень, коли .

2.  Функція 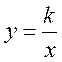, де к – додатне число, спадає на кожному з проміжків (-¥; 0) (0; +¥).

3.  Функція 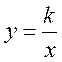, де к – від’ємне число, набуває додатних значень, якщо , і від’ємних значень, якщо .

4.  Функція 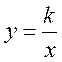, де к – від’ємне число, зростає на кожному з проміжків (-¥; 0)  і  (0; +¥)..

Для кращого сприйняття цих властивостей учнями доцільно, щоб вони колективно склали таблицю, де ці властивості пов’язувалися б з відповідними графіками.

У 10 класі після введення означень зростаючої, спадної, парної і непарної функцій треба знову звернутися до  властивостей функції 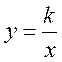, довести її аналітично, послуговуючись відповідними означеннями.

г) Функція , де .

Квадратичною функцією називають функцію, яку можна задати формулою виду  , де х – незалежна змінна, a, b і c – деякі числа, причому .

При вивченні квадратичної функції у 9-му класі на етапі мотивації неважко навести  при клади залежностей, які задаються функцією , котра є окремим випадком квадратичної, і важче підібрати аналогічні приклади для загального вигляду функції. Проте такий приклад є. У курсі фізики учні вивчають формулу положення тіла відносно системи координат у будь-який момент часу t: за прискореного руху 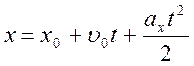, де  - початкова координата;  - початкова швидкість (проекція вектора швидкості на вісь х);  - прискорення (проекція вектора прискорення на вісь х).

Найскладнішим для сприймання учнями є навчальний матеріал, що стосується побудови графіка квадратичної функції загального вигляду ,. Тому не випадково учнів готують до цього шляхом послідовного розгляду питань побудови графіків функцій , , , спираючись на побудову відомого графіка функції . З метою актуалізації опорних знань і вмінь треба повторити розв’язування вправ на виділення квадратного двочлена з тричлена  за певних числових значень a,  b,  c і лише після цього перейти до розв’язування задачі в загальному вигляді.

д)     

У шкільних підручниках функція   розглядається у зв’язку з вивченням квадратних коренів. Співставляються дві задачі: знайти площу S квадрата за його стороною а і відповідно знайти сторону а  квадрата, якщо відома його площа S. Підкреслюється, що формулами   , де  і  задаються функціональні залежності між одними й тими ж самими змінними проте у першому випадку незалежною змінною є сторона квадрата, а другому – площа.