Вирази та їх перетворення, страница 3

Отже, у сучасному розумінні алгебру можна визначити як на-Іуку про системи об'єктів тієї чи іншої природи, в яких встановлено операції, що за своїми властивостями більш-менш схожі на додавання і множення чисел. Ці операції називаються алгебраїчними. Алгебра класифікує системи об'єктів із заданими на них алгебраїчними операціями за їх властивостями і вивчає різні задачі, які природно виникають в цих системах, включаючи і задачу розв'язування і дослідження рівнянь. Остання в нових системах об'єктів дістає новий зміст. Наприклад, розв'язком рівняння І може бути вектор, матриця, оператор тощо.

2. Зміст навчання алгебри основної школи.

До шкільного курсу алгебри входить не тільки суто алгебраїчний матеріал, а й той, що стосується математичного аналізу (наприклад, вчення про функцію). Навчальний матеріал курсу групується навколо п'яти основних змістових ліній.

1. Розвиток поняття про число. Починаючи вивчення курсу • алгебри, учні вже знають множину раціональних чисел. У 8 класі І вводяться ірраціональні числа, що утворюють разом з раціональними числами множину дійсних чисел. У старших класах з поглибленим вивченням алгебри і початків аналізу множина дійсних чисел розширюється до множини комплексних чисел. І У 8 класі вивчаються наближені обчислення, які теж можна від-1 нести до цієї змістової лінії.

2. Тотожні перетворення виразів. У курсі алгебри ця лінія дістає найбільшого розвитку. У 7 класі вивчаються прямі й обернені перетворення цілих виразів, у 8 класі - дробових і тих ірраціональних виразів, які пов'язані з квадратним коренем. У 9 класі розглядались перетворення тригонометричних виразів. Досвід показує, що вивчення останньої теми відбувається дещо формально, оскільки цей матеріал не застосовується для розв'язування тригонометричних рівнянь. До 10 класу, де ці рівняння вивчаються, учні встигають забути основні тригонометричні тотожності і втратити набуті навички перетворень тригонометричних виразів. Тому нова програма передбачає перенесення цієї теми до 10 класу, а за рахунок звільненого навчального часу пропонується ознайомити учнів з початковими відомостями статистики, елементами комбінаторики і теорії ймовірностей.

3. Рівняння і нерівності. У 7 класі учні далі розв'язують лінійні рівняння, вводяться їх означення і загальний вигляд. Завершується вивчення алгебри в 7 класі введенням поняття системи рівнянь з двома невідомими. У 8 класі вивчаються квадратні рівняння і застосування їх до розв'язування текстових задач та дробові рівняння, які зводяться до квадратних. У 9 класі триває розв'язування квадратних рівнянь і таких, що зводяться до них, зокрема біквадратних; вводяться системи рівнянь, серед яких є рівняння другого степеня. Вивчення числових нерівностей, лінійних нерівностей з однією змінною та їх систем передбачено у 8 класі, а нерівностей другого степеня та дробових нерівностей -у 9 класі.

4. Вчення про функцію. На основі функціональної пропедевтики, яка проводилась в 1-6 класах, явне введення функції, її загального поняття відбувалось за програмою в 7 класі. Проте досвід викладання алгебри останніми десятиріччями свідчить про те, що програма 7 класу виявляється перевантаженою новим для учнів навчальним матеріалом, який закладає основи алгебри. Тому за новою програмою самостійна тема «Елементарні функції» передбачена у 8 класі. Тут учні повинні дістати уявлення про функції як математичні моделі залежності між величинами й об'єктами будь-якої природи. На прикладах прямої й оберненої пропорційності передбачається ввести поняття про основні способи задання функції. Передбачено також вивчати властивості функцій 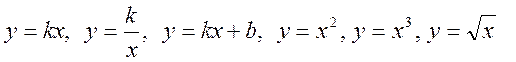, їх графіки, табличні способи задання. У зв'язку з останнім питанням передбачено ознайомити учнів з використанням і аналізом різних дослідних даних, поданих у таблицях, з метою розвитку і наступного формування статистичних уявлень.

5. Елементи статистики, комбінаторики і теорії ймовірностей. Ця нова змістова лінія включена до нової програми і набуде дальшого розвитку в курсі алгебри і початків аналізу. : Мета вивчення алгебри в основній школі - вдосконалення обчислювальних навичок, поглиблення розуміння буквених виразів, ах видів і тотожних перетворень цілих, дробових, ірраціональних виразів; поглиблення і розширення апарату рівнянь і нерівностей як основного засобу математичного моделювання прикладних задач; формування уявлення про функцію, вивчення властивостей елементарних функцій; ознайомлення з початковими відомостями про статистику; введення елементів комбінаторики і теорії ймовірностей.

В результаті вивчення курсу учні повинні оволодіти такими знаннями й уміннями, що задають обов'язковий рівень підготовки:

мати уявлення про ірраціональні числа, дійсні числа, наближене значення числа і величини; знати означення квадратного кореня, абсолютної і відносної похибки; правила наближених обчислень без строгого врахування похибок (правила підрахунку правильних цифр);

виконувати арифметичні дії над точними і наближеними значеннями (у тому числі і з використанням мікрокалькулятора), робити прикидку й оцінку точності результатів обчислень;

розуміти суть одночлена, многочлена, алгебраїчного дробу, дробового виразу; знати формули скороченого множення, правила виконання основних видів тотожних перетворень виразів, зазначених у програмі;

виконувати тотожні перетворення цілих і раціональних виразів (у тому числі за допомогою формул скороченого множення), ірраціональних виразів, що містять квадратні корені;

розуміти суть числових нерівностей і знати їх властивості, розуміти суть нерівності зі змінною, лінійного, квадратного, раціонального рівняння і нерівності;

вміти розв'язувати зазначені в програмі види рівнянь і нерівностей, систем рівнянь і нерівностей, текстові задачі методом рівняння;

вміти розрізняти види функцій, зазначених у програмі, виражати на простих прикладах залежності між змінними; знаходити значення функцій, заданих формулою, таблицею, графіком;

будувати і читати графіки функцій, зазначених у програмі;