Вирази та їх перетворення, страница 38

Базова програма вимагає в 8-9 класах мати уявлення про вектор, рівні вектори, вміти виконувати операції над векторами, передбачені програмою, і використовувати вектори до розв'язування нескладних стандартних задач (обчислення довжин відрізків і міри кутів, додавання і віднімання векторів, множення вектора на число, скалярний добуток векторів).

Про різні можливі означення вектора. У зв'язку з введенням векторів у шкільний курс насамперед постало питання: яке означення вектора взята в курсі геометрії? У журналі «Математика в школе» з цього приводу спеціально друкувались статті (див., зокрема: Γ. Π. Бевз. Об определении понятия «вектор» // Математика в школе, 1980, №2; А. Д. Александров. Так что же такое вектор? // Математика в школе, 1984, № 5). Як зазначає О. Д. Александров у згаданій вище статті, питання «Що ж таке вектор?», «Яке означення правильне?» не точні. Відповіді на ці питання такі: вектор - це те, що називають вектором, і правильне означення те, яке прийняте, якщо тільки воно свідоме і не містить у собі суперечності. Точніше запитати не що таке вектор, а що називають вектором або що слід називати вектором, щоб означення було осмисленим, не призводило до плутанини і було плідним у застосуваннях. Γ. Π. Бевз звернув увагу на те, що в фізиці і геометрії розглядають різні поняття вектора. У фізиці розрізняють зв'язані і ковзні вектори.

Зв'язані вектори звуться рівними, якщо вони мають не тільки рівні модулі й однакові напрями, а й спільну точку прикладання.

Клас рівних між собою векторів, розміщених на одній прямій, називають ковзними векторами. Отже, ковзний вектор визначається трьома елементами: прямою, напрямом і довжиною.

У геометрії розглядаються вільні вектори, тобто такі, для яких суттєвим є лише довжина і напрям. Наведемо приклад. Якщо маємо дві зчеплені шестірні (рис. 3.36), то вектори О₁Р₁ і O₂F₂, з погляду фізики, різні, бо сили, що зображуються ними, обертають шестірню в протилежних напрямах, 3 погляду геометрії - всі

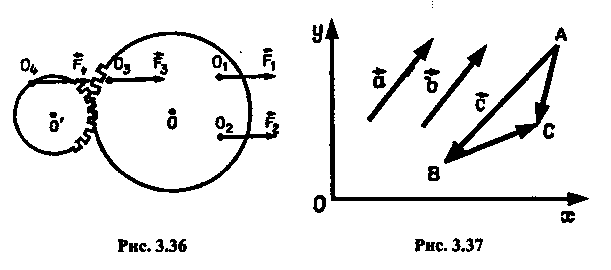
чотири вектори O₁F₁, O₂F₂, O₃F₃. O₄ F₄  зображують той самий вектор. Вільні вектори застосовують і в фізиці. Наприклад, швидкість і прискорення твердого тіла, що рухається поступально, - вільні вектори.

У навчально-методичній літературі трапляються різні означення вільних векторів. Вектори трактуються як:

1)напрямлений відрізок прямої евклідового простору, в якого один кінець (точка А) називається початком вектора, а другий кінець (точка В) - кінцем вектора;

2)впорядкована пара точок;

3)клас еквівалентних напрямлених відрізків;

4)паралельне перенесення;

5)впорядкована пара, трійка,..., n-чисел.

Множини об'єктів, що відповідають цим трактуванням, ізоморфні одна одній. Кожне з наведених трактувань є інтерпретацією більш загального абстрактного поняття вільного вектора, означення якого формулюється в теоретичних курсах геометрії: будь-яку множину об'єктів, що задовольняє перші вісім аксіом системи Вейля, називають множиною векторів, а будь-який елемент цієї множини - вектором. У школі з дидактичних міркувань звичайно розглядають одну з інтерпретацій. У посібниках вектор означається як паралельне перенесення, а в підручниках його трактують як напрямлений відрізок. О. Д. Александров у згаданій вище статті критично проаналізував різні означення векторів і звернув увагу на те, що, даючи означення через напрямлений відрізок, треба спочатку дати означення напрямленого відрізка і рівності напрямлених відрізків, а відтак сформулювати означення: вектором в геометрії називають напрямлений відрізок, що розглядається з точністю до вибору початку, тобто рівні один одному напрямлені відрізки вважаються представниками або зображеннями того самого вектора.

3.Методика введення основних понять теми.

З метою мотивації запровадження поняття «вектор» доцільно нагадати учням, що з поняттям векторних величин вони стикались раніше, в 7 класі, в курсі фізики. У підручнику фізики векторними називають величини, які крім числового значення (модуля) мають напрям. Наприклад, сила - векторна величина. На рисунках силу зображують у вигляді відрізка прямої із стрілкою на кінці, яка вказує напрям. Взагалі поняття вектора в геометрії ) виникло як математична абстракція об'єктів, що характеризуються величиною і напрямом на відміну від скалярних величин, які характеризуються лише числом. Проте не будь-яка величина, що характеризується модулем (числовим значенням при даній одиниці) і напрямом, є вектором. Наприклад, потік машин на вулиці міста можна виміряти кількістю машин за 1 год, і цей потік має напрям. Однак такі величини не додаються як вектори, наприклад m правилом трикутника або паралелограма.

У темі, присвяченій векторам на площині, вводиться значна кількість нових для учнів понять - абсолютна величина (або модуль вектора), нульовий вектор, рівні вектори, координати вектора, кут між ненульовими векторами, колінеарні вектори та ін. Викладений в підручнику О. В. Погорєлова теоретичний матеріал, що стосується векторів на координатній основі, вигідно відрізняється чіткістю, економністю, простотою доведень законів дій над векторами. Водночас тут мало геометричних ілюстрацій, які розвивали б просторові уявлення і уяву, вправ на побудову. Одним з найважливіших для подальшого викладу теоретичного матеріалу є поняття про координати вектора. Не можна обмежуватися лише формальним введенням означення цього поняття. Доцільно мотивувати потребу в ньому, дати учням наочне уявлення про координати вектора на координатній площині. Розглянемо один з можливих методичних варіантів запровадження поняття координат вектора.

Учитель звертає увагу учнів на те, що сьогодні на уроці вони знайомляться з новим для них поняттям - координатами вектора. Координати вектора, як і координати точки, дають можливість визначати положення вектора на координатній площині. Координати вектора дадуть змогу означити дії (операції) над векторами, довести їхні властивості і застосувати до розв'язування задач, а також встановити зв'язок між геометричними закономірностями в розміщенні векторів і арифметичними закономірностями між їхніми координатами, навпаки. Учням пропонується розглянути положення трьох векторів  a, b, c на координатній площині і порівняти їх розміщення. Учні помічають, що вектори а і b рівні (мають рівні модулі і однаково напрямлені). Вектори а і с  - різні і за довжиною, і за розміщенням на координатній площині. Щоб схарактеризувати помічені закономірності за допомогою чисел, введемо координати векторів, які задаються за допомогою координат початку і кінця вектора. (Вводяться означення координат вектора. символічні позначення.