Линейные цепи с сосредоточенными параметрами. Линейные четырехполюсники. Колебательные контуры (5-7 главы учебника "Радиотехнические цепи и сигналы" под ред. К.Е.Румянцева)

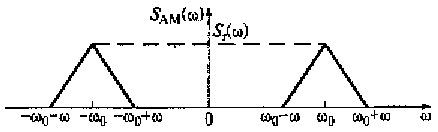
Рис. 4.8. Спектральная плот­ность AM-сигнала

         Обычно спектральная плотность управляющего сигнала распо­лагается в узком диапазоне частот (разговор по телефонной ли­нии разборчив, если спектр этого сигнала лежит в диапазоне ча­стот от 300 до 3400 Гц). При формировании AM-колебания спектр управляющего сигнала переносится в область частоты ω₀ несущего колебания, но при этом его ширина сохраняется. Таким обра­зом, в окрестности частоты ω₀ имеется узкий диапазон частот, в пределах которого концентрируется спектр АМ-колебания. Сиг­налы, спектр которых располагается в диапазоне частот, суще­ственно меньшем частоты несущего колебания, называются узко­полосными сигналами.

          Пример 4.1. На рис. 4.9 показаны прямоугольный радиоимпульс и его огибающая. Необходимо найти спектр радиоимпульса, имеющего дли­тельность τ_и и амплитуду U_m.

          Решение. Одиночный радиоимпульс описывается выражением u_AM = s(t)cos ω₀t_tгде  s(t)— огибающая радиоимпульса. Спектральную плотность огибающей радиоимпульса можно описать, используя выра­жение прямого преобразования Фурье (2.17):

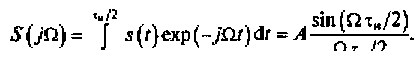
         Используя выражение (4.8), найдем спектральную плотность радио­импульса:

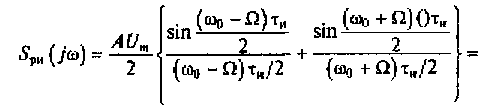
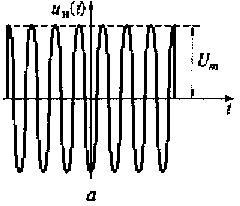
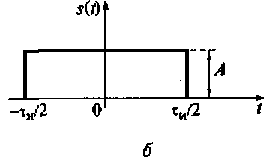
Рис. 4.9. Прямоугольный радиоимпульс (а) и его огибающая (б)

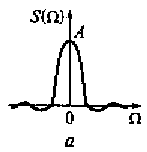
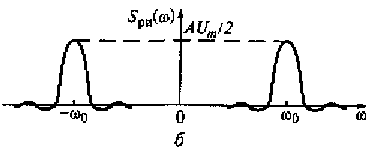
Рис. 4.10. Модули спектральной плотности огибающей (а) и радиоим­пульса (б)

=  AU_m {S[j(ω₀-Ω)]+S[j(ω₀+Ω)]}.

                                                         2

             Модули спектральной плотности огибающей S(Ω) и радиоимпульса S_ри(ω) приведены на рис. 4.10. Видно, что по форме они совпадают меж­ду собой. Однако модуль спектральной плотности огибающей располага­ется в районе нулевой частоты, а модули спектральной плотности ра­диоимпульса — в окрестности частот ω₀ и - ω₀.

4.5. Радиосигналы с угловой модуляцией

          В гармоническом колебании u(t) = U_mcos(ω₀t+φ₀) величина ψ = ω₀t+φ₀ называется мгновенной фазой. Круговая частота ω₀ и на­чальная фаза φ₀  в гармоническом колебании являются постоян­ными величинами. Однако, организуя изменения мгновенной фазы в соответствии с модулирующим сигналом, можно получить ко­лебания с угловой модуляцией. Различают два вида угловой модуля­ции — частотную и фазовую, В таких колебаниях амплитуда моду­лированного сигнала остается неизменной.

         Мгновенную фазу сигнала с угловой модуляцией можно запи­сать в виде

                                                              ψ(t)= ω₀t+ku(t)                                               (4.9)

где k — коэффициент пропорциональности; u(t) — модулирую­щий сигнал; ω₀ — частота высокочастотного несущего колебания.

         Сигналы, мгновенная фаза которых изменяется в соответствии с выражением (4.9), называются фазомодулированными сигналами:

                                        u_ФМ(t)= U_mcos [ω₀t+ku(t)]                                   (4.10)

На рис. 4.11 показаны модулирующий и фазомодулированный сигналы. Пусть модулирующий сигнал u(t) изменяется по гармо­ническому закону (см. рис. 4.11, а). С ростом амплитуды модулиру­ющего сигнала растет фаза несущего колебания, между начальной фазой которого (кривая 2 на рис. 4.11, б) и ФМ-сигналом (кри­вая 3 на рис. 4.11, 6) появляется дополнительный фазовый сдвиг ∆ψ. Максимальная величина дополнительного фазового сдвига про­порциональна максимальной амплитуде модулирующего сигнала.

При снижении амплитуды модулирующего сигнала ∆ψ также уменьшается. При равенстве нулю модулирующего сигнала u(t)=0 дополнительный фазовый сдвиг также равен нулю, т.е. ∆ψ=0. Та­ким образом, определив закон управления мгновенной фазой не­сущего колебания, можно также получить сигналы с угловой мо­дуляцией.

         Дифференциал от мгновенной фазы называется мгновенной частотой ω(t) сигнала с угловой модуляцией:

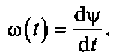                                     (4.11)

С учетом этого мгновенная фаза сигнала

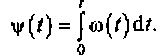                                                                     (4.12)

          При ЧМ мгновенная частота модулированного сигнала пред­ставляется в виде

                                                                 (4.13)

где u(t) — модулирующий сигнал; k — коэффициент пропорцио­нальности.

           Тогда в соответствии с выражениями (4.11) —(4.13) можно за­писать выражение, описывающее ЧМ-сигнал:

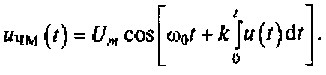 (4.14)

В выражении (4.14) величина k определяет диапазон изменения частоты несущего ко­лебания под действием модули­рующего сигнала. Максимальное изменение частоты достигается при максимальной амплитуде модулирующего сигнала и назы­вается девиацией частоты: ∆ω=k|U_уmax|.

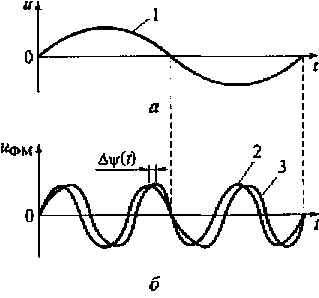
Рис. 4.11. Модулирующий (а) и фазомодулированный (б) сигналы

В общем виде ФМ- и ЧМ-колебания при непрерывных управ­ляющих сигналах не отличаются друг от друга. Однако эти сигна­лы имеют принципиальное отли­чие относительно управляющего воздействия модулирующего сиг­нала на параметры несущего колебания. У ФМ-колебания фазовый сдвиг между модулированным сигналом и исходным несущим колебанием пропорционален из­менению модулирующего сигналаu(t), а у ЧМ-колебания этот фазовый сдвиг пропорционален интегралу от модулирующего сиг­нала u(t).

4.6. Частотная модуляция

           Пусть тональный сигнал u(t)= U_у cosΩt модулирует по частоте высокочастотное гармоническое колебание u_н(t) = U_mcos(ω₀t+φ₀).   Тогда, согласно (4.13), мгновенную частоту ЧМ-колебания мож­но записать следующим образом:

(4.15)

где ∆ω=kU_у-девиация частоты.

           Взяв интеграл от формулы мгновенной частоты ЧМ-колебания (4.15), найдем закон изменения мгновенной фазы этого сигнала:

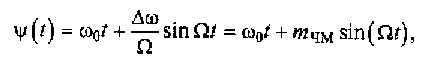                                                                 (4.16)

где m_чм =∆ω/Ω = kUy/Ω— индекс частотной модуляции.

               Индекс частотной модуляции m_чм характеризует девиацию мгно­венной фазы сигнала. Он может быть как существенно меньше единицы, так и превышать единицу. С учетом этого и рассмотрим спектр ЧМ-колебания, полученного при использованиитональ­ного модулирующего сигнала.

                При малом индексе m_чм (m_чм< 1) ЧМ-колебание во времен­ной области можно описать выражением

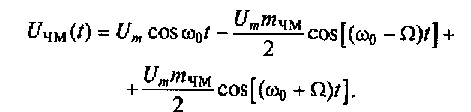 (4.17)

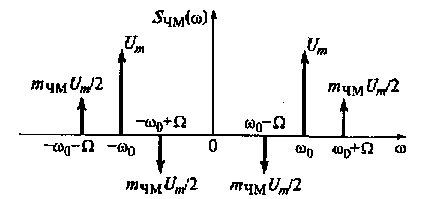
Рис. 4.12. Спектральная характеристика тонального ЧМ-колебания

с ма­лым индексом модуляции

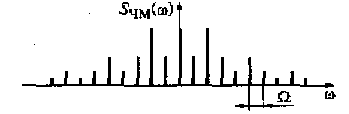
Рис. 4.13. Спектр ЧМ-колебания с большим индексом модуляции

              Полученное выражение по своей структуре соответствует вы­ражению, описывающему спектр АМ-колебания при тональной модуляции. Их отличие состоит лишь в том, что спектральная ха­рактеристика тонального ЧМ-колебания с малым индексом мо­дуляции, приведенная на рис. 4.12, в области частоты ω₀-Ω сдви­нута по фазе на 180⁰ — знак «минус» у второго слагаемого в выра­жении (4.17).

              Колебание с ЧМ при большом значении индекса модуляции m_чм представляет собой множество спектральных составляющих, частоты которых кратны частоте ω₀+kΩ, а амплитуды снижаются при увеличении k. На рис. 4.13 показан спектр ЧМ-колебания с большим индексом модуляции.