Линейные цепи с сосредоточенными параметрами. Линейные четырехполюсники. Колебательные контуры (5-7 главы учебника "Радиотехнические цепи и сигналы" под ред. К.Е.Румянцева), страница 16

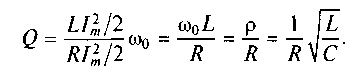
Рис. 7.4. Зависимость тока в контуре, имеющем потери, при R > 2р

              Отметим, что при Q > 0,5 в контуре устанавливается сво­бодный колебательный процесс (см. рис. 7.3). При Q < 0,5 ток в контуре изменяется по аперио­дическому закону (см. рис.7.4). На практике добротность реаль­ного контура определяется доб­ротностью индуктивной катушки и составляет величину 50...300, в связи с чем в контуре всегда будет присутствовать колебательный процесс при внесении в кон­тур энергии от внешнего источника. Величина, обратная добротно­сти, называется затуханием d= 1/Q.

7.3. Реальные колебательные контуры.

Понятия и определения

              Среди колебательных контуров различают последовательные и параллельные контуры.

             Последовательный колебательный контур представляет собой последовательное соединение индуктивной катушки L, конден­сатора С  и источника энергии e(t), в качестве которого выступает источник напряжения. На рис. 7.5 показана схема последователь­ного колебательного контура, а на рис. 7.6 приведены схемы па­раллельных контуров основного вида и с разделенными индук­тивностью и емкостью. Особенностью параллельных колебатель­ных контуров является то, что обе ветви контуров включены па­раллельно источнику энергии, в качестве которого используется источник тока.

             Каждый из пассивных элементов, входящих в колебательный контур, включает реактивное сопротивление, характеризующее емкость конденсатора или индуктивность катушки, и активное сопротивление, т.е. сопротивления потерь конденсатора и индук­тивной катушки.

            Резонансом колебательного контура называется явление, при котором реактивная составляющая комплексного входного сопро­тивления для последовательного контура и реактивная составля­ющая комплексной входной проводимости для параллельного кон­тура близки к нулю. Это приводит к тому, что при резонансе про­исходит резкий рост амплитуды колебательного процесса в кон­туре по сравнению с амплитудой входного воздействия. Для пос­ледовательного контура это означает, что действующие значения напряжения на емкости U_c и индуктивности U_Lравны между со­бой, но противоположны по фазе (U_c=|-U_L| ).

              Напряжение, падающее на сопротивлении потерь U_R,равно напряжению входного воздействия и совпадает по фазе с током входного воздействия. При этом U_c» U_Rи состояние контура называется ре­зонансом напряжений.

               В параллельном контуре при ре­зонансе действующие значения то­ков емкости I_c и индуктивности I_L. Равны между собой, но противо­положны по фазе I_L=|-I_c| , а входной ток

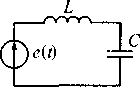
Рис. 7.5. Схема последовательного колебательного контура

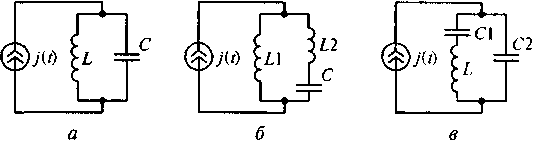
Рис. 7.6. Схемы параллельного контура основного вида (а) и

с разделенными индуктивностью (б) иемкостью (в)

равен току I_R, протекающему через сопротивление потерь и совпадает по фазе с напряжением на внешних зажимах контура. При этом I_L»I_R  и   |I_c|»I_R. Подобное состояние контура называется резонансом токов.

7.4. Последовательный колебательный контур

               На рис. 7.7 приведена эквивалентная схема последовательного колебательного контура, которая включает индуктивность Lка­тушки, емкость С конденсатора и сопротивление потерь R, равное сумме сопротивлений потерь индуктивной катушки R_Lи кон­денсатора R_c,т. е. R = R_L + R_c.

              Питается контур от генератора, напряжение которого изменя­ется по гармоническому закону e(t) = u₁(t) = U_mcos(ωt + ψ_и). Гене­ратор напряжения может иметь внутреннее сопротивление R_i ко­торое также суммируется с сопротивлениями потерь контура.

               Наличие сопротивления потерь приводит к затуханию свобод­ных колебаний в контуре (амплитуда колебаний от периода к пе­риоду снижается) из-за рассеивания энергии на сопротивление потерь R. Введение в контур генератора напряжения e(t) позволя­ет компенсировать потери энергии в контуре и обеспечить незату­хающий колебательный процесс с постоянной амплитудой.

               Выходное напряжение контура u₂(t) может сниматься как емкости (см. рис. 7.7), так и с индуктивности, что требует под­ключения к выходным зажимам контура сопротивления нагрузки  R_н, характеризующего, например, входное сопротивление после­дующего усилительного каскада.

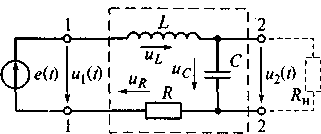
Рис. 7.7. Эквивалентная схема по­следовательного колебательного контура

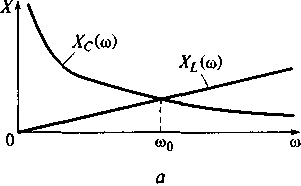
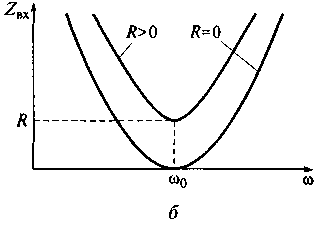
               При резонансе в контуре реактивная составляющая Х_вх =ω₀L-1/(ω₀С) входного сопротивления Z_вx контура равна нулю. Отсю­да можно найти частоту свободных колебаний (резонансную частоту) в контуре ω₀ = 1/√(LC) .

               На резонансной частоте реактивные сопротивления индуктив­ности Z_L(ω₀) =ω₀L= √(L/С) = р  и ёмкости Z_c(ω₀) = 1/(ω₀ С) =√(L/С) = р контура равны между собой и равны характеристи­ческому сопротивлению контура.

                Комплексное входное сопротивление последовательного кон­тура  Z_вх(jω)       представляет сопротивление контура относительно его входных зажимов 1 — 1 , к которым подключен генератор на­пряжения внешнего воздействия e(t) с комплексной амплитудой Ů _т = U_m ехр(jψ_и) . В соответствии с законом Ома в комплексной форме Z_вх(jω)       равно частному от деления комплексной амплиту­ды входного напряжения на комплексную амплитуду входного тока либо частному от деления комплексного действующего значения напряжения на комплексное действующее значение тока. Поэтому

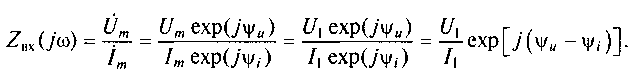
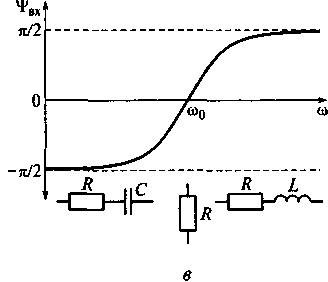
              В общем случае входное напряжение и входной ток не совпада­ют по фазе. Поэтому входное сопротивление контура является комплексным:

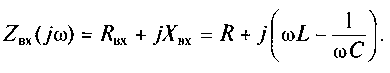                                                                          (7.8)

              В показательной форме входное сопротивление контура имеет  вид

где

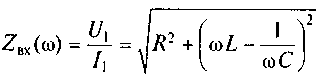
полное входное сопротивление контура; ψ_вх= ψ_и - ψ_i= arctg ((ωL-1/(ωC))/R)  — фазовый сдвиг между напряжением и током на входных зажимах контура.

              Зависимости реактивных сопротивлений индуктивности и ем­кости, модуля комплексного входного сопротивления и аргумен­та последовательного контура от частоты представлены на рис. 7.8. Видно, что модуль входного сопротивления и аргумент контура сильно зависят от частоты.