Линейные цепи с сосредоточенными параметрами. Линейные четырехполюсники. Колебательные контуры (5-7 главы учебника "Радиотехнические цепи и сигналы" под ред. К.Е.Румянцева), страница 12

Ė_r-İ₁ Z_r =A₁₁Ů₂+(A₁₂ /Z_H2)Ů₂;

                                                          İ₁=A_2lŮ₂+(A₂₂/Z_H2)Ů₂.                    

           Из полученной системы, разделив первое уравнение на вто­рое, найдем значение рабочего входного сопротивления

                          Z_вх.р(jω)=Ė_r/İ₁=Z_r + (A₁₁Z_H2+A₁₂)/( A₂₁Z_H2+A₂₂).                      (6.7)

            При Z_H2 = 0 рабочее входное сопротивление преобразуется к виду

                                                     Z_вх.р (jω) = Z_r+ A₁₂/A₂₂.(6.8)

            При Z_H2 →∞ да рабочее входное сопротивление сводится к иному виду

                                                                    Z_вх.р (jω) = Z_r+ A₁₁/A₂₂.(6.9)

           Согласно рис. 6.7 имеем Ё_r = Ů₁ + İ₁ Z_r и Ů₂ = İ´₂Z_H2. Из полу­ченных равенств находим формулу для расчета рабочего коэффи­циента передачи напряжения анализируемой цепи:

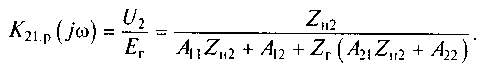                                                      (6.10)

             Из (6.10) видно, что K₂₁._p (jω) = 0 при Z _H2 = 0, а при Z _H2 →∞ рабочий коэффициент передачи напряжения цепи принимает вид

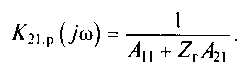                                                                                                    (6.11)

             Анализируя формулы (6.7) —(6.11), можно сделать следующие выводы:

             изменяя величину Z _H2, можно выбрать требуемые рабочие вход­ное сопротивление и коэффициент передачи напряжения четы­рехполюсника в соответствии с его первичными параметрами;

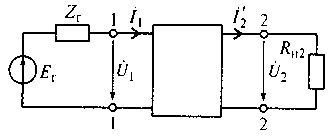
Рис. 6.7. Электрическая цепь для оп­ределения

рабочих характеристик четырехполюсника

            рабочее входное сопротивление и рабочий коэффициент пе­редачи напряжения цепи сильно зависят от внутреннего сопро­тивления источника входного напряжения: рабочее входное со­противление с ростом Z_r растет, а рабочий коэффициент переда­чи напряжения уменьшается.

            При анализе радиотехнических цепей широко используют по­нятие характеристическое сопротивление, под которым понимают сопротивления со стороны зажимов 1 — 1 или 2 — 2 четырехполюс­ника, равные по величине соответствующим сопротивлениям на­грузки, т.е. Z_cl = Z_Hl, Z_c2 = Z_H2, где Z_cl и Z_c2 — характеристические сопротивления со стороны зажимов 1 — 1 или 2 — 2 соответственно.

            На рис. 6.8 приведена схема цепи каскадного соединения двух четырехполюсников А и В. В данном случае под согласованным соединением этих четырехполюсников понимается следующее. Некоторое характеристическое сопротивление Z_c2B со стороны зажимов 2 — 2 четырехполюсника В равно Z_H2, т. е. Z_c2B = Z_H2. Соот­ветственно Z_c2A = Z_c1B. При включении сопротивления нагрузки со стороны зажимов 1 — 1 должны выполняться условия Z_c1A = Z_H1 и Z_c1B = Z_c2A. В этом случае соединение двух четырехполюсников в единую цепь не приводит к нарушению баланса токов и напряже­ний в узлах их соединения. Характеристические сопротивления такого четырехполюсника

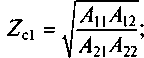
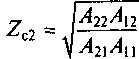                                                                        (6.12)

определяются только его первичными параметрами.

             Пример 6.4. Используя данные примера 6.2 относительно A-параметров четырехполюсника, необходимо найти характеристические сопро­тивления заданного четырехполюсника при согласованной нагрузке относительно зажимов 2 — 2 и 1 — 1.

              Решение. A-параметры четырехполюсника (см. рис. 6.2, а) имеют вид

А₁₁ = 1 + Z₁ /Z₂; A₁₂ = Z₁ ; A₂₁ = 1/Z₂; A₂₂ = 1. Для нахождения характери­стических сопротивлений Z_cl и Z_c2 используем выражения (6.12). Тогда

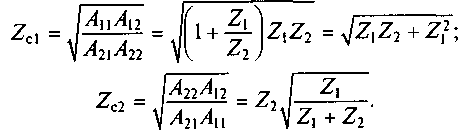
           Важным параметром четырехполюсников является характери­стическая постоянная передачи:

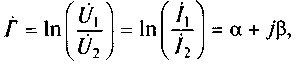
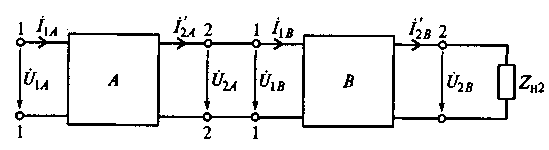
Рис. 6.8. Схема цепи каскадного соединения двух четырехполюсников

где Ů₁ и Ů₂ — комплексные амплитуды напряжений, а İ₁ и İ₂ — комплексные амплитуды токов на входных и выходных зажимах четырехполюсника.

          Действительная часть α характеристической постоянной пере­дачи называется коэффициентом ослабления сигнала и характери­зует изменение амплитуды сигнала. Мнимая часть β комплексного числа Г называется коэффициентом фазы и характеризует измене­ние фазы сигнала при передаче его от входных к выходным зажи­мам четырехполюсника.

          Комплексные амплитуды входного и выходного напряжений имеют вид:

Ů₁= U₁ ехр(jψ_u1); Ů₂ = U₂ехр(jψ_u2). В этом случае ко­эффициенты α и β будут определяться выражениями:

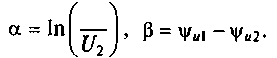
Коэффициент ослабления α на практике выражается в децибелах:

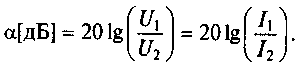
6.5. Составные четырехполюсники

           Под составным четырехполюсником понимают четырехполюс­ник, который может быть представлен множеством более простых четырехполюсников, соответствующим образом соединенных меж­ду собой. Таким образом, для упрощения анализа радиотехничес­ких цепей сложную цепь можно разбить на множество простых четырехполюсников. К числу наиболее часто используемых соеди­нений относят каскадное, параллельное и последовательное со­единения.

           Для выделенных четырехполюсников можно определить пер­вичные параметры (см. табл. 6.1). Учитывая варианты соединения четырехполюсников, можно получить первичные параметры со­ставного четырехполюсника и вычислить различные характерис­тики, например комплексные частотные, применительно к этому четырехполюснику.

           При разбиении составного четырехполюсника необходимо соблюдать баланс токов и на­пряжений относительно узлов соединения простых четырехпо­люсников.

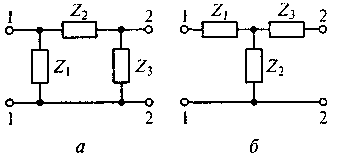
Рис. 6.9. Схемы электрических це­пей П-образного (а)

и Т-образно­го (б) четырехполюсников

Пример 6.5. На рис. 6.9 приведе­ны схемы электрических цепей П-образного и Т-образного четырех­полюсников. Необходимо предста­вить оба четырехполюсника в виде составных четырехполюсников.

            Решение. П-образный и Т-образный четырехполюсники пред­ставим в виде двух последовательно соединенных четырехполюсников, соответственно показанных на рис. 6.10, аи рис. 6.10, б. Для соблюде­ния баланса токов и напряжений в узлах их соединения в первом слу­чае (П-образный четырехполюсник) сопротивление Z₂разобьем на два каждое величиной Z₂/2, а во втором Т-образный четырехполюсник — на 2Z₂.