Электротехника \ Радиотехнические цепи и сигналы

Линейные цепи с сосредоточенными параметрами. Линейные четырехполюсники. Колебательные контуры (5-7 главы учебника "Радиотехнические цепи и сигналы" под ред. К.Е.Румянцева), страница 10

ΔA = A11A22-Al2A21.

           Поскольку в четырехполюсник могут входить такие элементы, как сопротивления, емкости и индуктивности, то первичные параметры четырехполюсников в общем виде являются комплекс­ными величинами. Параметры четырехполюсников могут иметь размерность, например, сопротивления Z11 =Ů1/İ1 или прово­димости H22 = İ2/ Ů2 , а также быть безразмерными, например, H21 = İ2/ İ1 или A11=Ů1/ Ů2.

Таблиц а   6.1

Системы уравнений, описывающие четырехполюсники

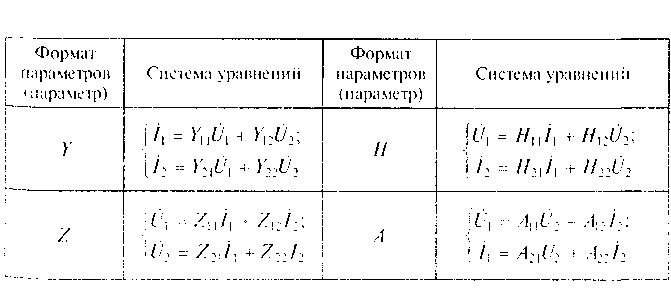
           Для определения первичных параметров четырехполюсника используют метод «короткого замыкания — холостого хода» («кз —хх»). Его суть заключается в следующем. Ни одна из систем уравнений, приведенных в табл. 6.1, однозначного решения не имеет, так как число неизвестных в 2 раза больше числа уравне­ний в каждой системе. Для решения данной задачи принимают равными нулю напряжения на зажимах 1 — 1 или 2 — 2 (короткое замыкание) либо принимают равными нулю токи, протекаю­щие через зажимы 1 или 2 (холостой ход). В этом случае система уравнений сводится к двум уравнениям с двумя неизвестными и, соответственно, параметры четырехполюсника определяются однозначно.

Таблица   6.2

Соотношения первичных параметров четырехполюсника

Параметр

Параметр

Y

Z

H

A

Y

-

Z22/ΔZ;

-Z12/ΔZ;

-Z21/ΔZ;

Z11/ΔZ

1/H11;

-H12/H11;

H21/H11;

ΔH/H11

A22/A12;

-ΔA/A12;

-1/A12;

A11/A12

Z

Y22/ΔY;

-12/ΔY;

 -Y21/ΔY;

Y11/ΔY

-

ΔH/H22;

-H12/H22;

-H21/H22;

1/H22

A22/A21;

ΔA/A21;

1/A21;

A22/A21

H

1/ΔY;

 -Y12/ΔY;

 -Y21/ΔY;

ΔY/Y11

ΔZ/Z22;

Z12/Z22;

-Z21/Z22;

1/Z22

-

A12/A22;

ΔA/A22;

-1/A22;

A21/A22

A

-Y22/Y21;

-1Y12/ Y21;

 -ΔY/Y21;

 -Y11/ Y21

Z11/Z21;

ΔZ/Z21;

1/Z21;

Z22/Z21

-ΔH/H21;

-H11/H21;

H22/H21;

-1/H21

-

Пример 6.1. Необходимо определить Z-параметры четырехполюсни­ка, представленного на рис. 6.2, а.

          Решение. Для нахождения Z-параметров четырехполюсника исполь­зуем систему уравнений:

 


   Ů1=Z11İ1+Z12İ2;

                                                       Ů2 = Z21İ1 + Z22 İ2.

            Принимаем, что выходной ток четырехполюсника İ2 равен нулю (хо­лостой ход на зажимах 2 — 2). Тогда Ů1=Z11İ1, и  Ů2 =Z2Iİ1. Откуда Z11=Ů1/İ1, Z21=Ů2/İ1.

            Так как напряжение на входе четырехполюсника Ů1, задано, то входной ток можно определить по формуле İ1 = Ů1 /(Z1 + Z2) . Откуда Z11 = Z1 + Z2.

            При İ2=0 напряжение на вторых зажимах четырехполюсника мож­но представить в виде Ů2 = Ů1 Z2/(Z1 + Z2) . Тогда

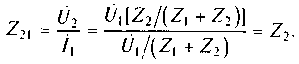
            Реализуем холостой ход на зажимах 1 — 1 четырехполюсника. В ре­зультате этого имеем İ1 = 0 , Ů1= Z12İ2  и Ů2 = Z22İ2. Откуда ZI2 = Ů1/İ2 и Z22=Ů2/İ2.

            Пусть известно напряжение Ů2 . При этом Ů1 = Ů2 и İ2 = Ů2 /Z2 . От­куда ZI2 = Ů1 / İ2 = Z2 и Z22 = Ů2 / İ2 = Z2.

Пример 6.2. Известны Z-параметры четырехполюсника, показанного на рис. 6.2, a: Z11 = Z1 + Z2, Z12= Z2I = Z22 = Z2. Необходимо определить A-пaраметры четырехполюсника.

             Решение. Воспользуемся соотношениями, приведенными в табл. 6.2:

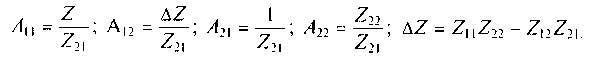
             Подставляя исходные данные в эти выражения, находим:

ΔZ= (Z1 + Z2)Z2 - Z2Z2 = Z2(Z1 + Z2 - Z2) = Z1 Z2;

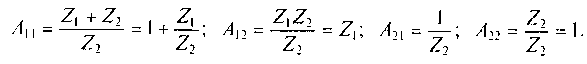
             Метод «кз — хх» позволяет определить параметры четырехполюс­ника как расчетным путем, зная внутреннее содержание четы­рехполюсника, так и экспериментально, если внутреннее содер­жание четырехполюсника неизвестно.

Для экспериментальной оценки параметров четырехполюсника необходимо произвести измерения необходимых токов и напряже­ний при выполнении условия «кз» или «хх» на соответствующих зажимах четырехполюсника, а затем использовать одну из систем уравнений (см. табл. 6.1) с требуемыми первичными параметрами для их определения.

            Зная первичные параметры четырехполюсника, можно опре­делить входные и выходные параметры четырехполюсника, а так­же его передаточные характеристики для анализа четырехполюс­ника в частотной и временной областях.

6.2. Модели неавтономных четырехполюсников

              Любой неавтономный четырехполюсник может быть представ­лен различными по структуре и форматам параметров четырехпо­люсниками. При этом число элементов в любой модели не должно превышать четырех. На рис. 6.3 показаны Т-образная и П -образная модели четырехполюсников, наиболее часто используемых в ра­диотехнике.

              Для четырехполюсника, показанного на рис. 6.3, а, Z-параметры имеют вид

Z11 = Z1 + Z2; Z12 = Z2; Z21 = Z2 + Z4; Z22 = Z2 + Z3.

             Это позволяет установить параметры Т-образной модели:

Z1 = Z11 - Z12; Z2 = ZI2; Z3= Z22 - Z 12; Z4 = Z21 - ZI2.

               Для четырехполюсника (см. рис. 6.3, б) Y-параметры имеют вид

Y11=Y1+Y2; Y12= -Y2; Y21=Y4-Y3; Y22=Y2+Y3.

                Тогда можно найти зависимость параметров элементов П-образной модели от параметров четырехполюсника:

                Таким образом, зная первичные параметры четырехполюсни­ка относительно его внешних зажимов, полученные, например, экспериментальным путем, можно построить различные модели четырехполюсника, которые пригодны для анализа более слож­ных радиотехнических цепей.

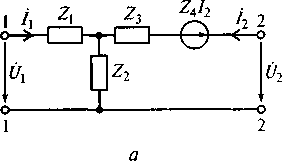
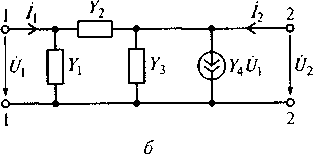
Рис. 6.3. Т-образная (а) и П-образная (б) модели четырехполюсников

6.3. Комплексные частотные характеристики линейных цепей

             Способность электрической цепи передать сигнал от пары за­жимов, к которой подключен источник энергии, к паре зажи­мов, к которой подключен нагрузочный элемент, характеризует­ся комплексной частотной характеристикой (КЧХ) цепи.

             Пусть зажимы 1 — 1 четырехполюсника (см. рис. 6.1, а) являются входными и к ним подключен источник энергии. Зажимы 2 —2 — выходные и к ним может быть подключено сопротивление на­грузки. Пусть в качестве входного воздействия выступает сигнал X(jω), а выходного отклика — сигнал S(jω). Тогда под КЧХ, обо­значаемой H(jω), понимают отношение отклика цепи к входно­му воздействию, т.е. H(jω) = S(jω)/X(jω) =HД(ω) + jHМН(ω), где HД(ω)  и HМН(ω) — действительная и мнимая части комплексного числа.

Скачать файл