Колебательным контуром называют замкнутую цепь, состоящую из реактивных элементов различного типа, т.е. из индуктивных катушек и конденсаторов. В простейшем случае в колебательный контур входят одна индуктивная катушка и один конденсатор.
На рис. 7.1 показаны электрическая цепь, не имеющая потерь, и колебательные процессы, происходящие в ней.
Для того чтобы понять процессы, происходящие в колебательном контуре, рассмотрим свободные колебания в идеальном колебательном контуре (см. рис. 7.1, а), в котором сопротивления потерь индуктивной катушки и конденсатора равны нулю (RL= 0, Rc= 0). В этом случае потери энергии в контуре отсутствуют.
Чтобы зарядить конденсатор до напряжения источника Еп, замкнем переключатель S в положение 1. В результате этого включения верхняя обкладка конденсатора получит положительный заряд, а нижняя — отрицательный. В конденсаторе накопится энергия Wc =ЕП2 С/2, которая определит ЭДС емкости ес.
Зарядив конденсатор в момент времени t=0 (см. рис. 7.1, б), переведем переключатель S в положение 2. В этом случае конденсатор начнет выступать в роли вторичного источника энергии. Его ЭДС ес будет приложена к индуктивной катушке, выступающей в роли нагрузки. В цепи должно выполняться равенство мгновенных значений напряжений uc(t) = uL(t) и токов ic(t) = iL(t) = i(t). Так как напряжения на конденсаторе и индуктивности изменяются по законам uc(t) = Еп -(1/С) ∫0t i(t)dt и , uL(t) =L (di(t)/dt), то для идеализированного контура можно записать уравнение
Еп =(1/С) ∫0t i(t)dt + L (di(t)/dt)(7.1)
Решением уравнения является функция
i(t) = Imsin(ω0t), (7.2)
где Im = En √(C/L) — амплитуда колебаний тока; ω0 = 1/√(CL) —круговая частота свободных колебаний в контуре.
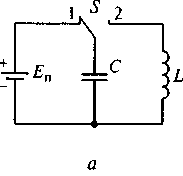
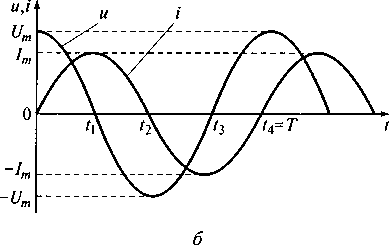
Рис. 7.1. Электрическая цепь, не имеющая потерь (а),
и колебательные процессы, происходящие в ней (б)
Рост тока в цепи будет продолжаться от 0 до Im пока ЭДС емкости ес не станет равной нулю (момент времени t = t1, на рис. 7.1, б). В этот момент индуктивная катушка накопит максимальную энергию WL = LIm2/2, а энергия конденсатора будет равна нулю. Энергия катушки при t=t1равна энергии конденсатора при t = 0.
Несмотря на то что в момент t = t1напряжение ис = 0, ток в цепи не может исчезнуть мгновенно, так как уменьшение тока сопровождается возникновением ЭДС самоиндукции индуктивной катушки eL. Эта ЭДС поддерживает протекание тока в том же направлении, что и на интервале времени [0, t1], заряжая нижнюю обкладку конденсатора положительно, а верхнюю отрицательно. Таким образом, в интервале времени [t1,t2] вторичным источником энергии выступает индуктивная катушка, а потребителем — конденсатор. Ток, протекающий в конденсаторе и индуктивной катушке, будет один и тот же (iL = iс). При этом напряжение на конденсаторе изменяется во времени по закону
![]() (7.3)
(7.3)
где Um = Im √(L/C) = Еп — амплитуда колебаний напряжения.
В интервале времени [t1,t2] ток в цепи, определенный энергией индуктивной катушки, будет уменьшаться. Это приведет к накоплению энергии в конденсаторе. При
iL = 0 в момент t = t2 напряжение uс достигнет величины -Um = -En. Энергия в емкости Wc при t = t2 будет равна энергии индуктивной катушки при t = t1.
В интервалах времени [t2, t3] и [t3,t4 ] процессы, протекающие в цепи, будут те же, что и в интервалах [0,t1] и [t1,t2] соответственно. Отличие будет только в том, что напряжение на контуре и ток в цепи будут иметь противоположные направления.
Через период повторения переходного процесса в контуре Т = 2π/ω0 состояние контура возвращается в исходное положение, соответствующее моменту t= 0. При t> Т процесс в цепи продолжается бесконечно долго, поскольку в цепи потери энергии отсутствуют, а наблюдается только перенос энергии от конденсатора к индуктивной катушке и обратно.
В соответствии с формулами (7.2) и (7.3) свободные колебания в идеальном контуре описываются гармоническими функциями и зависят от круговой частоты свободных колебаний в контуре ω0 = 1/√(CL).
В идеальном контуре потери энергии отсутствуют. В результате этого происходит полное преобразование энергии одного вида в другой (электрической энергии в магнитную энергию и наоборот). Так как максимальные значения электрической и магнитной энергий контура равны между собой Um2C/2=Im2L/2, то Um/Im = √(L/C) = р. В этом уравнении величина
![]() (7.4)
(7.4)
определяет отношение амплитуд напряжения и тока и называется характеристическим сопротивлением контура.
Поскольку частота свободных колебаний в контуре ω0 = 1/√(CL) определяется параметрами реактивных элементов (индуктивностью катушки Lи емкостью конденсатора С), то изменения тока (7.2) и напряжения (7.3) в контуре зависят только от параметров реактивных элементов. Частота свободных колебаний в контуре называется резонансной частотой контура.
Полные сопротивления индуктивности и емкости определяются по формулам:
ХL = ωL и Хс= 1/(ωС). На резонансной частоте контура находим:
XL=ω0L=L/√(LC)=√(L/C)=p; Xc=1/(ω0C)=√(LC)/C=√(L/C)=p.
Таким образом, на резонансной частоте контура полные сопротивления индуктивности и емкости равны между собой ω0L=1/(ω0C) и равны характеристическому сопротивлению контура (7.4).
Процесс изменения тока и напряжения в контуре, не имеющем потерь, продолжается бесконечно долго. В выражениях (7.2) и (7.3), описывающих изменение тока и напряжения в идеальном контуре, значения функций синус и косинус повторяются через период Т =2π/ω0. Тогда период изменения тока и напряжения в контуре может быть рассчитан по формуле Т = 2π√(LC).
Длина волны колебаний в контуре определяется выражением
λ0=cT=c2π√(LC)=3·108·2π√(LC)=1,88·109√(LC),
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.