Качество индуктивной катушки оценивается ее добротностью ql= tgψ = ωL/R, которая характеризует доли напряжений, падающие на индуктивности и сопротивлении потерь. Чем выше сопротивление потерь, тем меньше добротность индуктивной катушки
QL=UL/UR=(√2IωL)/(√2IR)=(ωI)/R.
С ростом частоты о потери в индуктивной катушке растут и ее добротность снижается. Для реальных индуктивных катушек добротность лежит в диапазоне QL= 50...200.
При рассмотрении добротности конденсатора учтем, что его паразитная индуктивность имеет малую величину. Тогда модель конденсатора представляет цепь из последовательно соединенных сопротивления потерь Rи емкости С (рис. 5.17, а).
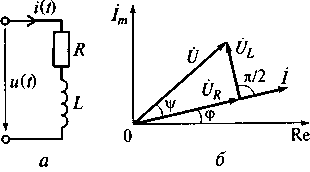
Рис. 5.16. Модель индуктивной катушки (а) и диаграмма распределения комплексных токов и напряжений в ней (б)
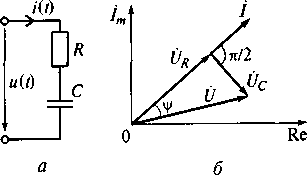
Рис. 5.17. Модель конденсатора (а) и диаграмма распределения напряжений
на элементах цепи (б)
Пусть к этой цепи приложено напряжение, изменяющееся по гармоническому закону и(t) = √2Ucos(ωt + φ). Тогда комплексная амплитуда напряжения на входных зажимах цепи будет иметь вид (рис. 5.17, б) Ů = √2 U ехр(jφ). Соответственно, амплитуда комплексного тока равна
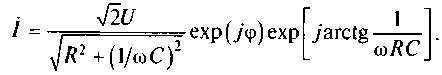
Из данного выражения видно, что ток в цепи опережает напряжение на угол ψ = arctg(l/ωCR). При отсутствии потерь (R = 0) фазовый сдвиг составляет ψ = arctg(∞) = π/2.
В этом случае потери энергии в конденсаторе отсутствуют. При наличии потерь (R > 0) имеем ψ < π/2 (см. рис. 5.17, б). Это говорит о потерях энергии в конденсаторе, которые характеризуются его добротностью Qc = = tgψ= 1/(ωRC).
Добротность конденсатора отражает доли напряжений, которые падают на емкость и сопротивление потерь: Qc = Uc/UR=1/( ωRC).
Величина, обратная добротности, называется тангенсом угла диэлектрических потерь конденсатора: tgβ = 1/Q = ωRC.
Сопротивление потерь конденсатора с ростом частоты возрастает, а его добротность, наоборот, снижается. Для конденсаторов в рабочем диапазоне частот добротность, как правило, составляет величину Qc> 500.
ГЛАВА 6 ЛИНЕЙНЫЕ ЧЕТЫРЕХПОЛЮСНИКИ
6.1. Линейные четырехполюсники и их первичные параметры
Четырехполюсником называется электрическая цепь любой сложности, имеющая две пары внешних зажимов (полюсов). На рис. 6.1 показаны схемы четырехполюсника и биполярного транзистора с общим эмиттером. К одной из пар зажимов четырехполюсника подключается источник энергии внешнего воздействия, а ко второй — нагрузочный элемент.
В виде четырехполюсника можно представить как отдельные Радиокомпоненты, например биполярные (см. рис. 6.1, б) и полевые транзисторы, трансформаторы и электровакуумные приборы, так и электрические схемы, включающие множество соединенных между собой радиокомпонентов различных типов, например усилителей.
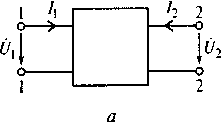
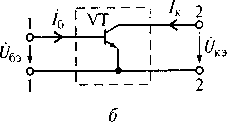
Рис. 6.1. Схемы четырехполюсника (а) и биполярного транзистора
с общим эмиттером (б)
Особенность представления электрических цепей в виде четырехполюсников заключается в соблюдении следующих двух положений.
1. При анализе сложных электронных цепей, включающих четырехполюсники, можно не рассматривать внутреннее содержание четырехполюсников, а оперировать их параметрами, которые приводятся к внешним выводам четырехполюсника. Это позволяет существенно сократить объем вычислений.
2. Четырехполюсник относительно внешних зажимов можно описать рядом характеристик, позволяющих анализировать прохождение сигналов от входных зажимов четырехполюсника к выходным в частотной и временной областях, не рассматривая внутреннее содержание четырехполюсника.
Пара зажимов четырехполюсника, к которой подключается источник энергии внешнего воздействия (источник напряжения или тока), называется входной. Пара зажимов четырехполюсника, с которой на нагрузочном элементе выделяется выходной сигнал (напряжение или ток), называется выходной. Четырехполюсник называется симметричным, если смена местами входных и выходных зажимов не приводит к изменению напряжений и токов на этих парах зажимов.
Четырехполюсники делят на три типа:
пассивные, которые не содержат в себе источников энергии;
активные, которые содержат в себе неуправляемые источники энергии;
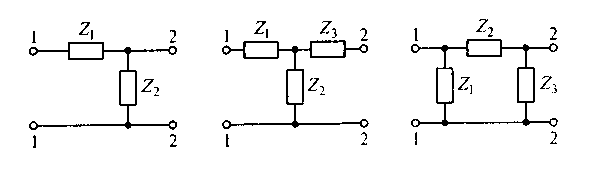
абв
Рис. 6.2. Варианты структурного построения четырехполюсников: а — Г-образный;
б — Т-образный: в — П-образный
неавтономные, содержащие в себе управляемые источники энергии, ток или напряжение которых зависят от токов или напряжений какой-либо ветви четырехполюсника.
На рис. 6.2 представлены варианты четырехполюсников с Г-образной, Т-образной и П-образной структурами.
Любой из четырехполюсников может быть описан системой из двух уравнений, которые объединяют в себе входное Ů1 и выходное Ů2 напряжения, входной İ1, и выходной İ2 токи и первичные параметры, как правило, комплексные. В основном варианте (см. рис. 6.1, а) принимается, что входной и выходной токи втекают в четырехполюсник. Однако возможен вариант, когда, например, входной ток втекает, а выходной ток вытекает из четырехполюсника либо входной ток вытекает, а выходной ток втекает в четырехполюсник.
С учетом различных комбинаций токов и напряжений на внешних зажимах четырехполюсника можно записать шесть различных систем уравнений, описывающих четырехполюсник. Рассмотрим системы уравнений, наиболее часто используемые при анализе радиотехнических устройств (табл. 6.1).
Параметры Y, Z, H и А, входящие в системы уравнений, называются первичными параметрами четырехполюсника. Они характеризуют тот или иной параметр четырехполюсника относительно внешних зажимов 1 — 1 (X11), 2 — 2 (Х22), 1—2 (Х12) и 2—1 (Х21). В системе уравнений относительно A-параметров выполняется условие İ2´= -İ2 . Так как в системы уравнений входят одни и те же токи и напряжения, то первичные параметры четырехполюсника Y, Z, Hи А связаны между собой очевидными соотношениями (табл. 6.2), в которых ΔZ = Z11Z22- Z12Z21, ΔY= Y11 Y22 - Y 12Y21 , ΔH = H11H22 -H12 H21 и
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.