6. При увеличении индуктивности контура в несколько раз, уменьшении во столько же раз емкости контура и сохранении сопротивления потерь без изменений добротность контура возрастает и пропорционально ей возрастает коэффициент передачи напряжения на резонансной частоте ш0, а кривая, описывающая АЧХ коэффициента передачи напряжения, обостряется (кривая 3 на рис. 7.10).
7.5. Избирательность последовательного колебательного
контура
На рис. 7.11 показаны спектры сигналов различных радиостанций, АЧХ идеального и реального контуров, спектральные составляющие на выходе контура.
Пусть имеется частотный диапазон, в котором работает ряд радиостанций (см. рис. 7.11, а), каждая из которых в этом диапазоне имеет свою частоту несущего колебания (ωрА, ωрВ, ...), а спектральные составляющие всех радиостанций имеют одинаковые амплитуды. Необходимо выделить во входных цепях радиоприемника спектральные составляющие сигнала, которые соответствуют одной радиостанции. Решить эту задачу можно с использованием колебательных контуров, являющихся избирательными устройствами. Под избирательностью электрической цепи понимают ее способность выделять колебания, соответствующие отдельным частотам, из множества колебаний с различными частотами.
Оценку избирательных свойств колебательного контура проведем, приняв во внимание то, что полоса частот, в которой работает одна радиостанция, во много раз меньше частоты несущего колебания сор. В этом случае отношение резонансной частоты контура со0 к частоте несущего колебания со можно считать равным единице. Используя понятие обобщенной расстройки (7.9), представим АЧХ коэффициента передачи напряжения в последовательном контуре в виде
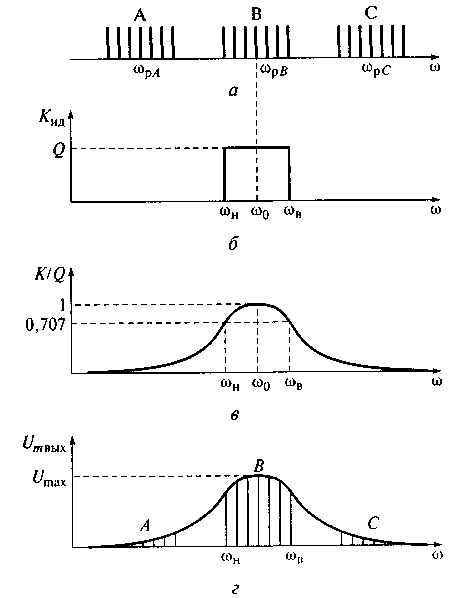
Рис. 7.11. Спектры сигналов различных радиостанций (а). АЧХ идеального (б) и реального (в) контуров, спектральные составляющие на выходе
реального контура (г)
![]()
На выходе избирательной системы можно найти амплитуды спектральных составляющих сигнала, умножив амплитуду каждой спектральной составляющей на входе контура на коэффициент передачи напряжения, определенный для той же частоты, что и для частоты входной спектральной составляющей.
Для неискаженной передачи сигналов АЧХ коэффициента передачи должна быть прямоугольной (см. рис. 7.11, б), т.е. в диапазоне частот ωн≤ω≤ωв коэффициент передачи должен быть равен Q, а вне этого диапазона — нулю (ωн и ωв — нижняя и верхняя частоты среза спектра сигнала избирательной системой). В этом случае амплитуды всех выходных спектральных составляющих в выделенном частотном диапазоне не подвергаются искажениям.
В реальных избирательных системах, построенных на базе колебательных контуров, АЧХ коэффициента передачи напряжения далека от идеальной (см. рис. 7.11, в). Это приводит к тому, что на выходе контура помимо спектральных составляющих требуемого частотного диапазона появляются и спектральные составляющие других частотных диапазонов. При этом амплитуды всех спектральных составляющих будут иметь разную величину, уменьшаясь при удалении частот вправо или влево от резонансной частоты ω 0 контура (см. рис. 7.11, г). Это приводит к частотным искажениям сигнала.
Количественно частотные искажения оценивают полосой пропускания контура Δω nр, равной разности частот, в пределах которой модуль коэффициента передачи напряжения уменьшается не более определенной величины. Обычно полосу пропускания оценивают на уровне 1/√2 = 0,707 максимального значения АЧХ коэффициента передачи. Это соответствует тому, что мощность сигнала на краях полосы пропускания контура снижается не более чем в 2 раза по сравнению с мощностью сигнала на резонансной частоте.
Оценим полосу пропускания контура на уровне 0,707. Значения обобщенной расстройки ξгр на границах полосы пропускания ω = ωн или ω =ωв контура соответственно равны -1 и +1. Используя выражение для обобщенной расстройки (7.9), на границах полосы пропускания контура можно записать
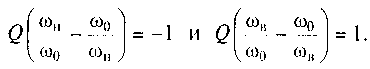
Отсюда находим нижнюю ωн и верхнюю ωв граничные частоты:
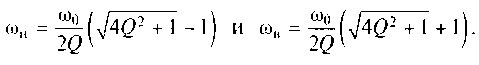
С учетом этого полоса пропускания последовательного контура по уровню 0,707 представляется в виде Δω= ωв- ωн = ω0/Q.
Анализ, проведенный относительно коэффициента передачи напряжения и избирательности последовательного колебательного контура, ориентирован на то, что добротность контура определяется только параметрами элементов контура. Однако генератор входного напряжения имеет свое внутреннее сопротивление Ri, которое оказывает влияние на добротность контура. Кроме того, при съеме выходного напряжения с индуктивной катушки или конденсатора входное сопротивление последующего каскада выступает в роли нагрузочного сопротивления относительно выходных зажимов колебательного контура. Это также оказывает влияние на добротность контура. Например, параллельно емкости, входящей в последовательный колебательный контур, включено сопротивление нагрузки RHl, а параллельно индуктивности RH2.
Таким образом, наличие внутреннего сопротивления генератора напряжения Riи нагрузочного сопротивления RH приводит к снижению эквивалентной добротности последовательного контура. Это, в свою очередь, делает АЧХ контура более пологой, коэффициент передачи напряжения на резонансной частоте снижается, а избирательные свойства контура ухудшаются.
Последовательные контуры находят широкое применение в радиоэлектронных устройствах, например в качестве избирательных цепей приемников или цепей, предназначенных для отсечения помех от полезного сигнала.
Рассмотрим работу входной избирательной цепи приемника. На рис. 7.12 показана схема входной цепи приемника и ее эквивалентная схема. Схема входной цепи состоит из (см. рис. 7.12, а) антенны, заземления, конденсатора С и индуктивной катушки L, образующих колебательный контур, разделительного конденсатора Ср, обеспечивающего связь входной цепи с последующим каскадом.
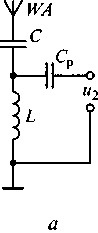
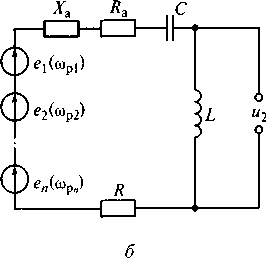
Рис. 7.12. Схема входной цепи приемника (а) и ее эквивалентная схема (б)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.