параллельного колебательного контура
определяются одним и тем же выражением для полосы пропускания: Δω =2 Δω1 = ω0/Q.
4. Рассматривая аргумент комплексного входного сопротивления параллельного контура, видим, что на частотах меньше резонансной ω< ω0 сопротивление контура носит резистивно-индуктивный характер. Напротив, на частотах больше резонансной ω > ω0 сопротивление контура имеет резистивно-емкостный характер.
Сравнивая входные сопротивления последовательного и параллельного колебательных контуров, отметим следующее.
1 . При резонансе входные сопротивления обоих контуров имеют активный характер: у последовательного контура оно минимально и равно сопротивлению потерь R, а у параллельного контура — максимально (Ro = p2/R).
2. Увеличение обобщенной расстройки контура ξ независимо от ее знака приводит к увеличению модуля комплексного входного сопротивления последовательного контура и уменьшению модуля входного сопротивления параллельного контура.
3. Расстройка частоты как для последовательного, так и для параллельного контуров делает их входные сопротивления комплексными. На частотах меньших резонансной комплексное входное сопротивление последовательного контура носит емкостный характер, а параллельного — индуктивный. На частотах больших резонансной комплексное входное сопротивление последовательного контура носит индуктивный характер, а параллельного — емкостный.
Добротность Q = Ic /Im = IL/ Imпараллельного контура на резонансной частоте определяется амплитудными значениями тока емкости Iс и индуктивности ILконтура на резонансной частоте и амплитудным значением тока Im потребляемого контуром на резонансной частоте.
Амплитудное значение напряжения, падающего на параллельном контуре на резонансной частоте, Um= Im R0= Imp2/R. С учетом этого получим значения амплитудных токов индуктивности и емкости на резонансной частоте Iс ≈IL= Um/ p = Imp/R. Откуда
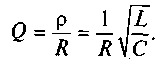(7.13)
Таким образом, добротности параллельного и последовательного колебательных контуров, состоящих из одних и тех же элементов, определяются одним и тем же выражением и равны между собой.
Анализируя влияние сопротивления нагрузки на добротность параллельного колебательного контура, отметим следующее.
1. Сопротивление потерь в контуре определяется суммой сопротивлений Rпот= R+Rп. C ростом Rп растет Rпот и соответственно уменьшается эквивалентная добротность Qэкв = p/(R + Rп) нагруженного контура.
2. Сопротивление потерь Rп, вносимое в контур сопротивлением нагрузки RH, обратно пропорционально сопротивлению нагрузки RH. Таким образом, с увеличением RHвносимое сопротивление потерь Rnуменьшается, а добротность Qконтура увеличивается.
3. Внутреннее сопротивление источника тока Ri являющегося источником входного сигнала, оказывает на добротность контура такое же влияние, что и RH.
4. Желая сохранить эквивалентную добротность контура на уровне добротности изолированного контура (7.13), необходимо стремиться к тому, чтобы сопротивление нагрузки и внутреннее сопротивление источника энергии были бы как можно больше.
7.7. Параллельный колебательный контур
с разделенной индуктивностью
Эквивалентная схема параллельного колебательного контура с разделенной индуктивностью представлена на рис. 7.16. Особенность этого контура состоит в том, что параллельно источнику тока включены две ветви. Одна из этих ветвей носит индуктивный характер (L1), а другая — индуктивно-емкостный характер (L2—C). Таким образом, энергия от источника тока поступает в точку соединения двух катушек индуктивности L1 и L2. Это приводит к отличию ряда параметров контура с разделенной индуктивностью от параметров параллельного контура основного вида (см. рис. 7.14). Докажем это.
В контуре с разделенной индуктивностью возникают два резонанса:
резонанс токов (параллельный колебательный контур) в контуре, индуктивность которого равна L = L1 + L2, а емкость С;
резонанс напряжений (последовательный колебательный контур), который возникает в контуре, состоящем из индуктивной катушки L2 и емкости С.
Так как энергия, подводимая к контуру, подается в разрыв катушки индуктивности, то в рассмотрение логично ввести коэффициент включения индуктивности
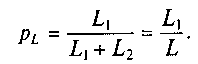(7.14)
При высокой добротности контура активные и реактивные сопротивления катушек индуктивности удовлетворяют условиям R1«ωL1, и R2«ωL2. Откуда комплексное входное сопротивление контура принимает вид
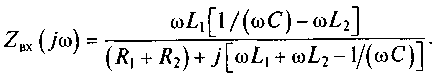(7.15)
При резонансе токов мнимая часть комплексного входного сопротивления контура должна быть равна нулю, т.е. ωL1 + ωL2 -1/(ωС) = 0. Отсюда находим, что частота резонанса токов
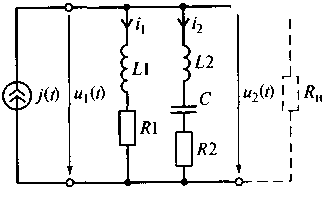
Рис. 7.16. Эквивалентная схема параллельного колебательного контура
с разделенной индуктивностью
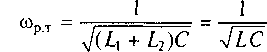
Из полученного выражения следует, что частота резонанса токов в контуре с разделенной индуктивностью совпадает с резонансной частотой последовательного и параллельного контуров основного вида при условии, что параметры элементов (L = L1 + L2 и С) во всех контурах совпадают.
Частота резонанса напряжений в параллельном контуре с разделенной индуктивностью ωP.H = 1/√(L2 C) определяется только индуктивностью L2и емкостью С.
В этом выражении индуктивность L2 представим в виде L - L1. Осуществив преобразования, получим еще одно выражение для описания частоты резонанса напряжений в контуре с разделенной индуктивностью:
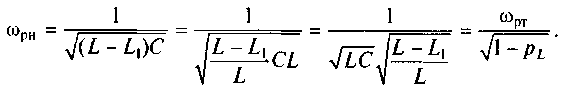
Таким образом, частота резонанса напряжений в контуре с разделенной индуктивностью зависит от коэффициента включения индуктивности (7.14). Согласно (7.14) коэффициент включения индуктивности pLможет изменяться от 0 при L1 = 0 до 1 при L1 = L. Из этого следует, что частота резонанса напряжений больше частоты резонанса токов.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.