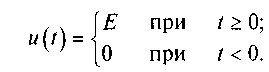
Так как рассматриваемая цепь не имеет потерь (внутреннее сопротивление источника напряжения Ri равно нулю), а идеализированный источник напряжения может отдать бесконечно большой ток без изменения выходного напряжения, то практически мгновенно на емкости установится напряжение uc(t), равное напряжению источника. Согласно (5.1) емкость будет заряжаться бесконечно большим током. При этом в емкости накапливается энергия конечной величины Wc=Cuc2(t)/2, вызывая появление ЭДС емкости ес. В соответствии с направлением протекания тока ic(t) в емкости ЭДС ес имеет такую же полярность, что и напряжение, приложенное к емкости (на верхней обкладке знак «+», а на нижней обкладке «-»). При этом напряжение uc(t) направлено от «+» к «-», а ЭДС емкости ес наоборот. Значит, ЭДС емкости имеет знак, противоположный знаку напряжения ис=-ес, и противодействует росту ис.
Так как рассматриваемая цепь не имеет потерь и до t= 0 никакого противодействия росту ис(t) нет (ес= 0), то скачок напряжения uc(t) вызывает появление бесконечно большого тока емкости ic(t).
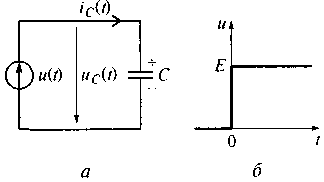
Рис. 5.7. Идеализированная цепь с емкостью (а) и источник напряжения (6)
В результате этого ЭДС емкости практически мгновенно достигает значения ес = ис, а значения ec(t) и uc(t) уравновешиваются и ток емкости iс(t) становится равным нулю.
Таким образом, подключение источника постоянного напряжения к емкости приводит к формированию бесконечно большого по амплитуде и бесконечно короткого по времени импульса тока.
На рис. 5.8 показана зависимость напряжения, тока, мощное и энергии от мгновенной фазы энергетических процессов в емкости. Пусть на емкость воздействует напряжение (см. рис. 5.8, а), представляющее собой гармоническую функцию:
uc(t)=Umcos(ωt+φи)=√2Ucos(ωt+φи).(5.5)
Используя выражение (5.1), можно найти ток емкости:
ic(t)=C(duc(t))/dt=-√2UCωsin(ωt+φи)=√2UCωcos(ωt+φи+π/2). (5.6)
Сравнивая выражения (5.5) и (5.6), видим, что начальная фаза гармонической функции, по которой изменяется ток емкости, равна φi=φи+π/2. Разность начальных фаз напряжения φи и тока φi
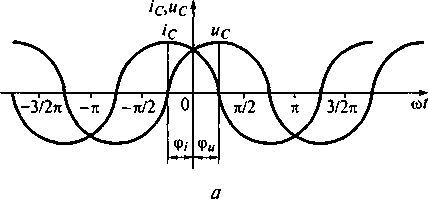
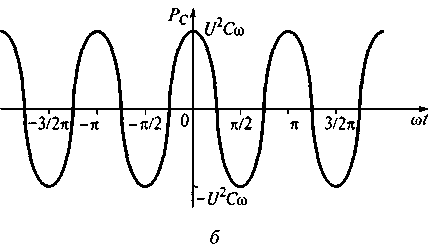
Рис. 5.8. Зависимость напряжения и тока (а) и мгновенной мощности (б)) от мгновенной фазы энергетических процессов в емкости
составляет φс= φи- φи-π/2= -π/2 Таким образом, ток емкости по фазе опережает напряжение на 90°.
Используя соотношения (5.5) и (5.6), находим мгновенную мощность емкости (см. рис. 5.8, б):
Pc (t) = uc (t)ic (t) = -√2Ucos(ωt+φи) √2UCωsin (ωt+φи) =-U2Csin (2ωt+2φи).
Анализируя полученное выражение, отметим следующее:
мгновенная мощность емкости изменяется по закону синуса с удвоенной круговой частотой;
так как функция синус за период изменения принимает значения от -1 до 1, то мгновенная мощность емкости изменяется от +U2Cω до -U2Cω. При этом средняя мощность равна нулю;
когда знаки напряжения и тока совпадают, то мощность емкости положительная и она накапливает энергию. Если же знаки напряжения и тока различны, то мгновенная мощность емкости отрицательная и она отдает энергию цепи;
с ростом частоты мощность емкости растет пропорционально частоте.
Известно, что гармоническая функция косинуса может быть представлена суммой показательных функций:
(5.7)
где exp(jx) и exp(-jx) — соответственно комплексное и комплексно сопряженное к нему числа. С учетом этого анализ радиотехнических цепей будет упрощен, если вместо функции косинуса применять показательную функцию ехр(jх). В этом случае обратный переход к гармонической функции может быть осуществлен в соответствии с формулой (5.7).
Используя показательную функцию exp(jx), напряжение и ток емкости можно представить в виде
Ũc=√2Uexp[j(ωt+φи)]=[√2Uexp(jφи)]exp(jωt); (5.8)
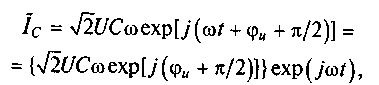(5.9)
где ехр(jωt) — единичный вектор вращения на комплексной плоскости, скорость вращения которого пропорциональна частоте ω. На рис. 5.9 показано расположение векторов комплексных амплитуд тока и напряжения емкости на комплексной плоскости.
В выражениях (5.8) и (5.9) величины в квадратных и фигурных скобках представляют собой комплексную амплитуду напряжения емкости Ůc = √2Uехр(jφи) и комплексную амплитуду тока емкости İс = √2UCехр[j(φи+π/2)].
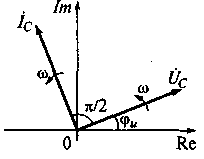
Рис. 5.9. Расположение векторов комплексных амплитуд тока и напряжения
емкости на комплексной плоскости
Комплексная амплитуда напряжения Ůс является постоянной величиной, зависящей только от постоянных гармонической функции Uи φи +. Комплексная же амплитуда тока емкости İс зависит как от постоянных составляющих гармонической функции Uи φи+π/2, так и от величины емкости С и круговой частоты ω. На комплексной плоскости (см. рис. 5.9) комплексные амплитуды представляются векторами, длина которых равна модулю комплексного числа. Относительно действительной оси вектор расположен под углом, равным аргументу комплексного числа.
Имея комплексные амплитуды напряжения и тока емкости, можно найти комплексное сопротивление емкости, т. е. сопротивление емкости переменному току:
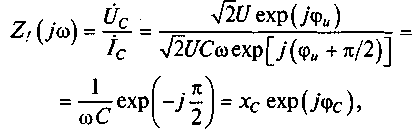
где φс=-π/2 — фазовый сдвиг между напряжением и током емкости. Рассматривая модуль комплексного сопротивления емкости (полное сопротивление) хс= 1/(ωС), видим, что он обратно пропорционален круговой частоте ω. Чем больше частота, тем меньше полное сопротивление емкости.
5.6. Подключение индуктивности к различным источникам тока
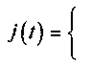Пусть имеется идеализированная цепь из
последовательно соединенных индуктивности и источника тока (рис. 5.10),
значение тока которого описывается выражением (см. рис. 5.10, б)
Iпри t ≥ 0;
О при t < 0.
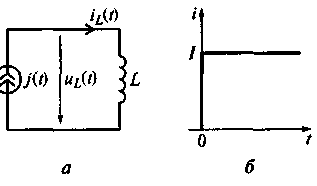
Рис. 5.10. Идеализированная цепь из последовательно соединенных индуктивности и источника тока (а) и зависимость тока цепи от времени (б)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.