параметрами — сопротивление провода RLи межвитковая емкость CL. Наличие включенных параллельно индуктивности и емкости приводит к тому, что при определенной частоте модуль комплексного сопротивления индуктивности будет равен модулю комплексного сопротивления емкости. При дальнейшем увеличении частоты комплексное сопротивление индуктивной катушки будет носить не индуктивный, а емкостной характер, т.е. индуктивная катушка перестает выполнять свои свойства индуктивности.
Конденсаторы делят на категории в основном по типу используемого диэлектрика. Конденсатор обладает емкостью С, индуктивностью выводов и внутренней структуры конденсатора Lc, сопротивлением RI, зависящим от тангенса угла диэлектрических потерь, и сопротивлением утечки R2 (см. рис. 5.5, в). Наличие в модели конденсатора соединенных последовательно индуктивности и емкости приводит к возникновению в конденсаторе последовательного резонанса на определенной частоте. В этом случае полное сопротивление конденсатора может достигать минимальной величины. При дальнейшем увеличении частоты комплексное сопротивление конденсатора начинает носить индуктивный характер, т.е. конденсатор теряет свои емкостные свойства.
5.3. Идеализированное сопротивление
Идеализированным сопротивлением Rэлектрической цепи называется параметр реального двухполюсника, который характеризует преобразование подводимой к двухполюснику электрической энергии в тепловую или световую энергии и полностью рассеивает их. Схема электрической цепи с сопротивлением, графики изменения напряжения и тока на внешних зажимах сопротивления, а также мощности, рассеиваемой сопротивлением, показаны на рис. 5.6.
На рис. 5.6, а показана цепь, состоящая из генератора напряжения и подключенного к нему сопротивления R. Напряжение в цепи u(t) определяется по выражению
![]()
где Umи U = Um/ √2 — амплитудное и действующее значения напряжения соответственно; ω и φи — круговая частота и начальная фаза гармонической функции соответственно.
Согласно закону Ома в этой цепи возникает ток
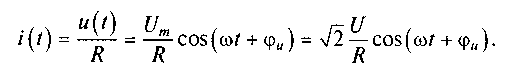
Рассматривая выражения для определения напряжения и тока, видим, что в сопротивлении напряжение (см. рис. 5.6, б) и ток (см. рис. 5.6, в) совпадают по фазе,
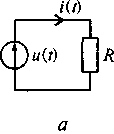
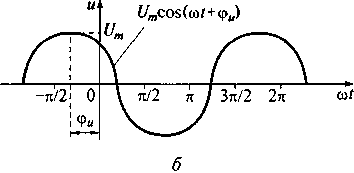
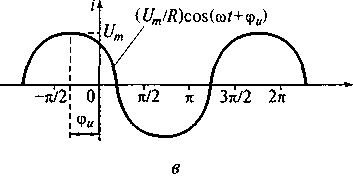
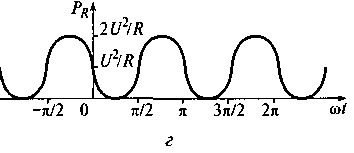
Рис. 5.6. Схема электрической цепи с сопротивлением (а); графики изменения напряжения (б) и тока (в) на внешних зажимах сопротивления, мощности,
рассеиваемой сопротивлением (г)
имея одно и то же значение ср„. Направление протекания тока и напряжения в сопротивлении совпадают, поэтому мгновенная мощность в сопротивлении
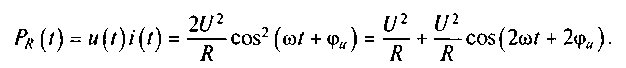
Из этого выражения видно, что мгновенная мощность в сопротивлении включает постоянную составляющую U2/Rи переменную составляющую (U2/R)cos(2ωt + 2φи), значение которой изменяется с удвоенной частотой (см. рис. 5.6, г). Так как в зависимости от аргумента косинус может изменяться от -1 до 1, то максимальное значение мгновенной мощности в сопротивлении равно 2U2/R, а минимальное равно нулю. Среднее значение мгновенной мощности в сопротивлении за определенный период равно U2/R. Таким образом, мгновенная мощность в сопротивлении всегда положительная.
5.4. Идеализированные реактивные двухполюсники
Идеализированные пассивные реактивные двухполюсники отличаются от сопротивления тем, что способны накапливать энергию электромагнитного поля, а затем возвращать ее в цепь, не рассеивая. Подобное свойство реального конденсатора характеризуется таким параметром, как емкость, а для реальной индуктивной катушки индуктивностью.
Мгновенное значение тока ic(t) емкости и мгновенное значение напряжения uc(t) на ее зажимах связаны между собой соотношениями:
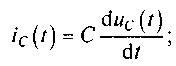 (5.1)
(5.1)
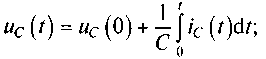 (5.2)
(5.2)
где uc(0)=(1/C)∫-∞0ic(t)dt — напряжение, которое присутствует на емкости за счет заряда, накопленного в ней к моменту t = 0.
Мгновенное значение тока iL(t) в индуктивности и мгновенное значение напряжения uL(t) на ней связаны между собой соотношениями:
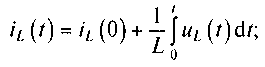 (5.3)
(5.3)
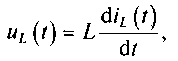 (5.4)
(5.4)
где iL(0)=(1/L)∫-∞0uL(t)dt — ток, который может протекать через индуктивность до начала рассматриваемого интервала времени [0, t]. Из соотношений (5.1) — (5.4) видно, что конденсатор накапливает энергию электрического поля, а индуктивная катушка накапливает энергию магнитного поля. Это позволяет сформулировать ряд следующих свойств этих элементов.
1. При приложении к конденсатору внешнего напряжения в нем накапливается энергия электрического поля. Это приводит к возникновению на внешних зажимах конденсатора ЭДС емкости ес. При приложении к индуктивной катушке внешнего напряжения через нее протекает ток, который приводит к накоплению энергии магнитного поля и возникновению ЭДС самоиндукции еLна внешних зажимах индуктивной катушки. Напряжения, прикладываемые к внешним зажимам конденсатора ис и индуктивной катушки ul, являются первичными, а ЭДС ес и eL, возникающие в них, — вторичными. При этом ис=-ес и uL =-eL.
2. При работе радиотехнической цепи часто возникает ситуация, когда напряжения uL и (или) ис направлены от индуктивной катушки и (или) конденсатора к другим элементам цепи (например, колебательный контур). В этом случае индуктивная катушка и (или) конденсатор будут выполнять роль вторичных источников энергии, отдающих энергию цепи. Это приводит к тому, что первичные и вторичные ЭДС попеременно противодействуют друг другу, уменьшая амплитуду тока в цепи при заданной частоте ω и амплитуде Umсигнала.
5.5. Подключение емкости к различным источникам напряжений
Пусть имеется идеализированная цепь, включающая емкость и источник напряжения (рис. 5.7). В момент времени t= 0 напряжение источника изменяется от нуля до Е (см. рис. 5.7, б):
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.