Линейные цепи с сосредоточенными параметрами. Линейные четырехполюсники. Колебательные контуры (5-7 главы учебника "Радиотехнические цепи и сигналы" под ред. К.Е.Румянцева), страница 22

              Сопротивления потерь в первой R₁ и во второй R₂ветвях кон­тура существенно меньше реактивных сопротивлений емкости первой ветви С₁, индуктивности Lи емкости С₂ второй ветви. Тогда входное сопротивление контура на частоте резонанса токов ω _рт составит

где R₀ = r²/R — сопротивление параллельного контура основного вида на резонансной частоте.

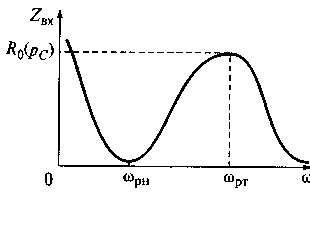
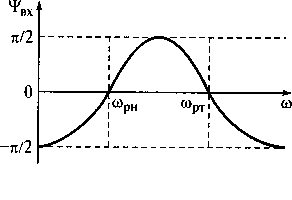
                На рис. 7.19 показаны модуль и аргумент входного сопротив­ления параллельного колебательного контура с разделенной ем­костью.

                В диапазоне частот 0 < ω < ω_рн модуль комплексного входного сопротивления контура (см. рис. 7.19, а) определяется в основном реактивными сопротивлениями емкостей С1 и С2 (см. рис. 7.18).

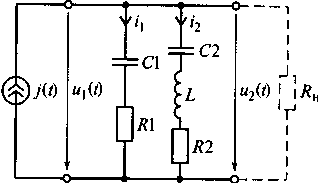
Рис. 7.18. Эквивалентная схема па­раллельного колебательного

конту­ра с разделенной емкостью

При ω = ω_рн величина Z_BX(ω) достигает минимального значе­ния, определяемого сопротив­лением потерь R₂.

               Аргумент комплексного вход­ного сопротивления (см. рис. 7.19, б) при приближении час­тоты ω к нулю равен -π/2, но по мере увеличения частоты он снижается и обращается в нуль при ω = ω_рн.

В диапазоне частот ω_рн< ω <ω_pт модуль комплексного вход­ного сопротивления контура носит резистивно-индуктивный ха­рактер и определяется в основном второй ветвью контура, вклю­чающей С2 и L. Аргумент комплексного входного сопротивления по мере возрастания частоты ω > ω_рн также возрастает и, достигнув угла π/2, начинает снижаться, обращаясь в нуль на частоте ω = ω_рт.

               На частоте резонанса токов ω = ω_рт модуль комплексного вход­ного сопротивления контура достигает максимального значения r₀ (p_c), а аргумент обращается в нуль. На частотах ω > ω_рт модуль комплексного входного сопротивления контура носит резистив-но-емкостной характер и по мере увеличения частоты снижается до уровня сопротивления потерь контура. При этом аргумент дос­тигает величины -π/2.

               В контуре с разделенной емкостью входное сопротивление кон­тура на частоте резонанса токов зависит от коэффициента вклю­чения емкости р_с.

Эта зависимость позволяет согласовать сопротивление r₀ (p_c) контура на резонансной частоте с сопротивлением нагрузки R_H.Подобное согласование может быть произведено, например, для обеспечения требуемой добротности контура.

                 

а                                                              б

Рис. 7.19. Модуль (а) и аргумент (б) входного сопротивления

параллель­ного колебательного контура с разделенной емкостью

7.9. Связанные колебательные контуры

                 В радиотехнических цепях достаточно часто применяются свя­занные колебательные контуры. Они позволяют повысить избира­тельные свойства (усиление гармонических составляющих вход­ного сигнала) колебательных систем. К подобным цепям относят фильтры, входные цепи радиоприемников и др.

                  Под связанным колебательным контуром понимают систему, состоящую из двух контуров. Оба контура могут быть колебатель­ными, либо один из них колебательный, а другой апериодиче­ский. Особенность связанных контуров заключается в том, что при возбуждении электрических колебаний в одном из контуров элек­трические колебания возникают и в другом контуре.

                  Известны последовательные и параллельные одиночные коле­бательные контуры. В качестве элементов связи в связанных кон­турах могут быть использованы взаимная индуктивность между катушками, индуктивные катушки и конденсаторы. Элементы связи могут как непосредственно входить в первый и второй колеба­тельные контуры и определять их параметры (внутренняя связь), так и не входить непосредственно в колебательные контуры (вне­шняя связь). Наличие различных контуров, элементов связи и ва­риантов организации электрической связи между контурами по­зволяет говорить о множестве возможных вариантов организаций связанных контуров. На рис. 7.20 показаны эквивалентные элект­рические схемы связанных контуров с различными связями.

              Важной характеристикой связанных контуров является коэф­фициент связи

                                                           k_CB= х_св/√(x₁x₂)                                                     (7.18)

где х_св — реактивное сопротивление элемента связи; х₁ и х₂ — реактивные сопротивления первого и второго контуров, имею­щие тот же знак, что и реактивное сопротивление элемента связи.

             Используя выражение (7.18), запишем значения коэффициентов связи для четырехполюсников связи, представленных на рис. 7.20:

трансформаторная связь k_CB=

внутренняя индуктивная связь k_CB =

внешняя индуктивная связь k_CB =

внутренняя емкостная связь k_CB =

внешняя емкостная связь k_CB=

комбинированная связь k_CB=

д                                                                        е

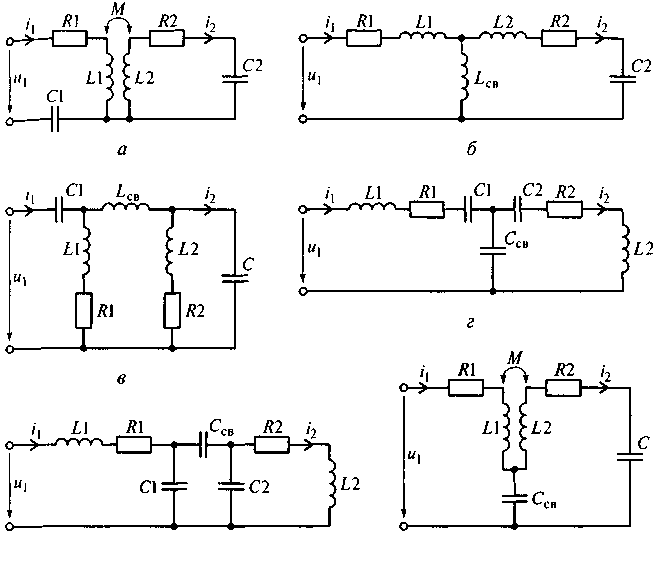
Рис. 7.20. Эквивалентные электрические схемы связанных контуров:

а - с трансформаторной связью; б — с внутренней индуктивной связью;

в — с внешней индуктивной связью; г — с внутренней емкостной связью;

д — с внешней емкостной связью; е — с комбинированной связью

              Анализируя выражения для определения коэффициентов связи четырехполюсников, можно говорить о следующих их свойствах:

               коэффициенты связи при различных вариантах организации че­тырехполюсников связи (кроме комбинированной) не зависят от частоты, а определяются только вариантом соединения и парамет­рами реактивных элементов, входящих в четырехполюсник связи;

               при увеличении параметра элемента связи М, L_CB или С_CB в связанных контурах с трансформаторной, внешней емкостной и комбинированной связями коэффициент связи возрастает;

               при увеличении параметра элемента связи L_CB или С_CB в связан­ных контурах с внешней индуктивной и внутренней емкостной связями коэффициент связи уменьшается;

               коэффициент связи не может быть больше единицы.

               Рассматривая варианты построения связанных контуров в це­лях их наиболее эффективного использования, необходимо от­ветить на два основных вопроса.