Линейные цепи с сосредоточенными параметрами. Линейные четырехполюсники. Колебательные контуры (5-7 главы учебника "Радиотехнические цепи и сигналы" под ред. К.Е.Румянцева), страница 11

                 Представим КЧХ в показательной форме:

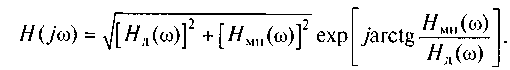
                 Из полученного выражения видно, что КЧХ включает две со­ставляющие:

амплитудно-частотную характеристику цепи, определяемую модулем КЧХ

и отражающую зависимость от частоты сигнала амплитуды отклика цепи;

            фазочастотную характеристику цепи, определяемую аргументом  КЧХ

 φ(ω) = arctg|H_МН(ω)/ H_Д(ω)|от частоты фазы отклика цепи.

            Рассмотрим возможные виды КЧХ. В качестве входного воздей­ствия относительно зажимов 1 — 1 четырехполюсника может выс­тупать как напряжение Ů₁ , так и ток İ₁ . Тогда откликом цепи относительно зажимов 1 — 1 в первом случае будет ток İ₁, а во втором — напряжение Ů₁. С учетом этого в качестве КЧХ цепи относительно зажимов 1 — 1 могут быть:

входное сопротивление

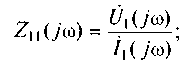                                                                          (6.1)

входная проводимость

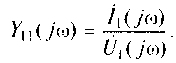                                                                               (6.2)

           Используя в качестве входных зажимы 1 — 1, а выходных  зажимы 2 — 2, можно заметить следующее. Откликом цепи могут быть как напряжение Ů₂, так и ток İ₂. В качестве входного воз­действия также могут выступать как напряжение Ů₁ , так и ток İ₁. В этом случае можно получить четыре передаточные КЧХ от зажи­мов 1 — 1 к зажимам 2 — 2:

           коэффициент передачи по напряжению

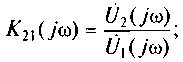                                                                                 (6.3)

коэффициент передачи по току

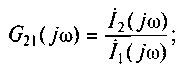                                                                               (6.4)

передаточное сопротивление

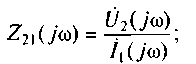                                                                             (6.5)

передаточная проводимость

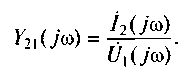                                                                              (6.6)

              Таким образом, используя зажимы 1 — 1 в качестве входных, а 2 —2 в качестве выходных, можно получить две входные КЧХ (6.1) и (6.2) и четыре передаточные КЧХ (6.3) — (6.6). Смена местами зажимов 1 — 1 и 2 — 2 позволяет получить еще две входные КЧХ Z₂₂( jω) и Y₂₂(jω) и четыре передаточные КЧХ K₁₂(jω), G_I2(jω), Z₁₂(jω) и Y₁₂(jω).

             Применительно к КЧХ можно отметить следующее.

    1. Так как отклик цепи Ś(jω)и входное воздействие X^´( jω) в общем виде являются комплексными величинами и могут быть представлены в показательной форме Ś(jω)= S(ω)ехр(jψ_S), Х^´(jω)=X(ω)exp (jψ_x), то АЧХ отражает отношение амплитуд­ных или действующих значений отклика цепи и входного воздей­ствия, а ФЧХ — разность фаз отклика цепи и входного воздей­ствия, т. е. φ = ψ_S-ψ_x.

     2. Несмотря на то что КЧХ отражает отношение отклика цепи к входному воздействию, она не зависит от комплексных ампли­тудных или комплексных действующих значений напряжений и токов, а определяется только типом элементов, входящих в цепь (сопротивление, емкость, индуктивность), топологией цепи (по­рядок соединения элементов между собой) и частотой внешнего воздействия.

     3. Найти КЧХ можно, определив одним из доступных способов отклик цепи в соответствии с известным входным воздействием и вычислив отношение отклика цепи к входному воздействию.

Пример 6.3. На рис. 6.4 показаны схема электрической цепи и ее ком­плексная схема замещения. Для цепи (см. рис. 6.4, а) известно, что в качестве входного воздействия выступает напряжение u₁. Необходимо определить частотную зависимость параметров Z₁₁(jω) и K₂₁(jω) элект­рической цепи, АЧХ и ФЧХ, отмеченных параметров цепи.

          Решение. Составим комплексную схему замещения этой цепи (см. рис. 6.4, б), заменив индуктивность и сопротивление их комплекс­ными сопротивлениями.

          Так как сопротивление нагрузки относительно зажимов 2 — 2 отсут­ствует, то можно считать, что İ₂ = 0 . Напряжение Ů_lизвестно. Исполь­зуя закон Ома, определяем величину тока İ₁ = Ů₁/(Z_R + Z_L). Тогда можно найти входное сопротивление цепи

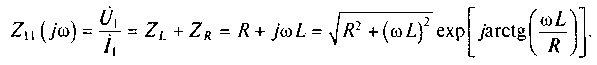
           Рассматривая комплексную схему замещения (см. рис. 6.4, б) как делитель напряжения, можно определить напряжение Ů₂ =Ů₁ Z_R/(Z_R +Z_L). Зная напряжения Ů₁ и Ů₂, найдем комплекс­ный коэффициент передачи напряжения цепи

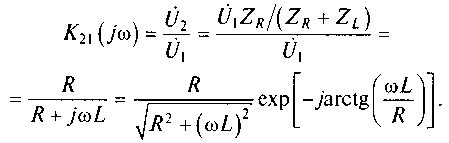
            Рассматривая АЧХ и ФЧХ различных КЧХ, найденных при решении примера 6.3, отметим следующие особенности:

            модуль входного сопротивления цепи Z₁₁ (ω) = √(R² + (ωL)²)    ра­стет с ростом частоты ω. На рис. 6.5 показаны АЧХ и ФЧХ входного сопротивления цепи,

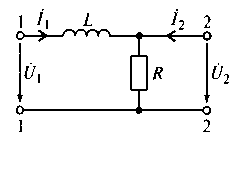
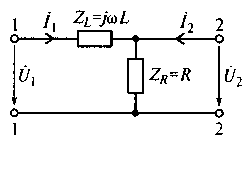
а                                         б

Рис. 6.4. Схема электрической цепи (а) и ее комплексная схема замеще­ния (б)

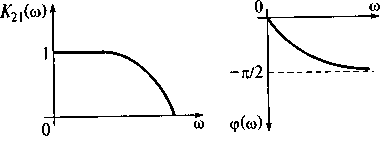
а                                  б

Рис. 6.5. АЧХ (а) и ФЧХ (б) входного сопротивления цепи

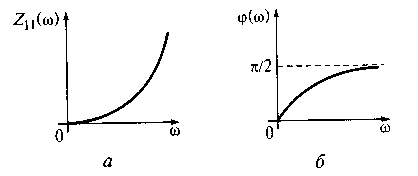
Рис. 6.6. АЧХ (и) и ФЧХ (б) коэффициента передачи напряжения

а на рис. 6.6 АЧХ и ФЧХ коэффициента передачи напряжения. При ωL > Rрост АЧХ идет практически пропорционально частоте (см. рис. 6.5, а). ФЧХ этой КЧХ φ(ω) = arctg(ωL/R) растет от нуля при ω = 0 до 90° при ω, стремящейся к бесконечности (см. рис. 6.5, б);

       модуль коэффициента передачи  напряжения    К₂₁(ω) =R/√(R² + (ωL)²) с ростом частоты ω уменьшается (см. рис. 6.6, а), а ФЧХ φ(ω) = -arctg(ωL/R) изменяется от нуля при

ω = 0 до -90° при частоте ω, стремящейся к бесконечности (см. рис. 6.6, б).

6.4. Связь комплексных частотных характеристик

с первичными параметрами четырехполюсника

             Наибольший практический интерес представляет определение связи между различными КЧХ и первичными параметрами четы­рехполюсника, у которого к зажимам 2 — 2 подключено сопро­тивление нагрузки Z_H2, а к зажимам 1 — 1 подключен генератор напряжения E_rс внутренним сопротивлением Z_r. На рис. 6.7 по­казана электрическая цепь для определения рабочих характерис­тик четырехполюсника.

            Комплексные частотные характеристики проходного четырех­полюсника при произвольном сопротивлении нагрузки удобно рассматривать, используя A-параметры четырехполюсника. Применим систему уравнений, описывающую четырехполюсник от­носительно A-параметров (см. табл. 6.1).

            В  исходной  системе уравнений произведем  замену Ů₁ = Ė_r - İ₁ Zr, İ^´₂= Ů₂/Z_H2и Ů₂= Z_H2İ₂ . В результате имеем