Это — идеализированная цепь, в которой отсутствуют потери (внутреннее сопротивление источника тока равно бесконечности, сопротивление провода индуктивной катушки равно нулю). Поэтому весь ток источника в момент времени t = 0 прикладывается к индуктивности. Ток, протекающий через индуктивность, вызывает скачок напряжения
ul(t) = L(diL(t)/dt) на ней при t = 0.
За счет действия тока в индуктивности накапливается энергия конечной величины WL= Li2L(t)/2.
ЭДС самоиндукции eL = -uLимеет знак, противоположный напряжению ul, приложенному к зажимам индуктивности, так как она препятствует росту потокосцепления в индуктивности. Достигнув бесконечно большой величины, напряжение на индуктивности резко снижается до нуля.
Таким образом, подключение источника постоянного тока к индуктивности приводит к формированию бесконечно большого по амплитуде и бесконечно короткого по времени импульса напряжения.
На рис. 5.11 показана зависимость тока, напряжения, мощности и энергии в индуктивности от мгновенной фазы входного сигнала.
Рассмотрим индуктивность при воздействии на нее тока, представляющего собой гармоническую функцию (см. рис. 5.11, а):
![]() (5.10)
(5.10)
В соответствии с (5.4) найдем напряжение на индуктивности (см. рис. 5.11, а):
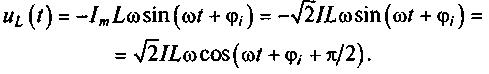 (5.11)
(5.11)
Сравнивая выражения (5.10) и (5.11), видим, что фазовый сдвиг напряжения на зажимах индуктивности φи=φi+π/2, т.е. напряжение на угол π/2 опережает ток. Таким образом, ток индуктивности на 90° отстает от напряжения на ее зажимах.
В соответствии с выражениями (5.10) и (5.11) мгновенная мощность индуктивности имеет вид (см. рис. 5.11, б)
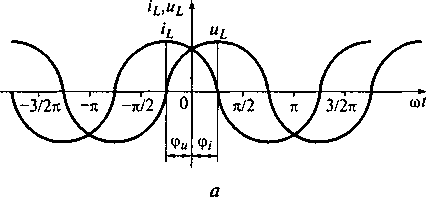
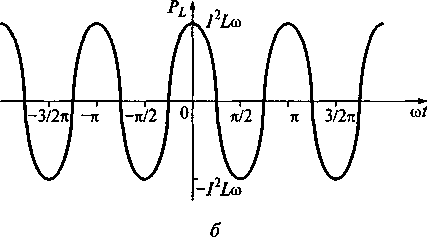
Рис. 5.11.Зависимость тока и напряжения (а) и мгновенной мощности (б)
в индуктивности от мгновенной фазы
PL (t)=uL(t)iL(t)=-√2ILωsin(ωt+φi)√2Icos (ωt+φi)=-I2Lωsin (2ωt+2φi).
Анализируя полученное выражение, отметим следующее:
мгновенная мощность индуктивности изменяется по закону синуса с удвоенной частотой 2ω по сравнению с частотой источника тока;
функция синус изменяется от -1 до 1, поэтому мгновенная мощность индуктивности принимает значения от I2Lω до -I2Lω. Соответственно средняя мощность индуктивности равна нулю;
если знаки напряжения и тока индуктивности совпадают, то мощность индуктивности положительна и она накапливает энергию. Когда знаки различны, то мгновенная мощность индуктивности отрицательна и она отдает энергию цепи;
с ростом частоты мгновенная мощность индуктивности растет пропорционально частоте.
Комплексные амплитуды тока и напряжения индуктивности в соответствии с (5.10) и (5.11) описываются формулами:
![]() (5.12)
(5.12)
![]() (5.13)
(5.13)
Из формул (5.12) и (5.13) видно, что комплексная амплитуда тока определяется постоянными гармонической функции I и φi, a комплексная амплитуда напряжения зависит как от постоянных гармонических функций I и φi +π/2, так и от индуктивности Lи круговой частоты ω. Имея комплексные амплитуды напряжения (5.12) и тока (5.13) индуктивности, можно найти ее комплексное сопротивление
ZL=ŮL/ İL=( √2ILωexp[j(φi +π/2)])/( √2Iexp(jφi))=ωLexp(jπ/2)=xLexp(jφL),
где φL= π/2 — фазовый сдвиг между напряжением и током индуктивности.
Модуль комплексного сопротивления индуктивности xl= ωL прямо пропорционален частоте. Чем выше частота, тем больше полное сопротивление индуктивности.
5.7. Конденсатор при приложении к нему напряжений различной формы
На рис. 5.5, в приведена модель конденсатора, включающая как емкость С, характеризующую способность конденсатора накапливать энергию электрического поля, так и ряд паразитных элементов. Это индуктивность Lcвыводов и обкладок конденсатора, сопротивление RIвыводов и обкладок конденсатора и сопротивление R2 утечек диэлектрика. Наличие паразитных элементов в конденсаторе приводит к тому, что подводимая к конденсатору энергия не только накапливается в нем, но и частично рассеивается. Кроме того, при превышении определенной частоты сигнала конденсатор теряет свои основные свойства.
На рис. 5.12 показаны модель конденсатора с идеализированным генератором напряжения, а также форма воздействующего напряжения и преобразованная модель конденсатора.
В соответствии с моделью конденсатора (см. рис. 5.12, а) рассмотрим его работу при приложении различных по форме напряжений внешних воздействий.
Применяя к параллельно соединенным сопротивлению R2 и емкости С в модели конденсатора преобразования, позволяющие перейти к последовательной схеме замещения сопротивления и емкости, получим эквивалентную модель конденсатора (см. рис. 5.12, в), в которой
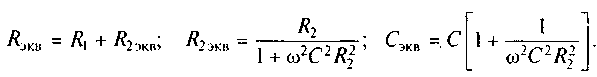
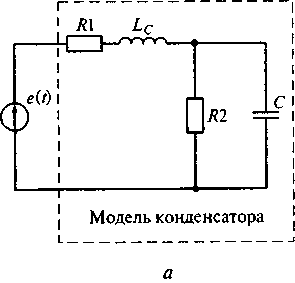
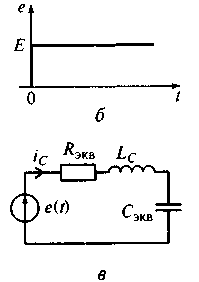
Рис. 5.12. Модель конденсатора с идеализированным генератором напряжения (а), форма воздействующего напряжения (б) и преобразованная модель конденсатора (в)
В реальном конденсаторе R2« R1, поэтому можно считать, что потери конденсатора в большей мере определяются сопротивлением выводов и обкладок конденсатора R1. Заметим, что на резонансной частоте ω0 = l/√LcCэкв полное сопротивление конденсатора равно R1.
Пусть к конденсатору в момент времени t = 0 приложено напряжение e(t) вида (см. рис. 5.12, б)

В зависимости от соотношения между коэффициентом затухания δ = Rэкв/(2LC) и резонансной частотой ω0 можно рассмотреть три случая зависимости тока конденсатора от времени.
1. При равенстве коэффициента затухания и резонансной частоты δ=ω0 ток конденсатора описывается выражением
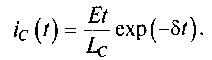
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.