Линейные цепи с сосредоточенными параметрами. Линейные четырехполюсники. Колебательные контуры (5-7 главы учебника "Радиотехнические цепи и сигналы" под ред. К.Е.Румянцева), страница 17

Рис. 7.8. Зависимости реактивных сопротивлений индуктивности и емкости (а), модуля комплексного входного сопротивления (б) и ар­гумента (в) последовательного контура от частоты

1.При изменении частоты от 0 до ω₀ входное сопротивление является резистивно-емкостным и изменяется от ∞ до R, а аргу­мент изменяется от -90° при ω = 0 до 0° при ω = ω₀.

2.При изменении частоты от ω₀ до ∞ входное сопротивление является резистивно-индуктивным и изменяется от R до ω, а ар­гумент изменяется от 0° при ω = ω ₀ до 90° при частоте ω, стремя­щейся к бесконечности.

3. На резонансной частоте ω = ω ₀ входное сопротивление является чисто резистивным и равно R, а аргумент равен нулю.

               Таким образом, на резонансной частоте напряжение и ток на входных зажимах последовательного колебательного контура совпа­дают по фазе.

               На резонансной частоте ω ₀ модуль входного сопротивления контура равен сопротивлению потерь R. Комплексное входное напряжение полностью приложено к R, aток, протекающий в цепи, будет иметь вид

İ_m=Ů_m/R=(U_m/R)exp(jψ_u).

                С учетом того, что реактивные сопротивления индуктивности и емкости на резонансной частоте равны характеристическому сопротивлению контура, можно найти амплитуды комплексных напряжений на индуктивности и емкости:

               Добротность последовательного контура на резонансной час­тоте равна отношению амплитуды напряжения, падающего на реактивном элементе, к амплитуде напряжения, приложенного к входным зажимам колебательного контура. Откуда

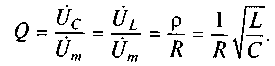
               Полученное выражение определяет зависимость добротности последовательного колебательного контура от параметров его эле­ментов. Из него видно, что изменение любого из параметров эле­ментов R, L или С контура может привести как к увеличению, так и к уменьшению его добротности.

                В реальных цепях ширина спектра радиосигналов не превыша­ет единиц процентов от резонансной частоты колебательных кон­туров. С учетом этого определенный интерес представляет зависи­мость от частоты модуля входного сопротивления последователь­ного контура в окрестности резонансной частоты.

                Комплексное входное сопротивление контура описывается выражением (7.8), в котором частота ω представляет собой часто­ту генератора напряжения входного сигнала. Пусть резонансная частота контура ω₀ = 1 / √(L/С) . Так как Q = p/R и р = ω₀L, то выра­жение (7.8) может быть преобразовано к виду

Z_вх(jω)=R[1+j(ω₀L/R)(( ω/ω₀)-(1/(ωω₀CL)))]=R[1+jQ((ω/ω₀)-( ω₀/ω))] .

            Введем понятие обобщенной расстройки

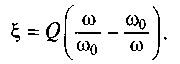                                                                                                  (7.9)

               Тогда формула для расчета комплексного входного сопротив­ления принимает вид

                При абсолютных отклонениях частоты источника сигнала от резонансной частоты контура Δω= ω-ω₀, удовлетворяющих усло­вию |Δω|«ω₀, можно полагать, что ω + ω₀= 2ω₀. Тогда

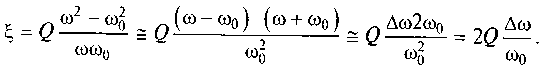
               Комплексное сопротивление контура принимает вид

Z_вх(jω)=R(1+j2Q(Δω/ω₀)).

               Модуль и аргумент входного сопротивления контура в соответ­ствии с его относительной расстройкой могут быть рассчитаны по формулам:

                                                                                         (7.10)

                                                                                         (7.11)

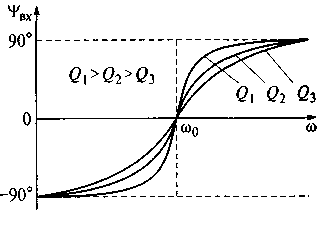
               Из формул (7.10) и (7.11) видно, что чем выше добротность контура, тем круче рост кривых, характеризующих модуль и аргу­мент входного сопротивления. На рис. 7.9 показаны зависимости модуля и аргумента входного сопротивления последовательного контура от частоты.

               Недостатком последовательного контура при его анализе в со­ответствии с формулами (7.10) и (7.11) является то, что прихо­дится оперировать всеми параметрами элементов контура. Этого можно избежать, рассматривая зависимость модуля и аргумента входного сопротивления контура от обобщенной расстройки ξ.

                Под передаточными характеристиками последовательного кон­тура будем понимать АЧХ и ФЧХ контура. Входное напряжение прикладывается к зажимам 1 — 1 (см. рис. 7.7) контура. Выходной сигнал можно снимать относительно реактивного сопротивления как емкости Z_c= 1/jωС = (1/ωС)ехр(-jπ/2), так и индуктивности Z_L=jωL = ехр(jπ/2). К этим сопротивлениям будут прикладывать­ся выходные напряжения, амплитуды которых U_cи U_Lимеют равные значения только на резонансной частоте. Тогда АЧХ контура характеризуется отношением амплитудных значений напряжений на реактивном элементе и входе контура К_с(ω) = U_c/U_m, k_l(ω) = = U_L/ Um, a ФЧХ — суммой фаз реактивных сопротивлений емкости или индуктивности и входного сопротивления

                                                  а                                                     б

Рис. 7.9. Зависимости модуля (а) и аргумента (б) входного

сопротивле­ния контура от частоты

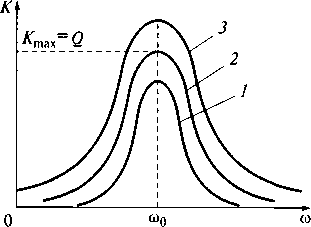
Рис.7.10. АЧХ последовательного колебательного контура

контура ψ_c(ω) =ψ_вх(ω)-π/2, ψ_L( ω) = ψ_вх(ω)+π/2. Анализ АЧХ последовательного колебательного контура (рис. 7.10) относительно емкости К_с(ω) и индуктивности K_L(ω) позволил установить следующие законо­мерности.

        1. Частоты ω_с = ω₀√(1-(1/(2Q)²) и ω_L = ω₀/√(1-(1/(2Q)²), на которых К_с(ω) и K_L(ω) достигают максимального значения, не совпадают.

        2.  Максимальные значения К_с(ω_с) и K_L(ω_L) равны между собой.

        3. Добротность колебательного контура имеет большое значение (50... 300), поэтому можно считать, что ω_с≈ ω_L = ω₀. Например, при Q= 10 находим ω_с = ω₀ √(1 -0,0025) ≈ ω₀ и

ω_L = ω₀ √(1 -0,0025) ≈ ω₀.

        4.  Максимальный коэффициент передачи в контуре достигается на резонансной частоте ω ₀ и равен добротности контура К_тaх = Q(кривая 2 на рис. 7.10). При расстройке контура от резонансной частоты ω ₀ в сторону увеличения или уменьшения частоты АЧХ контура резко снижается.

        5.  При увеличении сопротивления потерь Rдобротность конту­ра снижается Q= p/R. Максимальное значение коэффициента пе­редачи напряжения на резонансной частоте ω ₀ уменьшается про­порционально росту сопротивления потерь R. Кривая, описываю­щая АЧХ коэффициента передачи, становится более пологой (кри­вая 1 на рис. 7.10).