На рис. 5.13 показана временная зависимость тока конденсатора при значении коэффициента затухания не меньше резонансной частоты. Максимальный ток достигается в момент t1 = 1/δ и составляет icmах = (E/δLс)ехр(-1) = 0,184E/R1. Видно, что наличие сопротивления выводов и обкладок конденсатора приводит к ограничению максимального тока конденсатора на уровне 0,184E/R1. В то же время ток емкости при приложении к ней броска напряжения стремится к бесконечности. Таким образом, в конденсаторе определенная доля энергии теряется на сопротивлениях выводов и обкладок.
2. В случае, когда коэффициент затухания больше резонансной частоты δ > ω0, ток конденсатора имеет вид
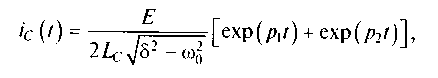
где p1=-δ+√(δ2-ω02) и p2=-δ-√(δ2-ω02).
Для второго случая ток конденсатора обратно пропорционален сопротивлению R1. Чем выше сопротивление потерь в конденсаторе, тем ниже ток.
3. Если коэффициент затухания меньше резонансной частоты δ < ω0, то ток конденсатора описывается выражением
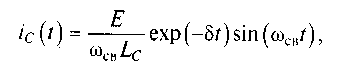
где ωсв = √(ω02-δ2) — частота свободных колебаний в конденсаторе.
Величина Im = (E/ ωсв Lc) exp(-δt) характеризует процесс затухания переходного колебательного процесса в конденсаторе, а сомножитель sin(a)c,,/) говорит о том, что переходной процесс в конденсаторе изменяется по гармоническому закону. На рис. 5.14 показана временная зависимость тока емкости конденсатора при значении коэффициента затухания меньше резонансной частоты.
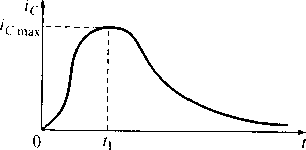
Рис. 5.13. Временная зависимость тока конденсатора при значении коэффициента затухания не меньше резонансной частоты
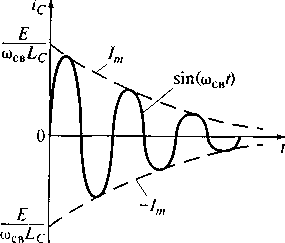
Рис. 5.14. Временная зависимость тока емкости конденсатора при значении коэффициента затухания меньше резонансной частоты
Таким образом, при условии R1< 2√(Lc/C) ток в конденсаторе при приложении к нему скачка напряжения представляет собой затухающий колебательный процесс. Чем меньше сопротивление R1 тем колебательный процесс затухает медленнее. Это может привести к излучению электромагнитной энергии конденсатором и установлению паразитных обратных связей между элементами реального радиотехнического устройства. Кроме того, во всех трех рассмотренных случаях отмечено, что часть энергии, подводимой к конденсатору, рассеивается, что приводит к ограничению тока по амплитуде.
5.8. Индуктивная катушка под воздействием токов различной формы
На рис. 5.5, б приведена модель индуктивной катушки. Преобразуем эту модель, перейдя от последовательно соединенных индуктивности и сопротивления к параллельному соединению этих элементов. На рис. 5.15 показаны модель индуктивной катушки и импульс тока входного воздействия. Элементы модели связаны соотношениями:
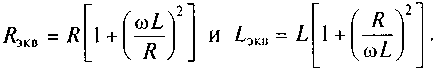
При частоте ω = 0 модуль комплексного сопротивления индуктивной катушки равен сопротивлению потерь R. С ростом частоты модуль ZL(ω) также растет и при частоте, определяемой выражением
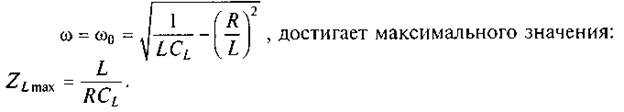
При частоте ω > ω0 активное сопротивление индуктивной катушки Rстановится существенно меньше реактивного сопротивления xl= ωL. Кроме того, ZL(ω)|ω>ω0=xc=1/(ωCL). Таким образом, при ω > ω0 сопротивление индуктивной катушки становится емкостным. Катушка теряет свои свойства индуктивности.
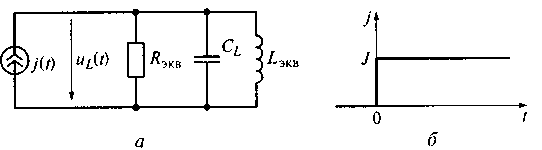
Рис. 5.15. Модель индуктивной катушки (а) и импульс
тока входного воздействия (б)
Допустим, что на индуктивную катушку воздействует импульс тока
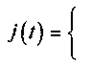 |
Jпри t ≥ 0;
0 при t < 0.
Учитывая количественную связь между коэффициентом затухания δ= 1/(RэквCL) и резонансной частотой ω0 = 1/√(LэквCL), временную зависимость напряжения на катушке можно описать тремя различными выражениями.
1. При равенстве коэффициента затухания и резонансной частоты δ=ω0 напряжение на индуктивной катушке имеет вид
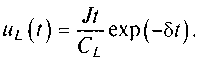
2. В случае, когда коэффициент затухания больше резонансной частоты (δ>ω0), напряжение на индуктивной катушке можно представить следующим образом:
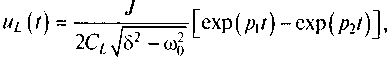
где p1=-δ+√(δ2-ω02) и p2=-δ-√(δ2-ω02).
3. Если коэффициент затухания меньше резонансной частоты (δ<ω0), то напряжение на индуктивной катушке описывается следующим выражением:
 (5.14)
(5.14)
В каждом из этих уравнений максимальная величина напряжения индуктивности ограничивается на уровне JR, где R — сопротивление потерь индуктивной катушки. Напряжение не стремится к бесконечности, как у идеализированной индуктивности. Таким образом, в индуктивной катушке часть энергии, подводимой к ней, рассеивается на сопротивлении потерь. Кроме того, согласно (5.14) индуктивная катушка способна излучать электромагнитные волны.
5.9. Добротность конденсатора и индуктивной катушки
В простейшем случае индуктивная катушка представляется последовательным соединением сопротивления потерь Rи индуктивности L. Это следует из условия, что для индуктивной катушки ωL»1/(ωС) в рабочем диапазоне частот. На рис. 5.16 показаны модель индуктивной катушки и диаграмма распределения комплексных токов и напряжений в ней.
Пусть через индуктивную катушку протекает ток i(t), изменяющийся по гармоническому закону i(t) = √2Icos(ωt+φ). Комплексная амплитуда тока имеет вид İ = √2 I ехр(jφ). Комплексное напряжение на внешних зажимах индуктивной катушки (см. рис. 5.16, б) описывается формулой
Ů = √2I ехр(jφ)(R + jωL) = √2I ехр(jφ) √(R2 +(ωL)2) exp[ jarctg(ωL/R)],
из которой следует, что при сопротивлении потерь индуктивной катушки, равном нулю
(R= 0), напряжение на ней опережает ток на угол ψ = π/2; [arctg(∞) = 90°]. При этом потери энергии в индуктивной катушке отсутствуют. При наличии же сопротивления потерь (R > 0) имеем ψ = arctg(ωL/R) < π2. Наличие дополнительного фазового сдвига в цепи
(ψ < π/2) говорит о наличии потерь энергии в индуктивной катушке.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.