Линейные цепи с сосредоточенными параметрами. Линейные четырехполюсники. Колебательные контуры (5-7 главы учебника "Радиотехнические цепи и сигналы" под ред. К.Е.Румянцева), страница 15

где с = 3 ·10⁸ м/с — скорость света в вакууме.

            Электрическая частота свободных колебаний в контуре связана с периодом, круговой частотой и длиной волны следующим соот­ношением:

f₀=ω₀/2π=1/T=c/λ₀=1/(2π√(LC)),

из которого следует, что параметры свободных колебаний в иде­альном контуре зависят только от параметров реактивных эле­ментов L и С.

7.2. Свободные колебания в контуре с потерями

Эквивалентная схема последовательного колебательного контура (рис. 7.2) состоит из индуктивности L, емкости С и активного сопро­тивления R= R_L+ R_c, которое равно сумме сопротивлений потерь индуктивной катушки R_Lи конденсатора R_c.

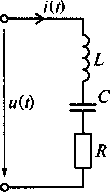
Рис. 7.2. Эквивалентная схема последовательного колебательного контура

             Наличие сопротивлений потерь приводит к тому, что свободные колебания в реальном и идеальном контурах при одинаковых L и С слабо отличаются по частоте и существенно отличаются по закону изменения амплитуды.

              При приложении к входным зажимам реального контура мгно­венного напряжения u(t) = Е_п происходит периодическое пре­образование энергии (электрической в магнитную и обратно), запасаемой в реактивных элементах L и С контура. Это преобразо­вание происходит на фоне потери энергии на активном сопро­тивлении R. Из-за этого амплитуда колебаний уменьшается во времени. Соответственно свободные колебания в реальном кон­туре носят затухающий характер. Изменение амплитуд колеба­ний I_m и U_mприводит к тому, что свободные колебания в конту­ре носят негармонический характер.

             Для проведения анализа колебательного процесса в реальном контуре уравнение (7.1) дополним слагаемым Ri(t), которое оп­ределяет падение напряжения на сопротивлении потерь. Тогда

L((di(t))/dt)+Ri(t)+(1/C)∫₀^ti(t)dt=E_n.

            Проанализируем работу контура при следующих трех соотно­шениях между коэффициентом затухания δ= R/2Lи круговой частотой свободных колебаний в контуре без потерь ω₀ = 1/√(LC).

           Случай 1. Соответствует условию  δ> ω₀, при котором

i(t)= (E_n/(2L√(δ²-ω₀²)))[ехр(-δt + √(δ²-ω₀²t)) - ехр(-δt - √(δ²-ω₀²t))].

           Случай 2. Предполагает, что δ = ω₀. Тогда

i(t)=(E_n/2L)t exp(-δt).

           Случай  3. При δ< ω₀, вводя понятие свободных колебаний в реальном контуре с потерями ω_св = √(ω₀² - δ²), находим

                                                  i(t)= I_m(t)sin(ω_свt).                                               (7.5)

            На рис. 7.3 показан колебательный процесс в контуре, имею­щем потери.

            В формуле (7.5) амплитуда сигнала (см. рис. 7.3)

                                                                                              (7.6)

не является постоянной величиной. Ее изменения определяются множителем exp(-δt), уменьшаясь от I_m(t = 0) = Е_п/(ω_свL) в мо­мент воздействия Е_п до нуля.

            Анализируя формулы (7.5) и (7.6), сформулируем основные свойства колебаний в реальном контуре.

    1.  Зависимость амплитуды свободных колебаний I_m(t) от вре­мени t подчиняется экспоненциальному закону (см. рис. 7.3).

            Амплитуда тока уменьшается в соответствии с постоянной вре­мени контура

τ₀ = 1/δ. При t = τ₀ амплитуда колебаний I_m(t) = I_m(0)/e = I_m(0)/2,718 = 0,37I_m(0).

            Таким образом, постоянная времени контура определяет вре­мя, в течение которого амплитуда свободных колебаний I_m(t) умень­шается на 63 % своего начального значения.

             За время от 0 до τ₀ амплитуда I_m(t)  уменьшится от I_m(0) до 0,37I_m(0). В интервале времени от τ₀ до 2τ₀ величина I_m(t)  умень­шится от 0,37I_m(0) до 0,14I_m(0) и т.д. Теоретически затухание коле­баний в реальном контуре происходит бесконечно долго. На практике переходной процесс можно считать законченным к моменту t=(4...5)τ₀. В этом случае амплитуда тока снижается на 95...99 % сво­его начального значения.

2.  Если бы контур был идеальным (R = 0), то его постоянная времени

 τ₀= 1/δ= 2L/Rстремилась бы к бесконечности. Колеба­тельный процесс в цепи был бы незатухающим и продолжался сколь угодно долго. С ростом R постоянная времени контура τ₀ уменьшается. При этом амплиту­да колебаний I_m(t) в контуре за­тухает быстрее.

             3.  В формулу для расчета час­тоты свободных колебаний реаль­ного контура ω_св входит сопро­тивление потерь R. Это говорит о влиянии активного сопротивле­ния контура на процесс обмена энергией между L и С. В то же время это влияние невелико и достаточно часто его можно не учитывать. Тогда                                         

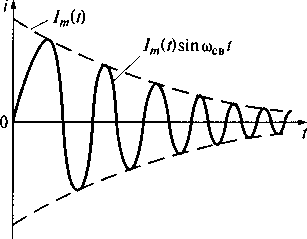
Рис. 7.3. Колебательный процесс в контуре с потерями

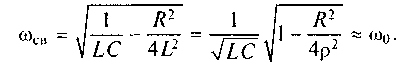                                                                    (7.7)

            На практике сопротивление Rисчисляется единицами и десят­ками Ом, а характеристическое сопротивление р — сотнями Ом. Поэтому в выражении (7.7) величиной R²/4p²можно пренебречь.

            4. Угол сдвига фазы между напряжением на индуктивной ка­тушке (конденсаторе) и током контура можно представить в виде

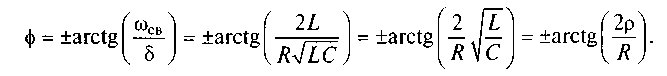
             В этом выражении отношение величин p/Rвелико, достигая сотен и тысяч. Это позволяет пренебречь влиянием сопротивле­ния потерь Rна фазовый сдвиг между напряжениями на элемен­тах и током в контуре и считать, что φ= ±arctg(∞) = ±90°. Таким образом, напряжение на емкости отстает от тока на угол в 90°, а на индуктивной катушке напряжение на угол в 90° опережает ток.

              5.  Колебательный процесс в реальном контуре возможен с ча­стотой свободных колебаний ω_св = √(ω₀² - δ²) , где ω₀>δ. Отсюда вы­текает и второе условие наличия колебаний в контуре R < 2р. Фи­зически это говорит о том, что потери в контуре, приобретая большую величину, препятствуют перезарядке конденсатора. Пе­реходной процесс в контуре подчиняется апериодическому зако­ну, и колебательный процесс в контуре отсутствует. На рис. 7.4 показана зависимость тока в контуре, имеющем потери, при R >p.

             6. Процесс затухания свободных колебаний в реальном контуре может быть охарактеризован добротностью Qконтура или затуха­нием d. Добротность контура определяется отношением энергии, запасаемой в контуре на реактивных элементах LI²_m/2, к мощ­ности, выделяемой на сопротивлении потерь, RI²_m/2 на частоте свободных колебаний, т.е.