Линейные цепи с сосредоточенными параметрами. Линейные четырехполюсники. Колебательные контуры (5-7 главы учебника "Радиотехнические цепи и сигналы" под ред. К.Е.Румянцева), страница 3

          Так, у ВАХ диода, расположенной в первом квадранте системы координат (прямая ветвь), сопротивление отточки к точке изменя­ется. Действительно, ток прямой ветви ВАХ диода описывается выра­жением i= Aехр(αu), где А и α — постоянные коэффициенты. Тогда сопротивление в каждой точке ВАХ можно представить в виде

                                              R=u/i=u/(Aexp(αu))=(u/A)exp(-αu).

           Из выражения видно, что с ростом напряжения сопротивле­ние диода уменьшается пропорционально экспоненте. Сопротив­ление обратной ветви ВАХ диода стре­мится к бесконечной величине из-за малых токов.

           Отличительной особенностью нели­нейных цепей является то, что на вы­ходе нелинейных цепей появляются гар­монические составляющие с частотами, которые отсутствуют во входном воз­действии. Например, при приложении к полупроводниковому диоду напря­жения u_вх(t) синусоидальной формы откликом будет ток i_вых(t), по форме представляющий только по­ложительные полуволны от полной синусоиды сигнала входного

воздействия. На рис. 5.3 показаны линеаризированная модель ВАХ i= f(u) и отклик i_вых(t)

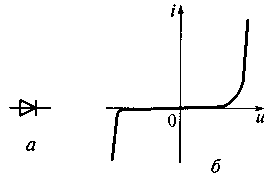
Рис. 5.2. Графическое обозна­чение (а) и ВАХ (б) полу­проводникового диода

 полупроводникового диода на входное гармоническое воздействие u_вх(t). Такая форма отклика включает множество гармонических составляющих, в частности постоян­ную составляющую, которая отсутствует в сигнале входного воз­действия. Входное напряжение изменяется по синусоидальному закону и, следовательно, средняя величина этого напряжения равна нулю.

          Нелинейные цепи не подчиняются принципу суперпозиции. Например, напряжения u₁ и u₂, приложенные поочередно к полу­проводниковому диоду, вызовут соответственно токи i₁ = Aехр(αu₁) и i₂ = Aехр(αu₂). Тогда суммарный ток, вызванный действием двух источников напряжения, i_сум= i₁ + i₂ = A[ехр(αu₁) + ехр(αu₂)]. При приложении же к диоду суммы напряжений u₁и u₂ получим ре­зультирующий ток i_рез= Aехр[α(u₁+u₂)] = Aехр(αu₁)ехр(αu₂).

           Из проведенных расчетов видно, что произведение двух экспо­нент exp(u₁)и ехр(u₂) больше суммы значений этих экспонент. Таким образом, принцип суперпозиции к нелинейным элемен­там не применим.

           Параметрическими цепями называют такие цепи, в которых параметр одного или нескольких элементов изменяется в соответ­ствии с заданным законом изменения внешнего управляющего напряжения. Как правило, параметры параметрических цепей из­меняются во времени.

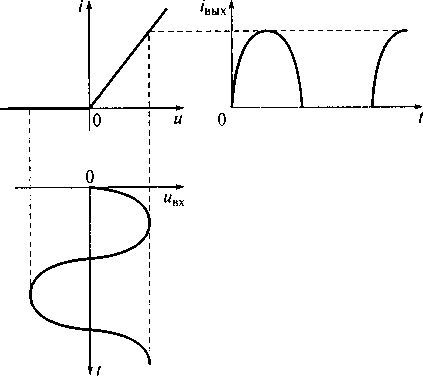
Рис. 5.3.Линеаризированная модель ВАХ i= f(u) и отклик i_вых(t) полупроводникового диода на входное гармоническое воздействие u_вх(t)

              Различают линейные и нелинейные параметрические цепи. В ли­нейной параметрической цепи параметр зависит от времени. В не­линейной параметрической цепи помимо зависимости парамет­ров от времени проявляется также зависимость некоторых пара­метров цепи от напряжения, тока и их направления в цепи.

              Пример 5.1. К резистору, сопротивление которого изменяется по за­кону

R = R ₀ /sin(ωt), приложено напряжение и = U₀sin(ωt). Необходимо  найти выражение, описывающее зависимость тока в этой параметричес­кой цепи.

              Решение. Ток в параметрической цепи согласно закону Ома имеет вид

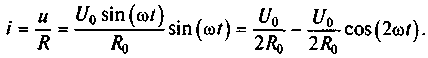
            Из выражения видно, что при приложении к заданному параметри­ческому резистору гармонического напряжения, изменяющегося с частотой ω, ток резистора будет содержать постоянную составляющую U₀/2R₀ и гармоническую составляющую (U₀/2Ro)cos(2ωt), изменяющуюся с удвоенной частотой 2ω.

            Рассмотрев различные виды радиотехнических цепей, можно сделать следующий вывод. Если в отклике цепи имеются гармони­ческие составляющие, которых нет во внешнем воздействии, то это говорит о наличии в цепи нелинейных и/или параметрических эле­ментов. В противном случае это будет линейная цепь.

5.2. Активные и пассивные линейные двухполюсники

           Линейные двухполюсники можно разделить на два класса: ак­тивные и пассивные.

           Активные двухполюсники. Активными двухполюсниками назы­вают источники электрической энергии, энергия которых образу­ется в генераторах напряжения и тока (рис. 5.4) путем преобразо­вания энергии другого вида (механической, химической, биохи­мической, световой и т.д.).

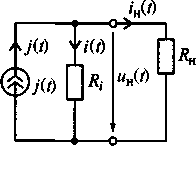
а                                 б

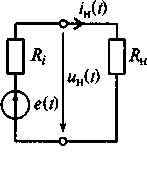
Рис. 5.4. Генераторы напряжения (а) и тока (б)

           Генератор напряжения состоит из идеализированного источни­ка напряжения e(t), амплитуда напряжения которого остается неизменной при изменении тока, потребляемого от источника, и внутреннего сопротивления R_i, включенного последовательно с источником напряжения.

          Генератор тока состоит из идеализированного источника тока j(t), амплитуда тока которого остается неизменной при измене­нии напряжения, приложенного к внешним зажимам источника тока, и внутреннего сопротивления R_i, включенного параллельно источнику тока.

          При отключении сопротивления нагрузки R_Hмощность, потреб­ляемая от генератора напряжения или тока, равна нулю (Р_н = 0), напряжение на внешних зажимах генератора напряжения равно ЭДС этого источника e(t), а напряжение на внешних зажимах ге­нератора тока и_н = R_ii(t).

           При подключении сопротивления нагрузки R_Hк внешним за­жимам генератора напряжения на внутреннем сопротивлении ис­точника R_iвозникает падение напряжения, вызванное током i_H(t), протекающим через R_Hи R_i. Из-за этого разность потенциалов на внешних зажимах источника будет меньше ЭДС генератора на­пряжения. Отсюда u_H(t) = e(t) - R_ii_H(t), где u_H(t) — напряжение, падающее на сопротивлении нагрузки; i_H(t) — ток, протекающий через нагрузку.

             При подключении сопротивления нагрузки R_Hк внешним за­жимам генератора тока ток i_H(t), протекающий через сопротивле­ние нагрузки R_H, не будет равен току источника j(t). Часть тока i_H(t)  = j(t)-u_H(t)/Rбудет замыкаться через внутреннее сопро­тивление R_iгенератора тока.