Конденсатор С может иметь как постоянную, так и переменную емкость. В первом случае колебательный контур будет настроен на несущую частоту одной радиостанции ωр = 1/√(LC). Во втором случае при изменении емкости конденсатора С можно перестроить резонансную частоту и настроить входную цепь приемника на требуемую радиостанцию.
В антенне наводятся ЭДС множества радиостанций, каждая из которых работает в своем частотном диапазоне и соответственно имеет свою частоту несущего колебания. Эти ЭДС на эквивалентной схеме (см. рис. 7.12, б) представлены генераторами напряжения e1 (ωpl), e2(ωp2), ..., еп(ωрn), внутренние сопротивления которых состоят из реактивной Хаи активной Rа составляющих выходного сопротивления антенны.
Емкость конденсатора либо индуктивность индуктивной катушки подбираются таким образом, чтобы настроить контур на несущую частоту ωр1 требуемой радиостанции. На этой частоте сопротивление контура равно сопротивлению потерь R, а коэффициент передачи напряжения имеет максимальное значение, равное добротности контура Q. Сигнал выбранной радиостанции усиливается в Qраз и поступает на вход последующего каскада. Для ЭДС других радиостанций контур расстроен, коэффициент передачи напряжения имеет малую величину (может быть даже меньше единицы). Таким образом, за счет избирательных свойств колебательного контура преимущественно усиливается сигнал выбранной радиостанции, а сигналы остальных радиостанций ослабляются, т.е. контур позволяет осуществить частотную избирательность.
Последовательный контур может быть использован для подавления колебаний, например помех, наводимых в антенне в определенном частотном диапазоне. Это можно осуществить, используя электрическую схему входной цепи приемника с фильтрующим элементом (рис. 7.13).
В этой цепи индуктивная катушка Lи конденсатор С позволяют настроить входную цепь приемника на несущую частоту требуемой радиостанции. Индуктивная катушка LФ, и конденсатор Сф образуют второй последовательный колебательный контур. На резонансной частоте сопротивление контура равно сопротивлению потерь, т.е. составляет по величине единицы или десятки Ом. Подобное сопротивление является шунтирующим между антенной и общей шиной («землей»), В результате этого первый колебательный контур закорачивается на резонансной частоте второго контура. Сигнал, соответствующий
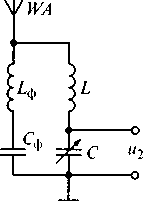
Рис. 7.13. Электрическая схема входной цепи приемника с фильтрующим элементом
этой частоте будет замыкаться на «землю» и не сможет пройти во входную цепь приемника. Это обеспечивает подавление помех во входных цепях приемника.
7.6. Параллельный колебательный контур основного вида
Параллельным колебательным контуром называется электрическая цепь, в которой имеются индуктивные и емкостные ветви включенные параллельно источнику энергии.
Эквивалентная схема параллельного колебательного контура основного вида (рис. 7.14) состоит из индуктивной катушки, представленной индуктивностью Lи сопротивлением потерь R, конденсатора, представленного емкостью С. Так как потери в конденсаторе пренебрежимо малы, то его сопротивление потерь не учитываем. Питается контур от источника энергии, например от генератора с большим внутренним сопротивлением Ri. Сопротивление нагрузки rh на эквивалентной схеме характеризует входное сопротивление последующего каскада, на который передается сигнал контура. Если контур питается от генератора напряжения, то амплитуда напряжения, снимаемого с контура, всегда меньше амплитуды напряжения генератора.
В целях анализа основных характеристик параллельного контура запишем выражение для расчета комплексного входного сопротивления:
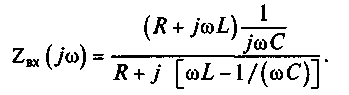 (7.12)
(7.12)
В условиях резонанса реактивные сопротивления индуктивной катушки ω0L и конденсатора 1/(ω0С) равны между собой. При этом реактивное сопротивление в знаменателе выражения (7.12) будет равно нулю. Найдем резонансную частоту контура
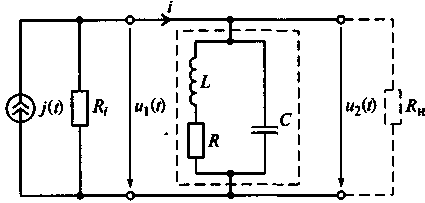
Рис. 7.14. Эквивалентная схема параллельного колебательного контура основного вида
ω0= 1/√LC , которая совпадает с резонансной частотой последовательного контура, составленного из тех же элементов, что и параллельный контур.
На частотах, близких к резонансной, реактивное сопротивление индуктивности ωL, существенно больше сопротивления потерь R. С учетом этого выражение (7.12) преобразуется к виду
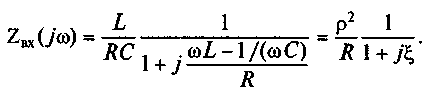
В показательной форме комплексное входное сопротивление параллельного колебательного контура имеет вид
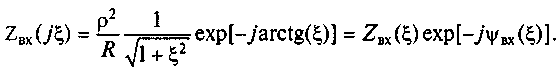
Модуль комплексного входного сопротивления контура и аргумент комплексного входного сопротивления контура определяются по формулам:
![]()
где R0 = p2/R — эквивалентное сопротивление контура на резонансной частоте.
На рис. 7.15 показаны модуль и аргумент входного сопротивления параллельного колебательного контура.
Рассматривая выражения для модуля и аргумента комплексного входного сопротивления параллельного контура, отметим следующие особенности (см. рис. 7.15).
1. На резонансной чистоте ω = ω0 модуль комплексного входного сопротивления контура достигает наибольшей величины R0 =p2/R. При увеличении индуктивности или уменьшении емкости контура модуль комплексного входного сопротивления растет пропорционально квадрату этих параметров. Уменьшение индуктивности и увеличение емкости контура приводят к снижению входного сопротивления контура.
2. При увеличении расстройки частоты модуль комплексного входного сопротивления контура снижается. При ξ= ±1 значение Zвх(ξ) уменьшается до уровня 0,707R0. В дальнейшем модуль сопротивления снижается более плавно.
3. При значениях обобщенной расстройки ξ = ±1 величина Zвх(ω) снижается до уровня 0,707. Это соответствует отклонению частоты от резонансной на величину
Δω1= ±ω0/(2Q). Значит, избирательности параллельного и последовательного контуров
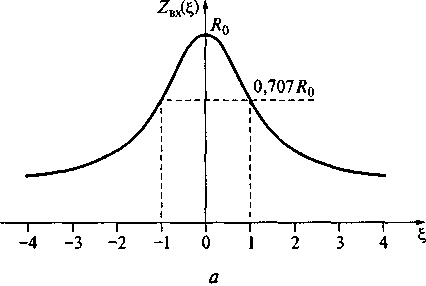
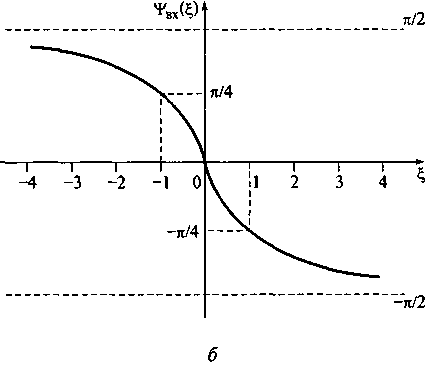
Рис. 7.15. Модуль (а) и аргумент (б) входного сопротивления
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.