В выражении (7.15) мнимая часть комплексного сопротивления на частоте резонанса токов равна нулю. С учетом этого можно записать ωpтL1 = 1/(ωртС) -ωpтL2. Подставляя полученное выражение в (7.15), находим входное сопротивление контура с разделенной индуктивностью на частоте резонанса токов:
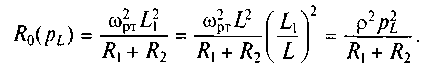
Таким образом, сопротивление контура с разделенной индуктивностью на частоте резонанса токов зависит от коэффициента включения индуктивности pL. Это позволяет, изменяя коэффициент включения pL, согласовать входное сопротивление контура с сопротивлением нагрузки или с внутренним сопротивлением источника тока, обеспечив наиболее эффективную работу контура.
На рис. 7.17 показаны модуль и аргументы входного сопротивления параллельного колебательного контура с разделенной индуктивностью.
Рассмотрим зависимость от частоты входного сопротивления контура с разделенной индуктивностью (см. рис. 7.17). В соответствии с (7.15) находим:
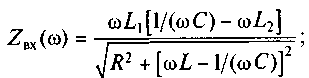(7.16)
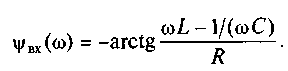(7.17)
В диапазоне частот ω< ωpт в (7.16) реактивное сопротивление емкости 1/(ωС) больше реактивных сопротивлений второй индуктивности ωL2 полной индуктивности ωL. С учетом этого в диапазоне частот 0<ω<ωpт комплексное входное сопротивление контура
определяется ветвью ωL1 и носит индуктивный характер. Модуль Zвх(ω)≈ ωL1 растет с ростом частоты. Аргумент комплексного входного сопротивления (7.17) при ω = 0 равен π/2. С увеличением частоты числитель в выражении (7.17) по модулю возрастает, аргумент уменьшается и при частоте ω = ωрт становится равным нулю.
Комплексное входное сопротивление контура при ω = ωрт является числом действительным R0 (pL), а аргумент равен нулю, поскольку в выражении (7.17) ωртL = 1/(ωртС).
При изменении частоты в диапазоне ωрт < ω < ωрн в числителе выражения (7.16) выполняется условие 1/(ωС) > ωL2, а в знаменателе этого выражения ωL > 1/(ωС) и
ωL > R. С учетом этого формула (7.16) сводится к виду
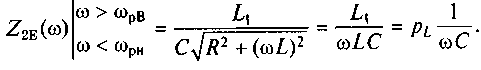
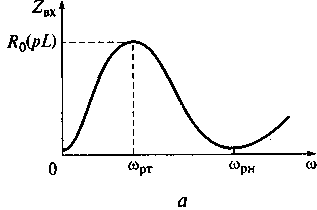
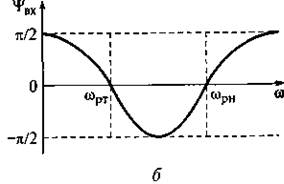
Рис. 7.17. Модуль (а) и аргумент (б) входного сопротивления параллельного
колебательного контура с разделенной индуктивностью
Полученное выражение позволяет в диапазоне частот ωрт < ω < ωрн выявить следующие два свойства параллельного колебательного контура с разделенной индуктивностью.
1. Входное сопротивление контура носит емкостный характер. С ростом частоты его модуль уменьшается. С учетом наличия в контуре сопротивления потерь R2можно записать, что при ω = ωрн справедливо приближение ZBX(ω) ≈ R2.
2. Аргумент входного сопротивления контура изменяется от 0 до -π/2, а при дальнейшем увеличении частоты — от -π/2 до 0. Достижение аргументом значения -π/2 объясняется тем, что величина входного сопротивления контура определяется параллельным соединением двух ветвей: L1 — R1 и L2— С— R2. Модуль входного сопротивления контура больше сопротивлений потерь в контуре R1 и R2.
При изменении частоты в диапазоне ω > ωрн комплексное входное сопротивление контура становится индуктивным, возрастая с увеличением частоты. В этом диапазоне частот аргумент возрастает от 0 до π/2.
Рассмотрим добротность параллельного колебательного контура с разделенной индуктивностью при частоте источника тока, равной частоте резонанса токов. В этом случае аргумент комплексного входного сопротивления контура равен нулю, т. е. ψвх(ωрт) = 0. Ток и напряжение на внешних зажимах контура будут определяться выражениями
i(t) = Imcos(ωpтt)
и
На частоте резонанса токов амплитудное значение тока Iml = Im2= Um/(ωpтL1) первой ветви, включающей индуктивность L1 и сопротивление потерь R1 равно амплитудному значению тока второй ветви из индуктивности L2, емкости С и сопротивления потерь R2. Однако эти токи отличаются по фазе на угол π. Напряжение емкости второй ветви ис отстает по фазе от тока на угол π/2. С учетом этого на частоте резонанса токов добротность контура с разделенной индуктивностью совпадает с добротностью последовательного и параллельного контуров основного вида, в которых L=Ll+L2.
Добротность параллельного колебательного контура с разделенной индуктивностью снижается при уменьшении сопротивления нагрузки. Подбирая коэффициент включения индуктивностей в соответствии с (7.14), можно согласовать сопротивление контура на частоте резонанса токов с сопротивлением нагрузки RH и подобрать требуемую эквивалентную добротность контура.
7.8. Параллельный колебательный контур с разделенной емкостью
Эквивалентная схема параллельного колебательного контура с разделенной емкостью приведена на рис. 7.18. Она включает одну ветвь, состоящую из конденсатора С1 и сопротивления потерь R1, и вторую ветвь, состоящую из конденсатора С2, индуктивной катушки Lи сопротивления потерь R2.
Основные характеристики параллельного колебательного контура с разделенной емкостью аналогичны характеристикам контура с разделенной индуктивностью и определяются следующими выражениями:
частота резонанса токов ωрт = 1/ √(LC);
характеристическое сопротивление контура р =√(L/С);
добротность контура Q = p/R.
Таким образом, частота резонанса токов, характеристическое сопротивление и добротность этого контура совпадают с соответствующими характеристиками, например, последовательного контура при условии, что С= C1 C2/(C1 + C2), а сопротивление потерь равно R = R1 + R2.
Частота резонанса напряжений контура ωрн = 1 /√( LC2) определяется параметрами элементов (С2, L) второй ветви контура.
Вводя понятие коэффициента включения емкости
pс=С/C1=C2/( С1 + С2 ),
находим частоту резонанса напряжений ωрн = ωрт √(1- рс).
Таким образом, частота резонанса напряжений ωрн в контуре с разделенной емкостью меньше частоты резонанса токов ω рт.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.