На рис. 2.11. Фаза колебаний в соседних резонаторах отличается на величину φ0
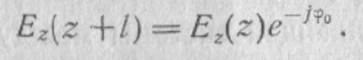
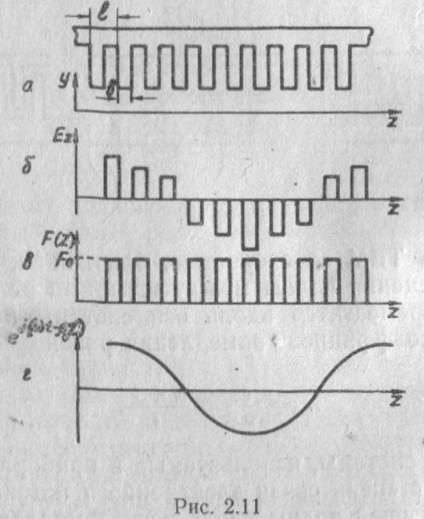
Электрическое поле сосредоточено вблизи щелей резонаторов. Поэтому зависимость продольной составляющей поля Ег от координаты г представляет собой серию импульсов с синусоидальной огибающей. Продольная составляющая поля (рис. 2.11,6) может быть представлена произведением двух функций
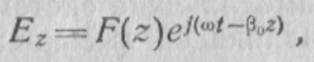 (2.1)
(2.1)
где
F(z) — периодическая последовательность импульсов одинаковой высоты с периодом I,
![]()
Периодическая в пространстве функция F{z) может быть разложена -в тригонометрический ряд
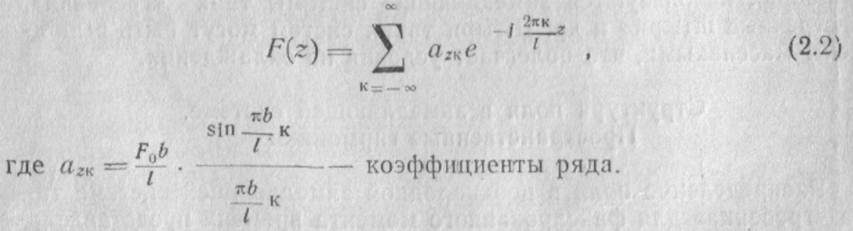
Если подставить (2.2) в (2.1), то получим выражение для поля в замедляющей системе в виде суммы гармонических бегущих волн
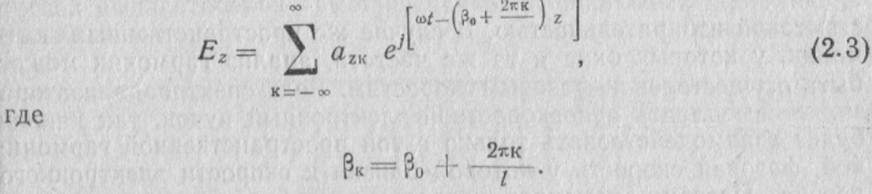
Выражение (2.3) показывает, что высокочастотное поле в замедляющей системе может рассматриватьсякак сумма бесконечного числа бегущих волн (пространственных гармоник) с постоянными распространения
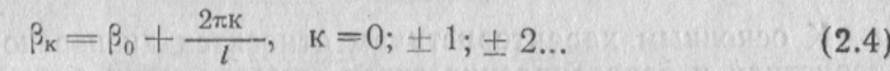
Фазовые скорости этих волн определяются соотношением
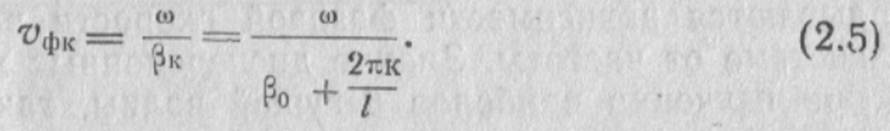
Пространственные гармоники, фазовые скорости которых положительны, т.е. совпадают по направлению с групповой скоростью, называются прямыми (положительными) гармониками. Если фазовая скорость отрицательная (направлена навстречу групповой скорости) — гармоники называются обратными (отрицательными).
Как следует из соотношения (2.5), с увеличением номера гармоник фазовая скорость уменьшается. Наибольшую фазовую скорость имеет основная гармоника (к=0).
Представление реально существующего поля в замедляющей системе суммой пространственных гармоник является одной из форм аналитического описания поля.
Пространственные гармоники существуют в замедляющей системе только одновременно. Каждая из гармоник, представляя элементарную гармоническую волну, не может удовлетворить периодическим граничным условиям. Только совокупность всех вместе взятых пространственных гармоник определяет полную картину результирующего поля.
Частота колебаний всех пространственных гармоник в силу линейного характера процессов в замедляющей системе одна и та же. Она равна частоте возбуждаемого ноля в замедляющей системе.
Всем пространственным гармоникам отвечает одна и та же групповая скорость, равная групповой скорости основной пространственной гармоники

Пространственные гармоники являются не менее очевидной физической реальностью, чем временные гармоники. В силу имеющегося различия по частоте у временных гармоник роль спектроанализаторавыполняетлинейная система —колебательный контур с высокой избирательностью. В случае же пространственных гармоник, у которых одна и та же частота, анализ гармоник может быть осуществлен по фазовым скоростям. Роль спектроанализатора может выполнить односкоростной электронный пучок, так как он будет взаимодействовать только с той пространственной гармоникой, фазовая скорость у которой близка к скорости электронного потока. Поэтому, изменяя скорость электронов, можно осуществить взаимодействие электронного потока с одной из пространственных гармоник.
Основные характеристики замедляющих систем
К основным характеристикам относятся дисперсионные характеристики и сопротивлениесвязи замедляющих систем.
Дисперсионными характеристиками замедляющих систем называются зависимости фазовой скорости волны в замедляющей системе от частоты. Знание дисперсионных характеристик важно при изучении приборов бегущей волны, так как позволяет установить полосу пропускания, возможность взаимодействия электронного потока с прямыми и обратными гармониками, значение скоростей электронов для обеспечения высокой эффективности взаимодействия поля и потока, возможности электронной перестройки автогенератора и настройки усилителя.
Поэтому расчет дисперсионных характеристик является оченьважной задачей при изучении свойств замедляющих систем.
Для расчета дисперсионных характеристик применяются электродинамические методы, основанные на использовании уравнении Максвелла, и метод эквивалентных схем. Для целого ряда замедляющих систем, таких, как «встречные штыри», спираль, которыешироко используются в приборах бегущей волны, решение уравнений электродинамическими методами затруднено. В этом случае широкое распространение получил метод эквивалентных схем. Этот метод основан на замене отдельных участков и элементов замедляющих систем некоторыми эквивалентными сосредоточенными индуктивности ми и емкостями, что в значительной меры позволяет упростить расчеты. Одновременно оказывается возможным сохранить достаточную для практики точность при определении дисперсии.
Замедляющая система типа «гребенка» и ее эквивалентная схема изображены на рис. 2.12.
Выбор эквивалентной схемы зависит от физических свойств замещаемой замедляющей системы. Гребенчатую замедляющую систему можно представить цепочкой контуров (LC) с емкостной связью (С1). Собственными потерями в замедляющей системе пренебрегают, т. с. считают все параметры эквивалентных схем реактивными. Иногда параметры эквивалентных схем удается рассчитать, а в большинстве случаев эквивалентные схемы составляют на основании физических соображений о картине полей в замедляющей системе с последующей экспериментальной проверкой.
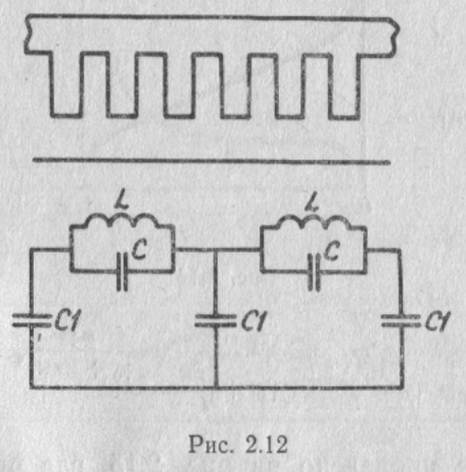
Эквивалентная схема рассматриваемой замедляющей системы является цепочкой фильтров нижних частот.
Для построения дисперсионных характеристик цепочки фильтров используют хорошо разработанную теорию линейных электрических схем с сосредоточенными параметрами. Как известно из теории фильтров, фазовый сдвиг на каждую ячейку эквивалентной схемы, представленной на рис. 2.12, изменяется в пределах от 0 до π (рис. 2.13). Зная зависимость фазового угла от частоты, можно построить дисперсионную характеристику замедляющей системы для основной волны (рис. 2.14)
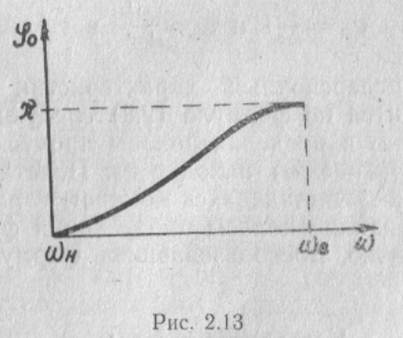

По дисперсионной характеристике основной волны могут быть построены дисперсионные характеристики всех других пространственных гармоник, если воспользоваться соотношением (2.5)
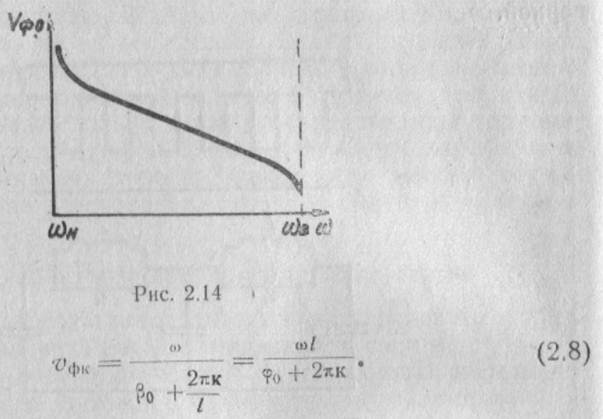
Такое построение проведено на рис. 2.15, где представлены дисперсионные характеристики основной волны (к=0) и пространственные гармоники (к≠0). Дисперсионная характеристика основной волны располагается выше прямой
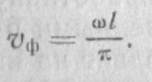
Аналогично дисперсионные характеристики первой прямой пространственной гармоники располагаются между прямыми
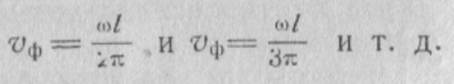
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.