Замедляющие системы. Генераторы с электрическим управлением электронным потоком. Методы и устройства стабилизации частоты и фазы колебании в задающих генераторах простых и сложных сигналов, страница 4

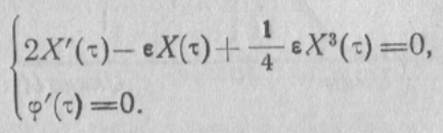
Решение уравнений представляется в виде

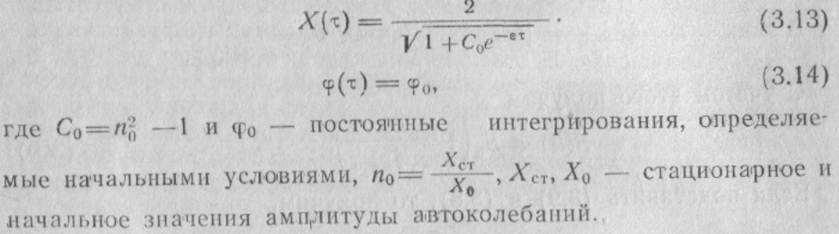
Обсуждение решения уравнений

1. Колебания нарастают, если X₀<X_ст ,  ε>0, т. е. при условии K’S₀ R_э >1.

Поскольку S₀=S_макс, то дли обеспечении самовозбуждения ав­тогенератора необходимо подбирать требуемую величину коэффициента обратной связи изменением взаимного положения контур­ной катушки и катушки обратной связи и величину R₃.

2. Амплитуда колебаний Х(τ) нарастает по закону, близкому к экспоненциальному (рис. 3.3).

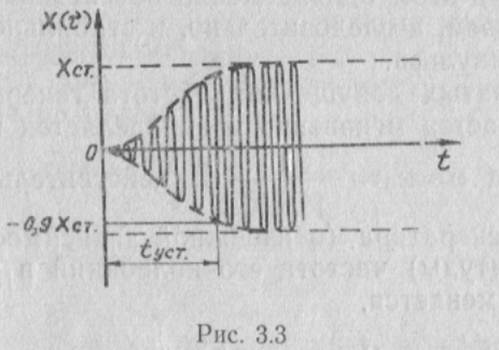
3. Время установления амплитуды колебаний зависит от на­чальных условии, параметров автогенератора и режима его рабо­ты. Если считать процесс установления амплитуды закончившим­ся при X(τ) =0,9Х_ст, то из (3.13) получим

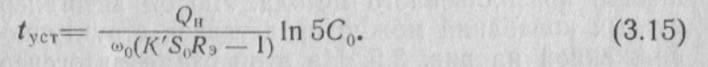
В основном время установления зависит от добротности колебательной системы Q_н, частоты генерации ω₀ и начальных условий

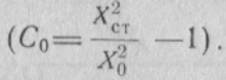
Зависимость времени установления амплитуды колебании от начальных условии представлена на рис. 3.4. Как следует из графиков, время установления существенно зависит от начального значения амплитуды и уменьшается с ее увеличением.

4. Стационарная амплитуда не зависит от начальных условий. При τ→∞Х_ст→2. Стационарная амплитуда полностью определя­ется параметрами генератора.

5.  Начальная фаза колебаний определяется начальными усло­виями и не зависит от времени. Это указывает   на   возможность фазирования автогенераторов внешним   сигналом.   Это   явление широко используется на практике для фазирования   когерентных гетеродинов. При этом одновременно обеспечивается   постоянство начальных условий, а следовательно, и стабильность длительности фронта радиоимпульса.

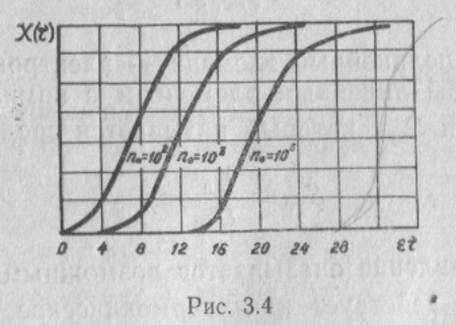
6.  При принятых допущениях частота генерируемых   колеба­ний устанавливается мгновенно и определяется параметрами контура генератора

В действительности в силу неизохронности генератора (неизбежной зависимости частоты коле­баний от амплитуды) частота его колебаний в процессе установ­ления также изменяется.

Квазилинейный метод

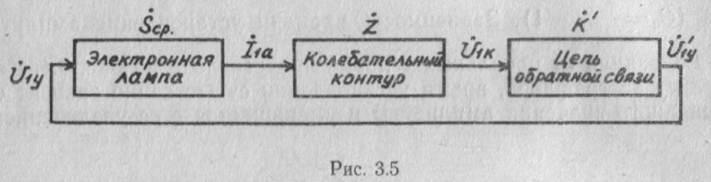
Использование метода медленно меняющихся амплитуд позво­лило изучить процесс установления колебаний в автогенераторе. При изучении установившихся колебании используется квазили­нейный метод, предложенный Ю. Б. Кобзаревым. Рассмотрим су­щество квазилинейного метода. Любой автогенератор высокочас­тотных колебаний можно представить структурной схемой, изо­браженной на рис. 3.5. На этой схеме автогенератор изображен последовательным включением трех четырехполюсников: нелиней­ного безынерционного и двух линейных.

Существенно нелинейный элемент — электронная лампа пред­ставляется как бы линейным элементом с комплексным коэффи­циентом передачи S_q, , который называется средней крутизной

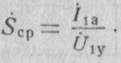
Такое представление оказывается возможным в силу того, что на входе лампы действует квазигармоническое напряжение U_1y снимаемое с колебательного контура. Анодный ток лампы является существенно негармоническим и содержит основную (первую) и высшие гармонические составляющие, зависящие от напряже­ния U_1y .Но вследствие высокой фильтрующей способности колебательного контура (Q_{н >>} 1) высшими гармониками можно пре­небречь и учитывать только первую гармонику анодного тока.

Таким образом, токи и напряжения в генераторе оказываются гармоническими функциями времени и для анализа амплитудных и фазовых соотношений в стационарном режиме можно использо­вать метод комплексных амплитуд.

Коэффициенты передачи колебательного контура и цепи обрат­ной связи соответственно равны

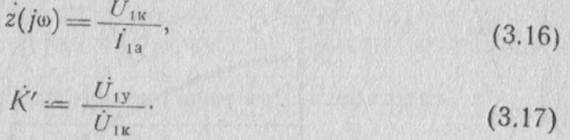
Для стационарного режима произведение   коэффициентов пе­редачи четырехполюсников равно единице U’_1y = U_1y

Коэффициенты передачи элементов генератора   можно   запи­сать следующим образом:

Уравнение (3.22) получило название условия баланса амплитуд, а (3.23) — условия баланса фаз в автогенераторе.

В условии баланса амплитуд средняя крутизна является функцией амплитуды колебаний генератора. Если рабочая точка лампы выбрана на линейном участке характеристики, то сростом амплитуды колебаний в генераторе средняя крутизна уменьшает­ся (рис. 3.6,а). Поскольку R’_э   К’ практически не зависят от амплитуды U_1y, зависимость 1\K’ R_э  представляет линию, па­раллельную абсцисс. Абсцисса точки пересечения этом линии с кривой S_cp(U_1y) и определяет стационарную амплитуду U_1y  (ст),

 

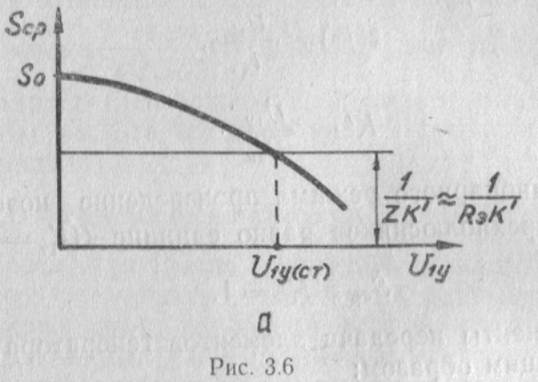
Легко показать, что автогенератор устойчив по амплитуде. Увеличение или уменьшение  амплитуды управляющего напряжении вызывает уменьшение или увеличение S_ср, что способствует возвра­щению амплитуды колебаний автогенератора   к   стационарному

состоянию.

Уравнение (3.23) является условием баланса фаз.

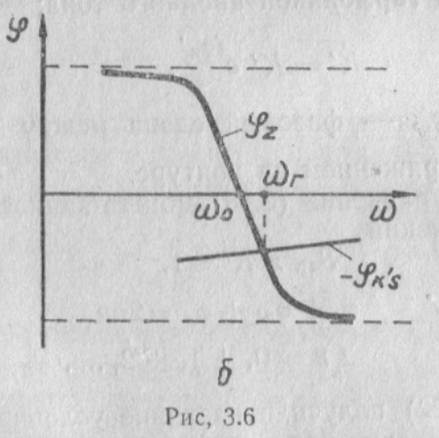
Графическое решение уравнения баланса фаз для определения частоты генерируемых колебаний представлено на рисунке (3.6,б). Фазовый угол φ_z существенно зависит от частоты. Для параллельного резонансного контура зависимость φ_z (ω)определяется выражением

жительные направления токов и напряжений на схеме показаны стрелками):

Таким образом, фазовые условия будут выполняться в том слу­чае, если реактивные сопротивления Х_ск и Х_акна   резонансном

частоте имеют один и тот же характер,   а  третье  сопротивление Х_ас противоположный им, что следует из (3.24).

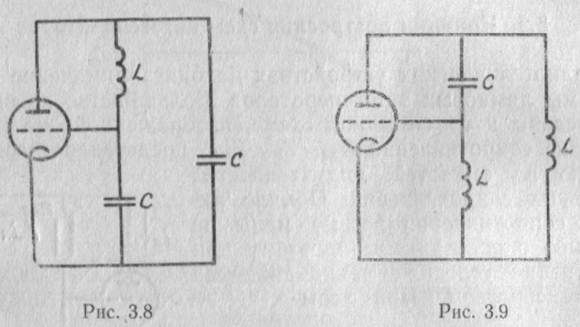
Автогенератор, в котором Х_ск и Х_асносят емкостной характер, а Х_ас— индуктивный (.рис. 3.8), называют емкостной трехточкой. Если в схеме Х_ас и Х_ск— индуктивности, а Х_ас — емкость, то схема называется индуктивной трехточкой (рис. 3.9).

Практические схемы одноконтурных автогенераторов

В схеме автогенератора должна быть обеспечена возможность подачи постоянных напряжений и прохождения по цепям постоян­ной и переменной составляющей токов.

Должна быть предусмотрена цепь положительной обратной связи и возможность настройки генератора на оптимальный ре­жим (регулировка частоты ω, коэффициента обратной связи К и коэффициента связи с нагрузкой, от которого зависит величи­на R_э

Колебательная система автогенератора может состоять из од­ного или нескольких контуров. В зависимости от количества кон­туров автогенераторы называются двух- или трехконтурными. Та­кие колебательные системы обладают двумя или тремя собствен­ными частотами.