Чтобы получить количественную оценку результата усиления сигнала в клистроне, необходимо последовательно рассмотреть процессы модуляции электронного потока по скорости в зазоре первого резонатора, затем процесс образования сгустков электронов в пространстве дрейфа и, наконец, возбуждение в улавливателе колебаний с частотой входного сигнала.
На рис. 4.2, б схематично показан входной резонатор клистрона и структура электрического поля в зазоре в некоторый момент времени. Если принять, что входные СВЧ колебания представляют гармонический процесс, то в первом приближении напряженность поля сигнала в области взаимодействия с электронным потоком изменяется до закону
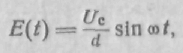
где d — длина зазора группирователя.
Сила, действующая на электрон в электрическом поле, определяется известным соотношением: F=ma=eE, где е — заряд электрона. Представляет интерес выражение для скорости электрона, прошедшего резонатор. Для этого последние уравнения может представить в следующем виде:
![]()
Если принять, что электрон, движущийся с
начальной скоростью, в момент![]() подходит к резонатору, а в момент времени
подходит к резонатору, а в момент времени ![]() выходит из него со
скоростью
выходит из него со
скоростью ![]() , то,
разделяя переменные в последнем уравнении, его решение нетрудно найти по
следующей формуле:
, то,
разделяя переменные в последнем уравнении, его решение нетрудно найти по
следующей формуле:
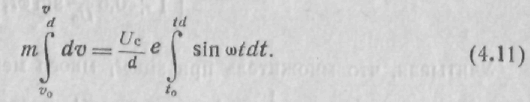
В результате интегрирования выражение для скорости электрона приобретает вид
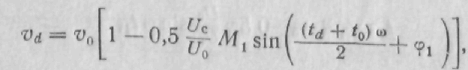
![]()
где М1 и ![]() -величины, зависящие от времени пролета электрона. При высокой начальной
скорости
-величины, зависящие от времени пролета электрона. При высокой начальной
скорости ![]() и малой длине зазора резонатора
и малой длине зазора резонатора
![]() можно
в первом приближении не учитывать это время.
можно
в первом приближении не учитывать это время.
Обозначая время пролета электроном
средины зазора резонатора, равное![]() , через
, через![]() , можно получить оценочное выражение для
искомой величины
, можно получить оценочное выражение для
искомой величины![]() :
:
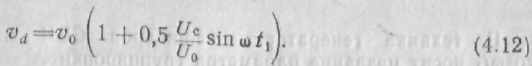
нетрудно заметить, что электроны, прошедшие область группирователя, изменяют свою скорость в зависимости от фазы СВЧ поля в зазоре резонатора, и электронный поток получает модуляцию по скорости с частотой усиливаемого сигнала.
Для оценки процесса перехода модуляции электронного потока по скорости в модуляцию по плотности необходимо найти выражение для конвекционного тока в клистроне на некотором удалении от группирователя в произвольном сечении вдоль оси z (рис. 4.2,а).
Для
группирователя электронный поток практически однороден по плотности. Если
группа электронов за время в плоскости зазора резонатора ![]() переносит заряд
переносит заряд ![]() , то эта же группа электронов,
проходя в пространстве дрейфа сечение z
, то эта же группа электронов,
проходя в пространстве дрейфа сечение z
за время ![]() переносит заряд
переносит заряд ![]() . В силу закона сохранения заряда
. В силу закона сохранения заряда ![]() и тогда
и тогда
![]()
искомое значение тока можно найти из уравнения
Время прохождения электроном
плоскости![]() зависит от его скорости и равно
зависит от его скорости и равно
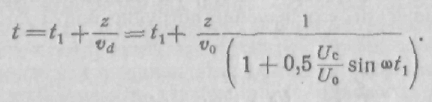
Учитывая, что
множитель при ![]() много меньше единицы, а
также соотношение
много меньше единицы, а
также соотношение![]() , последнее уравнение
, последнее уравнение
можно представить в следующем виде:
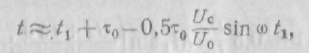
После вычисления dt/dt1 и подстановки в уравнение искомое значение конвекционного тока равно
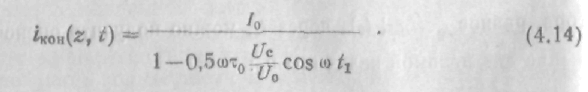
В
технике генераторных приборов СВЧ множитель при ![]() носит название параметра группировки
X
носит название параметра группировки
X
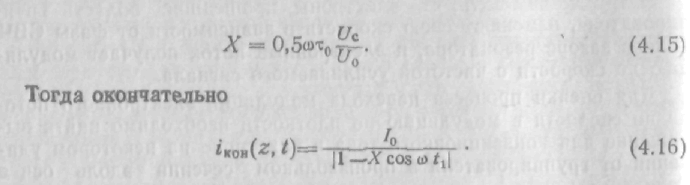
Анализ
последнего уравнения свидетельствует о следующем. Поскольку параметр
группировки зависит![]()
то существует
такое расстояние от группирователя, где![]() ".
В этом сечении электронные сгустки, следующие с частотой, будут иметь
максимальную плотность (при
".
В этом сечении электронные сгустки, следующие с частотой, будут иметь
максимальную плотность (при ![]() значение
значение ![]() ),
и в этой области целесообразно размещать резонатор-улавливатель.
),
и в этой области целесообразно размещать резонатор-улавливатель.
Наконец,
необходимо провести оценку значения наведенного тока в улавливателе,
расположенном в фиксированном сечении![]() .
.
Поскольку конвекционный ток представляет
периодический процесс с частотой ![]() , его можно
представить суммой ряда Фурье относительно момента времени
, его можно
представить суммой ряда Фурье относительно момента времени![]() в следующем виде:
в следующем виде:
Полученный
интеграл можно привести к табличному![]() , выраженному
функцией Бесссля первого рода
, выраженному
функцией Бесссля первого рода![]() порядка от
аргумента
порядка от
аргумента![]() :
:
![]()
Если теперь
воспользоваться уравнением для ![]() , то для
, то для
амплитуд гармонических составляющих конвекционного тока можно получить следующую зависимость:
![]()
Представленное выше выражение для конвекционного тока дает возможность из уравнения (разд. 2) найти соотношение для наведенного тока
![]()
где![]() — момент прохождения электронами
зазора второго резонатора;
— момент прохождения электронами
зазора второго резонатора;
![]() — величины, зависящие от времени
пролета электроном зазора второго резонатора, которые, в первом приближении,
можно принять равными 1 и 0 соответственно.
— величины, зависящие от времени
пролета электроном зазора второго резонатора, которые, в первом приближении,
можно принять равными 1 и 0 соответственно.
Поскольку
резонатор-улавливатель настроен на частоту какой-либо из гармоник, то в нем
возникнут колебания соответствующей частоты. Если клистрон выполняет лишь
функции усилителя, то выходной резонатор настраивается на первую гармонику и
амплитуда усиленных колебаний равна![]() —эквивалентное сопротивление
резонатора для первой гармоники тока, а
—эквивалентное сопротивление
резонатора для первой гармоники тока, а ![]() определяется
уравнением для наведенного тока:
определяется
уравнением для наведенного тока:![]()
Мощность высокочастотных колебаний,
выделяемая в выходном резонаторе, определяется известным равенством:![]()
![]() ,
и тогда коэффициент полезного действия клистрона можно найти из равенства
,
и тогда коэффициент полезного действия клистрона можно найти из равенства
![]()
Повышение КПД требует увеличения амплитуды колебаний в резонаторе, что, в первую очередь, связано с необходимостью обеспечения в нем хорошей добротности. Последнее же приводит К сужению полосы пропускания усилителя на клистроне.
Коэффициент
полезного действия клистрона зависит также от отношения ![]() ,
которое, в соответствии с (4.18), можно аналитически оценить, используя графики
функции Бесселя. Графики этой функции для
,
которое, в соответствии с (4.18), можно аналитически оценить, используя графики
функции Бесселя. Графики этой функции для ![]() приведены
на рис. 4.3.
приведены
на рис. 4.3.
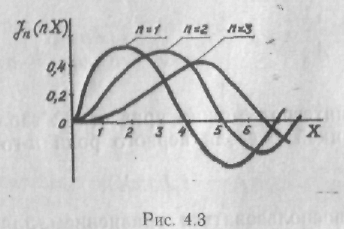
Оптимальный
параметр группировки ![]() соответствует значению
1,84, что обеспечивает
соответствует значению
1,84, что обеспечивает ![]() . Очевидно, что
отношение
. Очевидно, что
отношение![]() } в (4.20)
не может быть больше единицы, ибо при
} в (4.20)
не может быть больше единицы, ибо при ![]() электроны
в зазоре выходного резонатора будут не толь ко тормозиться, но и двигаться в
обратном направлении, нарушая работу клистрона. Поэтому при оценке нужно
принять, что
электроны
в зазоре выходного резонатора будут не толь ко тормозиться, но и двигаться в
обратном направлении, нарушая работу клистрона. Поэтому при оценке нужно
принять, что ![]() заметно меньше единицы и не следует
ожидать высокого значения КПД в двухрезонаторном клистроне. Практически он не
превышает 15%, Невелик и коэффициент усиления мощности, достигающий величины не
более 20 дБ.
заметно меньше единицы и не следует
ожидать высокого значения КПД в двухрезонаторном клистроне. Практически он не
превышает 15%, Невелик и коэффициент усиления мощности, достигающий величины не
более 20 дБ.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.