Замедляющие системы. Генераторы с электрическим управлением электронным потоком. Методы и устройства стабилизации частоты и фазы колебании в задающих генераторах простых и сложных сигналов, страница 28

Кроме перечисленных, в некоторых генераторных приборах не­обходимо учитывать и другие виды шумов: в ЛПД — шум лавин­ного умножения носителей; в биполярных транзисторах — шум токораспределения, связанный со случайным распределением то­ка 'между электродами; в диодах Ганна — доменные шумы или тепловые шумы «горячих» электронов.

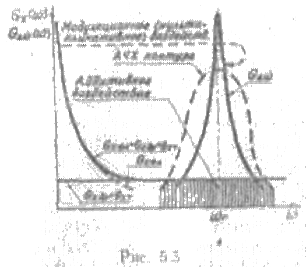
Механизм воздействия естественных дестабилизирующих фак­торов показан на рис. 5.5. Высокочастотные составляющие   шу­мов, попадающие в (полосу пропускания  колебательной  системы, складываются с ВЧ ко­лебанием, то есть воздействуют аддитивно   (заштрихован­ная область на рис. 5.5). Помимо   аддитивного   влияния, шумы в элементах схемы ав­тогенератора оказывают также мультипликативное модуляционное воздействие на час­тоту      автоколебаний (см. рис. 5.5). При этом основное влияние оказывают низкочастотные составляющие шумов. Низкочастотные составляющие шумов непосредственно не попадают в полосу пропускания контура и цепи обратной связи. Тем колебательной системой, как видно из выражения (5.11), она рав­на

Выражение (5.13) указывает общие пути реализации методов параметрической стабилизации частоты автогенератора:

использование элементов с малой чувствительностью к деста­билизирующим факторам — должны быть малыми);

увеличение фиксирующей способности   автогенератора  или хотя бы одно слагаемое должны быть большими; уменьшение дестабилизирующих факторов

Применительно к автогенератору с резонансной колебательной системой (рис. 5.5) конкретные пути повышения стабильности частоты колебании вытекают из выражения (5.11).

Полученные результаты поясняются графически на пример лампового автогенератора. Графическое решение уравнения баланса фаз для случая, когда Aip,  ни имеет место смещение резонансной частоты контура  приведено на рис. 5.7. Из рисунка видно, что при этом отклонение   частоты   колебаний    автогенератора    равно  .

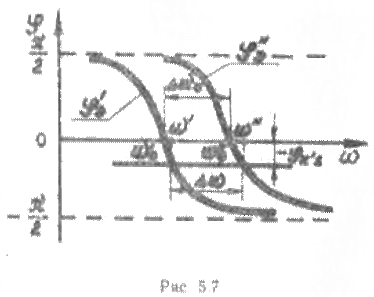
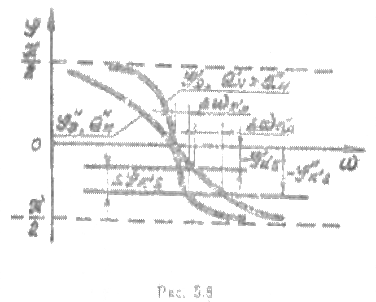
На рис. 5.8 приведены аналогичные графики для двух значений нагруженной добротности контура при условии, что оно имеет место изменение фазового угла равно  . что величина отклонения частоты колебаний автогенератора при увеличении  становится меньше. И наконец на рис. 5.9 приведены графики для двух значений при условии, что а величина изменения фазового угла в обоих случаях одинакова:  Видно, что величина отклонения частоты колебаний автогенератора при одинаковой величине тем больше, чем больше угол

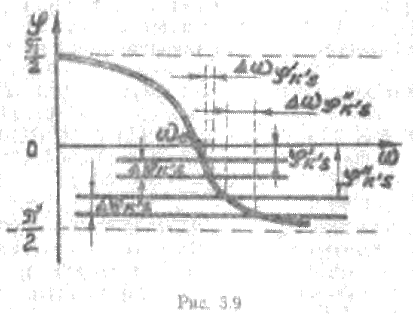
не менее их влияние на стабильность частоты автоколебаний, как правило, является определяющим. Эти случайные флуктуации, возникающие в элементах схемы автогенератора, приводят к флуктуациям активных и реактивных параметров этих элементов емкости С, индуктивности L крутизны характеристики S и внут­реннего сопротивления R генераторного прибора и др. , а сле­довательно, к шумовой модуляции токов и напряжений в этих элементах. Это обусловливает случайную модуляцию анодного тока автогенератора. Возникающие при этом флуктуации фазы первой гармоники анодного тока эквивалентны флуктуациям фазового угла ф которые, как видно из выражения (5.7), приводят к флуктуациям частоты автоколебаний.

5.2.3. Связь между нестабильностями электрических параметров и частотой колебаний автогенератора

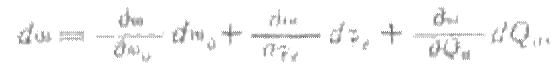
Выполнив дифференцирование, получим

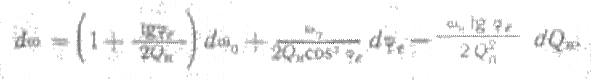
Для расчета относительного изменения частоты найдем пол­ный дифференциал выражения (5.10) для частоты колебаний ав­тогенератора как функции трех переменных.

Последним членом этого выражения и вторым слагаемым в скобках можно пренебречь ввиду их малости. Учитывая это и пе­реходя от дифференциалов к конечным приращениям, найдем относительное изменение частоты

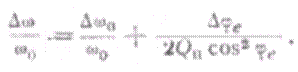 (5.11)

Полученное выражение является одним из основных соотно­шений теории стабилизации частоты. Оно показывает, что для обеспечении высокой стабильности частоты необходимо:

Обеспечить стабильность собственной частоты   колебательной системы генератора , то есть высокую эталонность   колебательной системы.

Обеспечить максимальную величину нагруженной   доброт­ности колебательной системы поскольку, Чем выше   доброт­ность, тем меньше влияют на частоту любые изменения фазового угла электронной проводимости.

Обеспечить работу генератора с малым значением  при
котором .

В общем случае любой автогенератор может быть представ­лен замкнутой цепью из  элементов (рис. 5.6). Условие существования

стационарных периодических колебании в такой системе может быть записано в виде

где к, и  — модуль и фазовый угол комплексного   коэффици­ента передачи j-го элемента.

Частота автоколебаний определяется из условия баланса фаз

где к = 0,1,2  

Каждый из фазовых углов  является функцией частоты  дестабилизирующих факторов. Тогда, если пренебречь пе­реходными процессами, полный дифференциал суммы фазовых уг­лов будет равен

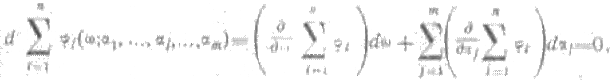
После деления правой и левой частей полученного уравнения на  и его решения относительно  с последующим переходом от дифференциалов к конечным малым приращениям получим

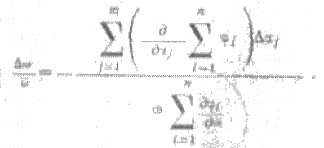(5.13)

Выражение, стоящее ,в знаменателе, называется фиксирующей, способностью автогенератора. Для автогенератора с резонансной.

5.3. Методы стабилизации частоты колебаний автогенераторов

5.3.1. Классификация методов стабилизации частоты

Методы стабилизации частоты колебаний автогенераторов мо­жно разделить на две группы:

методы параметрической стабилизации;

методы синхронизации и автоподстройки.

Мерная группа относится к прямым методам, преследующим цель устранить или уменьшить дестабилизирюущие факторы. Вто­рая группа относится к косвенным методам, предусматривающим уменьшение нестабильности частоты, не изменяя величины деста­билизирующих факторов.

Выбор метода стабилизации зависит от диапазона частот авто­генератора, его назначения, требуемой стабильности частоты, ре жима работы, условий эксплуатации, допустимых себестоимости и стоимости эксплуатации, ряда других факторов. Рассмотрим в начале сущность параметрических методов стабилизации ча­стоты.

5.3 2. Методы параметрической стабилизации частоты