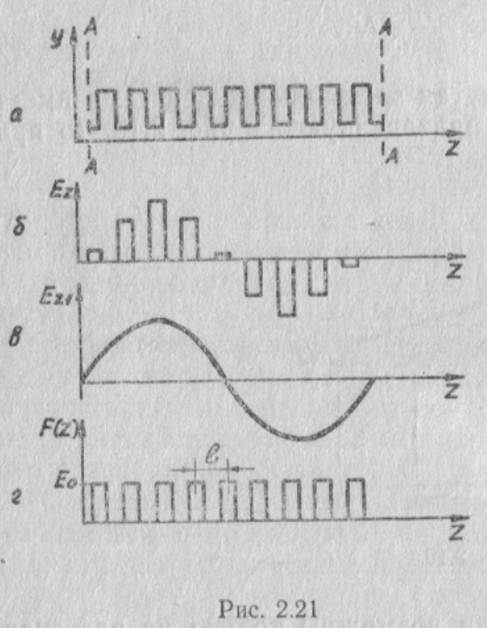
Проведем расчет поля в замкнутой замедляющей системе, для чего режем кольцевую замедляющую систему в сечении A (рис. 2.20,a) и развернем ее вдоль оси г (рис. 2.21,а).
В замкнутой в кольцо замедляющей системе продольная составляющая электрического поля (рте. 1.21,6) описывается выражением
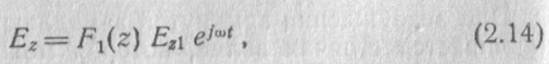
где F1(z) — периодическая последовательность импульсов с периодом l;
![]()
Дополним определение функций Ez1и F1 (z) для значений от - ∞ до ∞, продолжив их в обе стороны по оси г. Разложим F1 (z) в ряд Фурье Ez1 представим формулой Эйлера. В результате получим
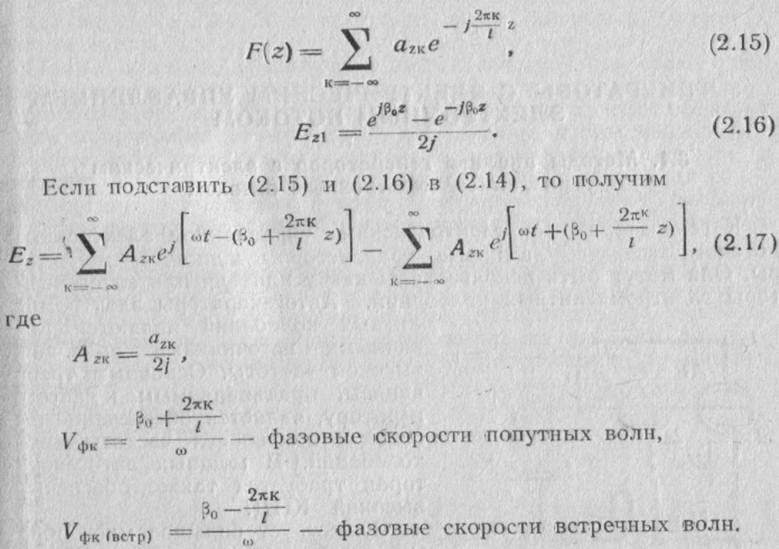
Таким образом, в замкнутой замедляющей системе каждой пространственной гармонике попутной волны будет соответствовать пространственная гармоника встречной волны, сдвинутая относительно попутной по фазе на 180°, так что пары этих гармоник образуют стоячие волны пространственных гармоник, которые в сумме составляют стоячую волну результирующего поля.
3 ГЕНЕРАТОРЫ С ЭЛЕКТРИЧЕСКИМ УПРАВЛЕНИЕМ ЭЛЕКТРОННЫМ ПОТОКОМ
3.1. Методы анализа генераторов с электрическим управлением электронным потоком
К генераторам с электрическим управлением электронным потоком относятся ламповые, транзисторные и диодные генераторы. Они могу быть использованы как усилители или автогенераторы электромагнитных колебаний. Автогенераторы электромагнитных колебаний являются первичными источниками колебаний высокой частоты. Основным требованием, предъявляемым к автогенератору, является обеспечение высокой стабильности частоты авто колебаний. В мощных автогенераторах требуется также обеспечить высокий КПД.
Существует большое многообразие схем автогенераторов. Однако вследствие общности физически: процессов, протекающих в автогенераторах, они описываются похожими дифференциальными уравнениями. Поэтому изучение автогенераторов с электрическим управлением рассмотрим на примере лампового генератора с трансформаторной обратной связью (рис.3.1).
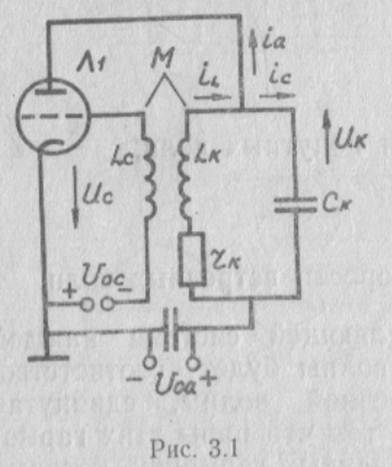
Ламповый автогенератор включает электронную лампу (Л1), колебательный контур (LK, CK, rк), цепь положительной обратной связи (Lc) и источник питания (С0а). Колебания в автогенераторе возникают самопроизвольно при малейших нарушениях электрического равновесия в результате включении источников питания, флуктуации электрического токав цепях генератора, обусловленных шумами. Эти флуктуации благодаря наличию обратной связи между анодной и сеточной цепями вызывают изменение напряжения на управляющей сетке, которое, в свою очередь, так изменяет анодный ток, что он поддерживает возникшие флуктуации. Режим работы генератора и параметры элементов генератора подбираются так, что колебания возникают и начинают нарастать со сколь угодно малых амплитуд. Нарастание колебаний не может быть беспредельным. Установление стационарной амплитуды обусловлено нелинейностью характеристики лампы. В установившемся режиме вся энергия, доставляемая в контур первой гармоникой анодного тока, идет на компенсацию активных потерь с учетом нагрузки.
Таким образом, колебания в автогенераторе нарастают при выполнении двух условий:
подаваемое из колебательной системы через цепь обратной связи напряжение должно иметь такую фазу, чтобы вызываемое им изменение тока лампы приводило к пополнению энергии в контуре;
энергия, доставляемая в контур первой гармоникой анодного тока за период колебаний, должна превышать потери в контуре за то же время.
Первое условие составляет физический смысл так называемого условия баланса фаз, а второе условие - баланса амплитуд.
Для составления уравнения автогенератора воспользуемся законами Киргофа. Для схемы, приведенной на рис. 3.1, получим два уравнения, связывающие токи и напряжения в анодном контуре,
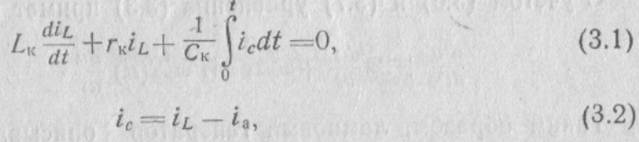
где гк — активное сопротивление, учитывающее потери в контуре.
Подставим выражение (3.2) в (3.1), затем в целях более удобного перехода в полученном уравнении от токов к напряжениям 'дважды продифференцируем последнее по t. В результате получим
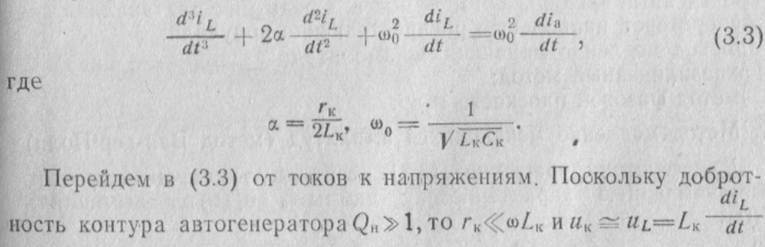

Таким образом, ламповый генератор описывается нелинейным дифференциальным уравнением второго порядка. Нелинейность уравнения обусловлена нелинейной зависимостью крутизны характеристики лампы от управляющего напряжения и.
Общие методы решения нелинейных дифференциальных уравнений второго порядка и выше пока не разработаны. Поэтому при решении уравнения используют приближенные методы, имеющие определенные границы применимости. Среди них для анализа автогенераторов наибольшее распространение получили:
метод медленно меняющихся амплитуд;
квазилинейный метод;
метод фазовой плоскости и др.
Метод медленно меняющихся амплитуд (метод Ван-дер-Поля)
Для решения уравнения (3.8) необходимо аппроксимировать вольт-амперную характеристику лампы ia,= f(u) и вычислить S(u).
Наиболее приемлемой является аппроксимация степенным полиномом вида
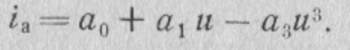
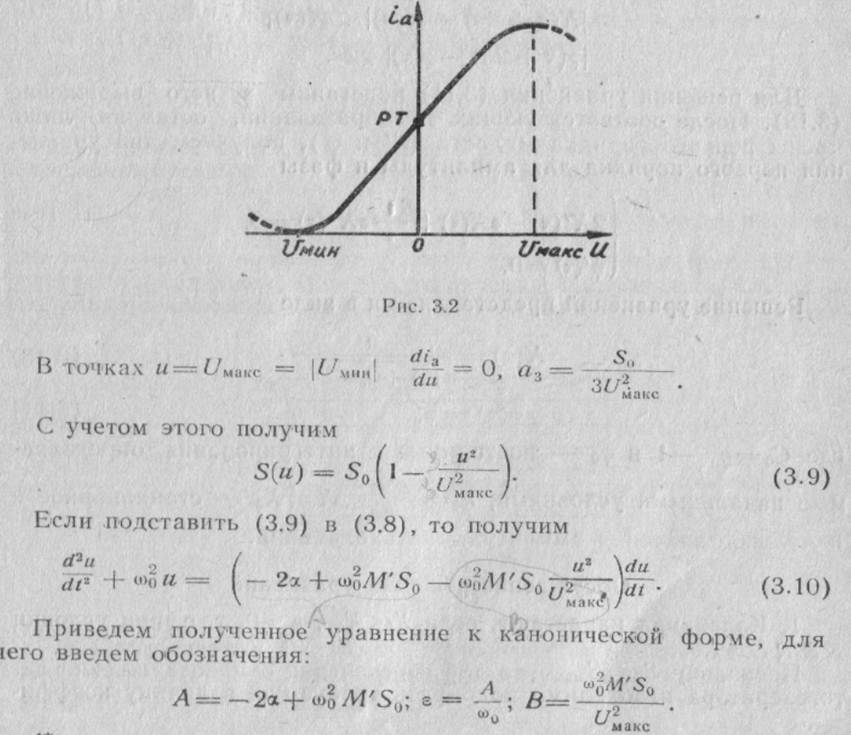
Эта зависимость имеет локальные максимум Uмакс и минимум Uмин .Она хорошо совпадает с реальной зависимостью iа(u) только в пределах участка между экстремальными точками. Поэтому используемая аппроксимация пригодна для исследования такого режима работы автогенератора, при котором управляющее напряжение и незначительно выходит за пределы этого участка.
Вычисляем
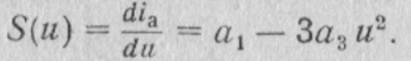
Для расчета коэффициентов а1 иа3 воспользуемся характерными точками кривой рис. 3.2. В точке U=0 S(U)=S0= а1.
Кроме того, введем
«безразмерные» напряжение ![]() и время τ= ω0 t
и время τ= ω0 t
После выполнения необходимых преобразований поручим уравнение, называемое уравнением Ван-дер-Поля:
![]()
Вследствие того, что добротность колебательной системы генератора велика (Qk >>1)- колебания носят квазигармонический характер. Изменения амплитуды и фазы колебаний от периода к периоду незначительны, Поэтому решение ищут в виде квазигармонического колебания
![]()
где Х(τ) и φ(τ) — «медленно» меняющиеся амплитуда и фаза колебания.
Условия «медленности» выражаются неравенствами:
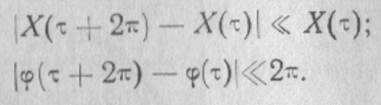
Для решения уравнения (3.11) подставим в него выражение (3.12). После соответствующих преобразований, оставляя лишь члены первого порядка малости {X' и φ'), получаем два уравнения первого порядка для амплитуды и фазы
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.