Замедляющие системы. Генераторы с электрическим управлением электронным потоком. Методы и устройства стабилизации частоты и фазы колебании в задающих генераторах простых и сложных сигналов, страница 2

Построение дисперсионных характеристик пространственных гармоник проводится по формуле (2.8) следующим образом. За­даются значения ώ в пределах полосы пропускания и по извест­ной зависимости φ₀=φ(ώ) находят φ₀. Подставляют значения φ и ώ в формулу (2.8) и, задаваясь номером гармоники к, вычисля­ют υ_{фк .}На границе полосы пропускания фильтра групповая скорость равна пулю. Воспользовавшись формулой Рэлея

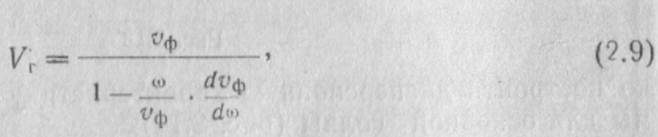
замечаем, что на границе полосы пропускании касательные к дис­персионным характеристикам являются вертикальными линиями.

По знаку фазовой скорости основной волны замедляющие сис­темы подразделяются на замедляющие системы прямой волны и замедляющие системы обратной волны. У замедляющих   систем

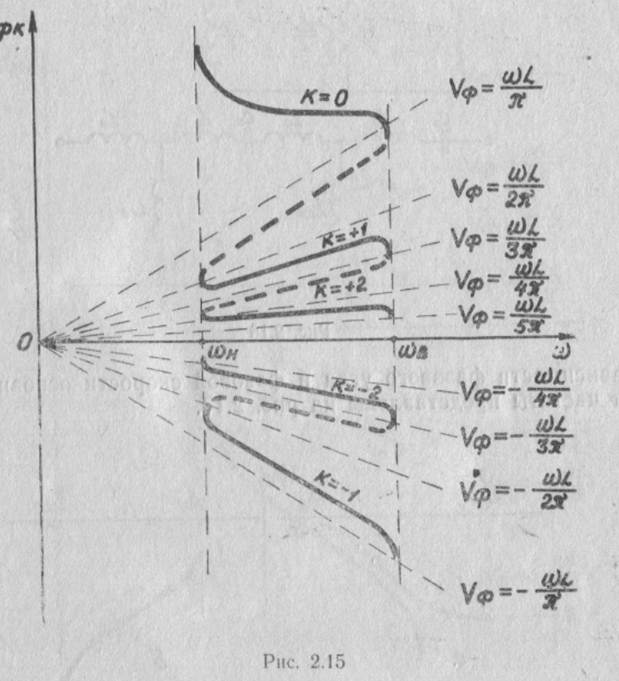
прямой полны фазовая скорость основной волны положительная, у обратной волны — отрицательная.

Гребенчатая замедляющая система относится к замедляющим системам прямой волны. Наряду с гребенчатой к замедляющим  системам прямой волны относятся спираль, цепочка резонаторов типа «щель-отверстие» и др. Гребенчатая замедляющая система со связками (рис. 2.10,г), пеночка связанных резонаторов (рис. 2.10,д) и «встречные штыри» {рис. 2.10,е) относится к за­медляющим системам обратной волны.

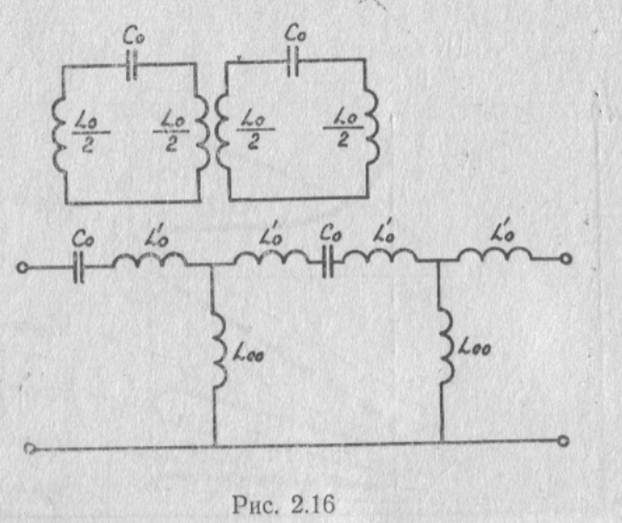
Эквивалентные схемы резонатором, связанных петлями (рис. 2.10,д), изображены на рис. 2.16.

Эквивалентная схема замедляющей системы цепочки   резонаторов, связанных петлями, представляет цепочку фильтров верх­них частот. Как известно из теории фильтров, фазовый сдвиг на каждую ячейку эквивалентной схемы, представленной на рис. 2.16, изменяется в пределах от — π до 0.

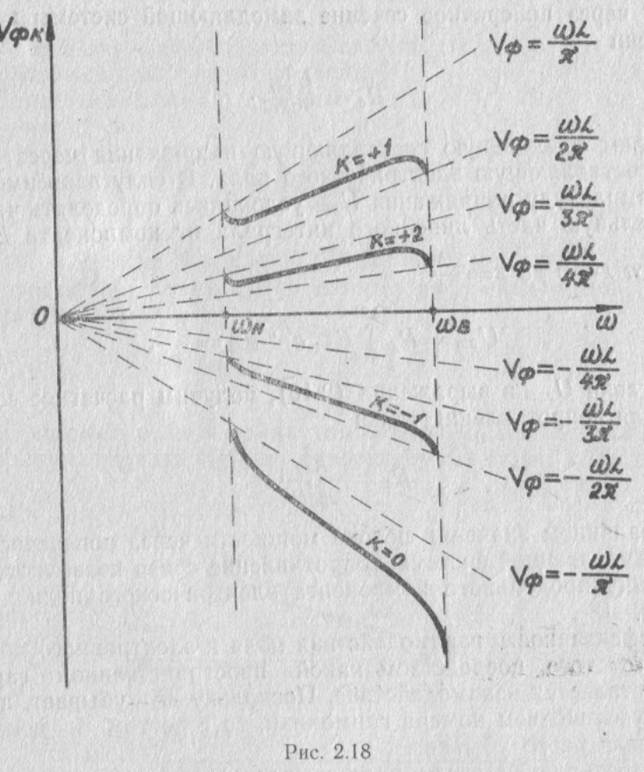
Зависимости фазового угла и фазовой скорости основной волны от частоты представлены на рис. 2.17.

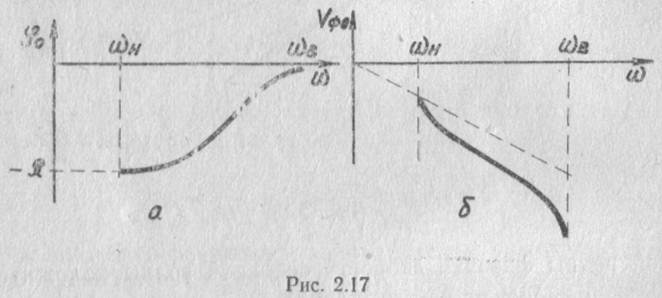
Как и для замедляющей системы прямой волны, воспользовав­шись соотношением

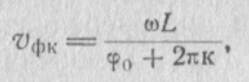
можно построить дисперсионные характеристики всех простран­ственных гармоник (рис. 2.18). Фазовая скорость основной волны является отрицательной, поэтому система связанных петлями резонаторов является замедляющей системой обратной волны.

В приборах бегущей волны используются оба типа замедляю­щих систем. Однако в приборах прямой волны преимущественно используются замедляющие системы прямой полны, а в приборах обратной волны — замедляющие системы обратной волны. Это обусловлено тем, что взаимодействиеэлектронного потока обыч­но осуществляется с основной волной, продольная составляющая

электрического поля которой имеет наибольшую интенсивность. А поскольку в приборах прямой полны электронный поток вза­имодействует с прямой гармоникой, а в приборах обратной волны — с обратной, то в качестве взаимодействующих гармоник выбираются основные волны.   

Сопротивление связи замедляющих систем

В приборах бегущей волны усиление СВЧ колебаний происходит в результате взаимодействия поля замедленной волны с потоком электронов.

Для количественной оценки эффективности взаимодействия продольной составляющей электрического поля с потоком элек­тронов вводится параметр замедляющей системы R_С, называемый сопротивлением связи. По аналогии с длинными линиями сопро­тивление связи замедляющей системы определяется отношением квадрата амплитуды продольного напряжения U_zm соответствую­щей пространственной гармоники к потоку мощности, проходя­щему через поперечное сечение замедляющей системы вединицу времени

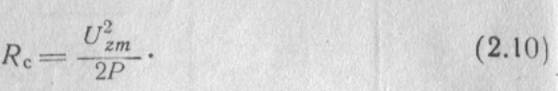
Выразим продольную составляющую напряжения через продольную составляющую электрического поля. В силу зависимости Е_zk от zамплитуду напряжения U_zmусловились определять через действительную часть линейного интеграла от компонента Е_zkвзятого от z=0 до z=Λ\4.

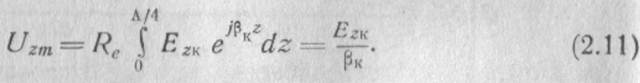
Подставив U_zmв выражение (2.10), получим расчетное соотношение для сопротивления связи

При заданном значении потока мощности через поперечное сече­ние замедляющей системы сопротивление связи позволяет оценить величину продольного компонента электрического поля бегущей волны.

Эффективность взаимодействия поля и электронного потока за висит от того, посредством какой   пространственной   гармоники осуществляется взаимодействие. Поскольку Е_zk убывает, а β_k рас­тет с увеличением номера гармоники, то с ростом   к   сопротивление связи резко убывает.

Сопротивление связи рассчитывается либо у поверхности за­медляющей системы, либо на оси симметрии, как например для спирали, где пропускается электронный поток. С удалением от поверхности замедляющей системы продольная составляющая поля Е_zk убывает, а следовательно, убывает и сопротивление связи.

2.2.3. Замедляющие системы, замкнутые в кольцо

При замыкании :в кольцо замедляющей системы она приобрета­ет резонансные свойства, что позволяет развивать в зазорах боль­шую амплитуду высокочастотного поля на нескольких фиксированных частотах.

Это вызвано тем, что в замкнутой замедляющей системе мо­гут существовать колебания только тех частот, для которых вдоль замедляющей системы укладывается целое число воли, что экви­валентно фазовому сдвигу вдоль замкнутой замедляющей систе­мы, равному целому числу 2π, т. е.

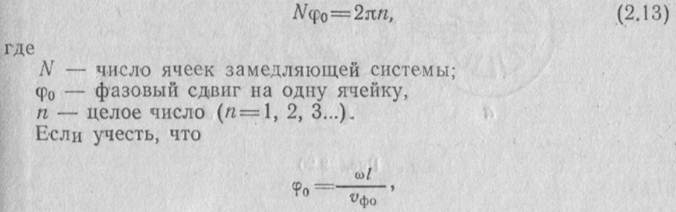
то воспользовавшись   условием   (2.13), находим зависимость фа зоной скорости U_фо от номера п, которая выражается следующим соотношением:

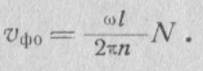
Таким образом, если разомкнутая замедляющая система имеет дисперсионную характеристику, приведенную на рис. 2.19, то при

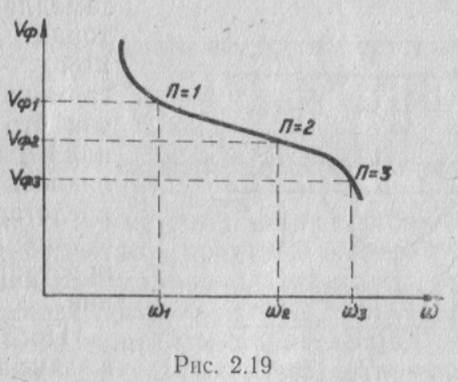
замыкании ее в кольцо колебания возможны только на частотах ω₁ , ω₂ , ω₃ …., соответствующих целым значениям п.

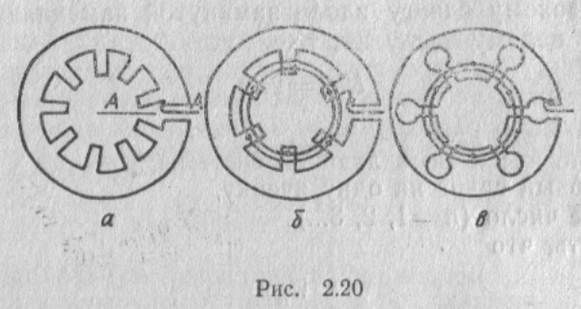
Форма резонаторов, цепочка которых образует замкнутую в  кольцо замедляющую систему, может быть самой разнообразной  (гребенка, гребенка со связками, «щель-отверстие» со связка­ми  и др. (рис. 2.20)).

При возбуждении замкнутой замедляющей системы в ней устанавливается стоячая волна, которая может быть представлена в виде двух движущихся навстречу друг другу бегущих волн с разными амплитудами.

Если в разомкнутой неоднородной замедляющей системе ре­зультирующее поле можно представить суммой бегущих волн, называемых   пространственными гармониками, то, по-видимому,   в замкнутой в кольцо замедляющей системе   результирующее преставится  суммой   бесконечного числа попутных пространственных гармо­ник, как и в разомкнутой замедляющей системе, ко­торая   дополняется суммой пространственных гармоник встречных волн, так что  результирующее поле в замкнутой замед­ляющей системе можно представить бесконечной суммой стоячих волн всех пространственных гармоник.