Учебно-методический комплекс по дисциплине «Теоретические основы автоматизированного управления», страница 60

Управлять состоянием системы x(t) можно изменением вектора входа u(t), а наблюдать ее состояние можно, измеряя вектор выхода y(t). В связи с этим возникают два вопроса, имеющих кардинальное значение для теории автоматического управления.

Можно ли, выбрав соответствующим образом входы u(t), перевести объект управления из некоторого произвольного состояния x(t_o) в другое произвольное состояние x(t₁)?

Можно ли, наблюдая вектор выхода y(t) в течение достаточно долгого промежутка времени, определить начальное состояние объекта x(t_o)?

Ответ на первый вопрос связан с понятием "управляемость", а ответ на второй вопрос - с понятием "наблюдаемость".

Определение понятий "управляемость" и "наблюдаемость". Понятие "управляемость" связано с возможностью приведения системы в заданное состояние с помощью входных или управляющих воздействий.

Понятие "наблюдаемость" связано с возможностью определения переменных состояния по результатам измерения выходных переменных.

В качестве примера, поясняющего эти понятия, рассмотрим объект (рис. 5.8), описываемый уравнениями состояния:

Из рисунка 5.8 видно, что переменная х₁ не соединена с входом u и поэтому он не может влиять на ее изменение во времени. Такую переменную состояния называют неуправляемой. Переменная х₂ не соединена с выходом и поэтому по наблюдению выхода y невозможно определить х₂. Такую переменную состояния называют ненаблюдаемой.

Более общее определение управляемости заключается в следующем.

Состояние[x_o, t_o] называют управляемым, если можно найти момент времени t₁  (t₁ > t_o) и вход u(t), переводящий систему за интервал времени [t_o, t₁] из состояния [x_o, t_o] в состояние [0, t₁]. Если любое состояние х ÎХ является управляемым для t_o, то объект называют полностью управляемым в момент времени t_o. Если объект полностью управляем в указанном выше смысле для любого t_o, то его называют полностью управляемым.

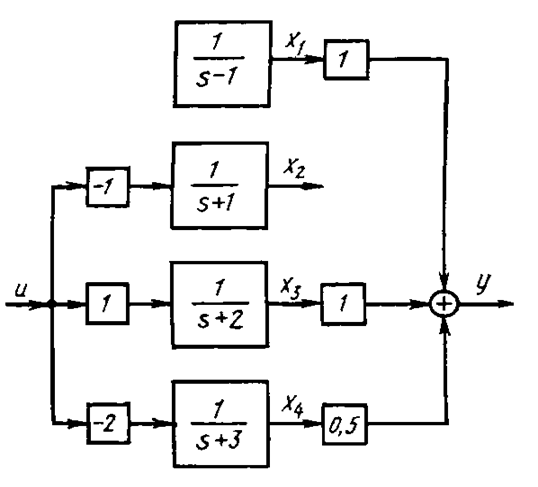
Рис. 5.8.

Можно также дать следующее определение.

Систему называют полностью управляемой, если для любых моментов времени t_o и t₁, t₁ > t_o и любых заданных состояний х_о и х₁ существует управление u(t), (t_o < t < t₁), переводящее начальное состояние х_о в конечное х₁.

Судить о том, является ли система управляемой по виду ее уравнений состояния в общем случае (за исключением примера одномерной системы), очень трудно.

Однако, для САУ, которая имеет в пространстве состояний линейную модель

американским ученым Р. Калманом получено необходимое и достаточное условие управляемости.

Необходимое и достаточное условие для управляемости системы (5.13) заключается в том, чтобы матрица

имела ранг n.

Часто матрица (5.14) имеет ранг n для некоторого v < n, т. е.

Наименьшее значение v, при котором имеет место равенство (5.15), называют показателем  управляемости.

Из выражения (5.14) видно, что управляемость определяется свойствами матриц Аи В. Критерий управляемости (5.14) остается справедливым и для дискретной системы, если ее уравнения представить в виде

x_k+1 = Ax_k + Bu_k.

Как было показано в рассмотренном выше примере, переменная х₂ является ненаблюдаемой, если она не соединена с выходом и по наблюдению выхода y ее определить невозможно. Но для управления необходимо располагать сведениями о текущих значениях вектора состояния. Поэтому возникает вопрос: при каких условиях, наблюдая векторы выхода и входа, можно найти переменные состояния х?

Систему (5.13) называют наблюдаемой, если по данным измерения или наблюдения векторов y(t) и u(t) на конечном интервале времени t_o £ t £ t₁ можно однозначно определить начальное состояние x(t_o). Систему (5.13) называют полностью наблюдаемой, если наблюдаемы все состояния в любые моменты времени.

Предполагая, что уравнения системы приведены к нормальной форме, рассмотрим уравнение связи между вектором выхода y и вектором состояния x: