Учебно-методический комплекс по дисциплине «Теоретические основы автоматизированного управления», страница 50

Применение этого же преобразования к импульсу, сдвинутому на kT₀, дает

.

С учетом этих соотношений уравнение (3.8) приобретает вид

.

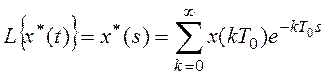Отсюда следует, что преобразование Лапласа дискретной функции времени является периодической функцией с частотой повторения w₀ = 2p/T₀.

Для точного восстановления непрерывного сигнала по последовательности его дискретных значений необходимо, чтобы частота квантования w₀ удовлетворяла условию теоремы Котельникова

w₀³ 2w_max .

Следовательно, для такта квантования Т₀должно выполняться условие

T₀ £p/w_max.

Заметим, что в системах управления или передачи информации на практике непрерывные сигналы с ограниченными спектрами не встречаются. Тем не менее, в теории цифрового управления частота

w_Sh = w₀/2 = p/T₀

играет роль своего рода эталонной константы. Она определяет полосу пропускания дискретной системы.

Фиксирующий элемент. Если в дискретной системе после квантователя стоит фиксатор (экстраполятор нулевого порядка), который на период, равный такту квантования, фиксирует мгновенное значение дискретного сигнала x(kT₀), на его выходе формируется ступенчатый сигнал (рис. 3.8).

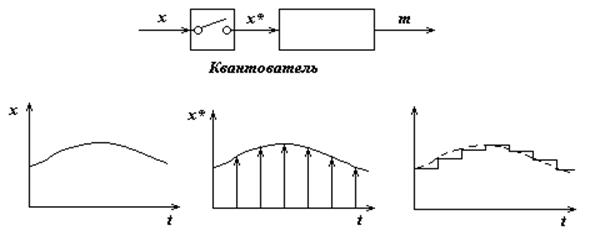
Рис. 3.8.

Передаточную функцию экстраполятора нулевого порядка можно получить следующим образом. Предположим, на вход его поступает последовательность импульсов

.

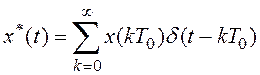Выходом экстраполятора является ступенчатый сигнал

.

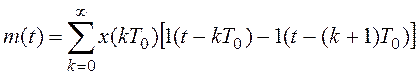Выполнив преобразование Лапласа, получаем передаточную функцию экстраполятора нулевого порядка:

На низких частотах он ведет себя подобно фильтру с передаточной функцией апериодического звена:

.

3.4. Введениев z-преобразованиедискретных сигналов

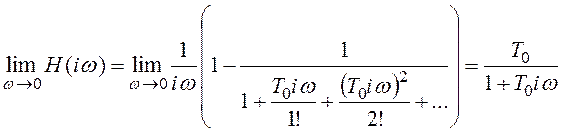Определив новую переменную

подставим ее в уравнение (3.9). В результате получаем z-преобразование импульсного сигнала x^*(t):

Этот бесконечный ряд сходится, если все его члены êx(kT₀)êограничены и если справедливо условие êzê>1. Поскольку величина s может выбираться произвольно, сходимость имеет место для широкого класса функций x(kT₀). Следует иметь в виду, что метод  z-преобразования основывается на тех же предположениях, что и преобразование Лапласа, причем особенно важно выполнение условия x(kT₀) при k <0.

Приведенные в разделе 3.6 примеры иллюстрируют методику получения                z-преобразования для некоторых простейших функций. Аналогичным способом составляются таблицы, содержащие наиболее часто употребляемые функции. Таблицы такого рода помещены в книгах, посвященных теории автоматического управления. В них для непрерывных функций времени даны преобразования Лапласа и z-преобразования.

Теоремы z-преобразования. Ниже приведены некоторые важнейшие теоремы, используемые при вычислении z-преобразований. Вывод этих теорем можно найти в книгах, перечисленных в списке литературы.

а). Линейность

б). Сдвиг по времени вправо

    d ³ 0.

в). Сдвиг по времени влево

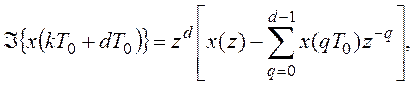   d ³ 0.

г). Изменение масштаба по временной координате z

.

д). Начальное значение

е). Конечное значение

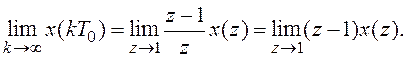
Обратное z-преобразование. В отличие от преобразования Лапласа, для которого прямой и обратный переходы x(t) ® x(s) и x(s) ® x(t)выполняются однозначно,            z-преобразование x(t) ® x(z) и обратное z-преобразование x(z) ® x(t)  не обладают этим свойством. Объясняется это тем, что они не учитывают поведения функции x(t) в промежутках между моментами срабатывания квантователя. В то же время преобразование x(kT₀) ® x(z) и обратное преобразова­ние x(z) ® x(kT₀)- взаимно однозначны.

На практике обратное z-преобразование вычисляют, записывая функцию x(z) как сумму элементарных членов, содержащихся в таблицах z-преобразований.

3.5. Дискретная передаточная функция

Предположим, что квантователь стоит на входе линейной системы с передаточной функцией W(s) или переходной функцией g(t), как показано на рисунке 3.9. Импульсный входной сигнал, поступающий в систему, описывается выражением

Учитывая, что переходная функция g(t) определяет реакцию системы на единичный импульс d(t), ее выходной сигнал выражается суммой свертки: