|
|
(3.13) |
Если квантование входного и выходного сигналов осуществляется синхронно, при t = nT0 имеем
|
|
(3.14) |
Для того чтобы получить преобразование Лапласа импульсного сигнала на выходе системы, воспользуемся уравнением
|
|
(3.15) |
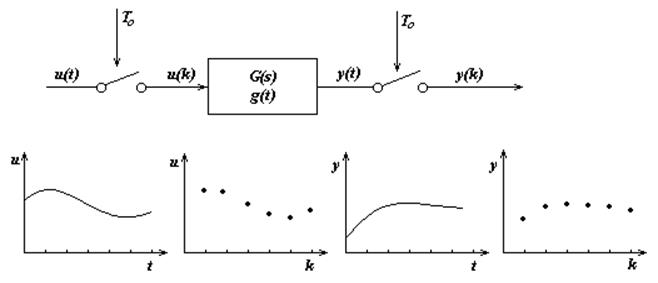
Рис. 3.9.
Подставим в эту формулу q = n - k:
|
|
(3.16) |
Отсюда дискретную передаточную функцию можно определить как
|
|
(3.17) |
Переходя
к переменной ![]() введем также
дискретную передаточную функцию по переменной z:
введем также
дискретную передаточную функцию по переменной z:
|
|
(3.18) |
Вычислениедискретных передаточных функций иллюстрируется двумя примерами.
Динамические свойства линейной стационарной системы с сосредоточенными параметрами полностью определяются его дифференциальным уравнением, имеющим вид
|
amy(m)(t) + am-1y(m-1)(t) + ... + a1y(t) + y(t) = bmu(m)(t) + bm-1u(m-1)(t) + ... + b1u(t) + b0u(t). |
(3.19) |
Применяя к этому уравнению преобразование Лапласа, получаем передаточную функцию по s:
|
|
(3.20) |
Аналогичным образом, имея разностное уравнение
|
y(k) + a1y(k - 1) + ... + amy(k - m) = = b0u(k) + b1u(k - 1) + ... + bmu(k - m), |
(3.21) |
можно построить дискретную передаточную функцию, используя теорему о сдвиге вправо:
|
|
(3.21) |
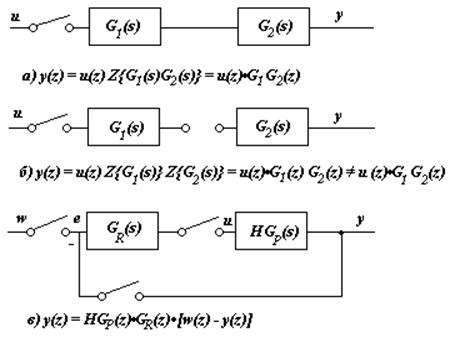
Рис. 3.10.
Последовательное соединение подсистем. При вычислении дискретной передаточной функции для совокупности линейных подсистем, соединенных последовательно, сначала следует объединить подсистемы, между которыми нет квантователей, и получить их передаточные функции. Далее эти передаточные функции перемножаются. Указанное правило поясняется примерами, представленными на рисунке 3.10.
Пример 3.1.В результате квантования непрерывная операция интегрирования
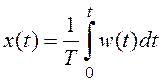
выполняется численно путем аппроксимации w(t) ступенчатой функцией. При этом интеграл заменяется суммой
![]()
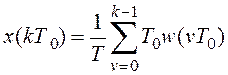 .
.
Поскольку x(kT0) зависит от второй дискретной функции, т. е.
![]() ,
,
результат записывается в неявной форме.
Неявную функцию можно представить в виде разностного уравнения. В частности, из полученного выражения следует, что
![]()
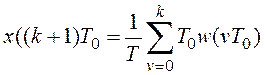 .
.
После вычитания имеем

или
![]() .
.
Уменьшив k на 1, приходим к окончательному соотношению
![]() ,
,
где a1 = – 1; b1 = T0/T. Это – линейное разностное уравнение первого порядка.
Пример 3.2. Дифференциальное уравнение апериодического звена имеет вид
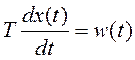 .
.
Заменяя дифференциал левой разностью, полученной при шаге квантования T0, имеем выражение
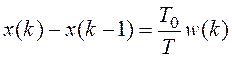 .
.
Если для дискретизации применяется правая разность
![]() ,
,
то получается то же уравнение, что и в примере 3.1:
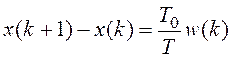 .
.
Пример 3.3.Дана ступенчатая функция: x(kT0) = 1(kT0), k = 0, 1, ... . В соответствии с определением (3.11) z-преобразование для этой функции имеет вид
x(z) = 1 + z-1 + z-2 + ... .
Сумму полученной бесконечной геометрической прогрессии можно записать в явной форме:
![]()
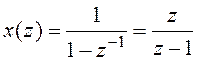 , если êzê>1.
, если êzê>1.
Пример
3.4.Для
экспоненциальной функции x(kT0) = e-akto (а
- действительное число, ![]() >1)
>1)
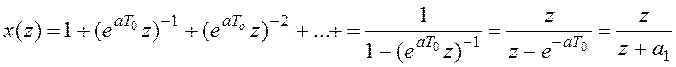 .
.
Пример 3.5.Дана синусоидальная функция: x(kT0) = sin w1kT0 . Записав эту функцию в виде
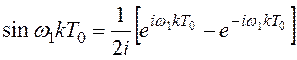 ,
,
используем результат предыдущего примера при a = iw1(или a = - iw1):
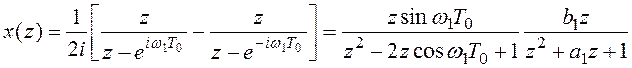 .
.
Пример 3.6. Апериодическое звено без экстраполятора на входе. Апериодическое звено с передаточной функцией
|
|
(3.22) |
где, a = 1/T, K¢ = K/T имеет импульсную переходную функцию
g(t) = K¢×e-at.
Подставим в это выражение t = kT0:
![]()
Используя определение (3.18) и результат примера 3.5, получим дискретную передаточную функцию
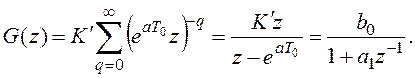
Вычислим параметры этой передаточной функции при K = 1, T = 7,5 c, T0 = 4c:
b0 = K¢ = K/T = 0,1333; a1 = - ![]() = - 0,5866.
= - 0,5866.
Описанное выше преобразование можно условно выразить как переход
![]()
Символ
![]() подразумевает,
что функция x(z),
соответствующая x(s), отыскивается
непосредственно по таблице z-преобразований. Так, можем записать
подразумевает,
что функция x(z),
соответствующая x(s), отыскивается
непосредственно по таблице z-преобразований. Так, можем записать
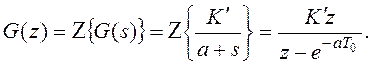
Пример 3.7. Если на входе непрерывной системы стоит экстраполятор нулевого порядка, как показано на рисунке 3.11, дискретная передаточная функция импульсной системы меняется:
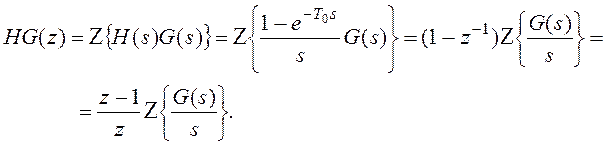
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.