Учебно-методический комплекс по дисциплине «Теоретические основы автоматизированного управления», страница 45

Вычисление передаточной функции одноконтурной системы. Замкнутую систему (структурную схему) называют одноконтурной, если при ее размыкании в какой-либо точке  получается цепочка из последовательно соединенных звеньев или цепь, не содержащая параллельных и обратных связей. Рассмотрим одноконтурную систему, приведенную на рисунке 2.12. Найдем передаточную функцию по входу g и выходу y. Участок по ходу сигнала от точки приложения входного воздействия до точки съема выходного сигнала назовем прямой цепью (рис. 2.12, а), а цепь из последовательно соединенных звеньев, входящих в замкнутый контур (рис. 2.12,б), - разомкнутой цепью. Как легко проверить, справедливо следующее правило:

передаточная функция одноконтурной системы с отрицательной (положительной) обратной связью равна передаточной функции прямой цепи, деленной на единицу плюс (минус) передаточная функция разомкнутой цепи:

W_yg =

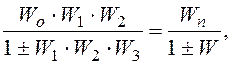
где W_n - передаточная функция прямой цепи, W - передаточная функция разомкнутой цепи. Сформулированное правило справедливо для любой одноконтурной системы.

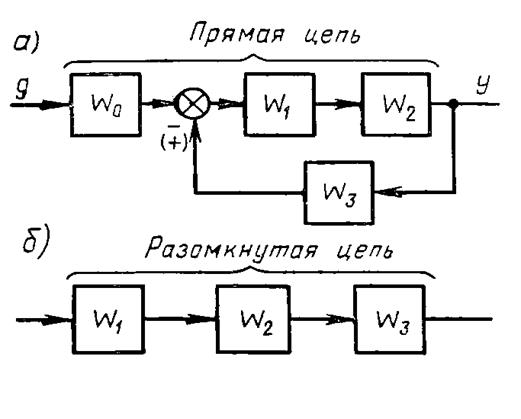
Рис. 2.12.

Вычисление передаточной функции многоконтурной системы.Замкнутую систему (структурную схему) называют многоконтурной, если при ее размыкании получается цепь, содержащая параллельные или обратные связи, или, иначе, замкнутую систему называют многоконтурной, если она помимо главной обратной связи содержит местные обратные или параллельные связи. Говорят, что многоконтурная система имеет перекрещивание связи, если контур обратной или параллельной связи охватывает участок цепи обратной или параллельной связи. Для вычисления передаточной функции многоконтурной системы необходимо прежде всего перестановкой и переносом узлов и сумматоров освободиться от перекрещивающихся связей. Затем, используя первые три правила преобразования структурных схем, преобразовать ее в одноконтурную систему, передаточную функцию которой легко вычислить согласно сформулированному выше правилу. При этом следует помнить, что при преобразовании структурной схемы нельзя переносить сумматор через точку съема выходного сигнала, так как при этом точка съема оказывается на неэквивалентном участке линии связи.

2.9. Примеры и задачи

Пример 2.1. Математическое описание колебательного звена. Колебательное звено имеет передаточную функцию вида

где:

 T- постоянная времени;

x- коэффициент демпфирования;

 k - передаточный коэффициент.

Графики переходной функции колебательного звена изображены на рисунке 2.13. Для устойчивого колебательного звена 0 < x < 1. Если x×k > 1, то звено может быть представлено в виде двух апериодических звеньев с постоянными времени Т₁ и Т₂; если x= 1, то апериодические звенья имеют одинаковую постоянную времени, т.е. Т₁ = Т₂.

Когда коэффициент x < 0, то выходные колебания с течением времени возрастают. Такое звено является неустойчивым колебательным звеном.

Пример 2.2.Найдем  передаточные  функции  системы,  изображенной  на  рисун-ке 2.14, а, по “входам ” g и f и “выходам” y и e. Эта система является многоконтурной с прекращающимися связями. Перенеся и переставив сумматоры, ее можно привести к многоконтурной  системе без перекрещивающихся связей (рис. 2.14, б). После замены параллельно соединенных звеньев и звена, охваченного обратной связью, эквивалентными звеньями с передаточными функциями W₁₃ = W₁ + W₃,  W₂₄ = W₂/(1 - W₂×W₄) получим одноконтурную схему (рис. 2.14, в).

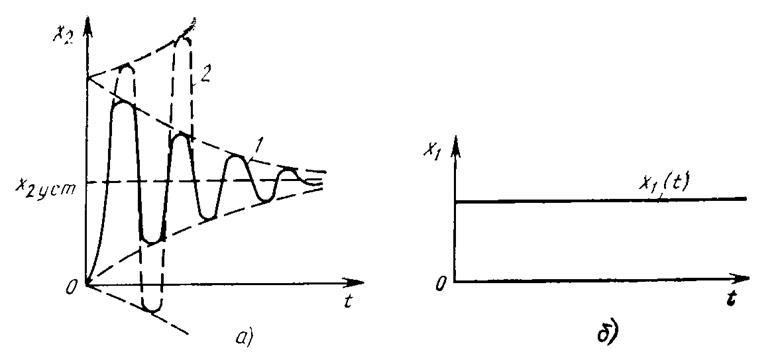
Рис. 2.13.

При вычислении функции по входному воздействию g полагаем f = 0. Согласно правилу вычисления передаточной функции одноконтурных систем, имеем

W_yg =

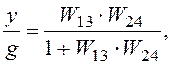
W_eg =

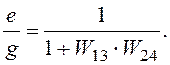
При вычислении передаточной функции по входному воздействию f полагаем g = 0. При этом сравнивающее звено становится инвертирующим звеном с передаточной функцией, равной (- 1). Инвертирующее звено в замкнутый контур можно не вводить, если суммирующее звено преобразовать в сравнивающее звено. Поэтому в данном случае структурную схему можно представить так, как это показано на рисунке 2.14, г.

Из этой схемы видно